[Python] 360度パノラマ画像の平面展開
360度画像 (パノラマ画像, Equirectangular) を平面に展開する方法を解説し、Pythonの実装を掲載する。
関連
- 3Dから2Dへの投影
- 3Dから2Dへの投影 - 射影法
- [Python] 360度パノラマ画像の平面展開 (本投稿)
目次
仕組み
Equirectangular
ここでは360度カメラの保存形式の一つであるEquirectangular形式の画像を取り扱う。
Equirectangularの画像の各ピクセルは、カメラに届いく光の球面座標の角度に相当する。
次の右手系の球面座標\((r, \theta, \phi)\)に対して、画像の縦軸(上から下)が\(\theta\in[0, \pi]\)、画像の横軸(右から左)が\(\phi\in[0, 2\pi)\)に対応している。
\begin{align} \left\{ \begin{array}{ll} X &= r\sin(\theta)\cos(\phi), \\ Y &= r\sin(\theta)\sin(\phi), \\ Z &= r\cos(\theta). \\ \end{array} \right. \end{align}
空間の中でカメラが光を感知することは、色の付いた単位球面を内側の中心から見ることと同じことである。

Equirectangular画像を貼り付けた球面
マッピングの算出
OpenCVのcv2.remap関数を用いることを前提に話を進める。
cv2.remapでは、「出力画像のピクセル座標」⇒「入力画像のピクセル座標」の対応を表す2次元配列を引数に与えることで、画像の幾何変換を行うことができる。
ここでは、出力画像の各ピクセル位置\((i,j)\)から、入力画像 (Equirectangular) の各ピクセル位置\((s,t)\)を求めることによって360度画像の平面展開を実装する。
画角によるスケーリング
まずは、出力画像の各ピクセル座標\((i,j)\)を\(Z=1\)平面に射影する。
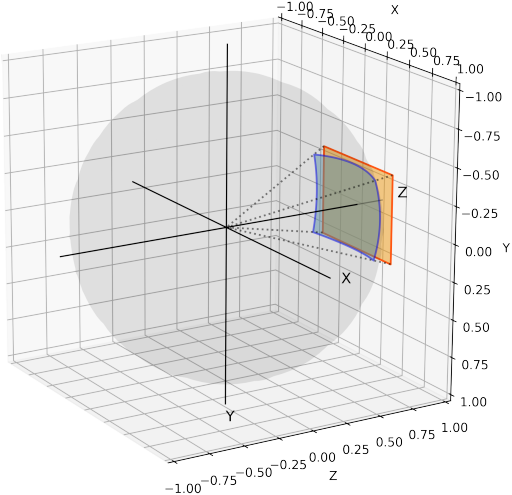
\(Z=1\)平面への射影 (橙の平面に合うようにスケーリングする)
\(Z=1\)平面に射影された画像の大きさを知るためには、画角 (FOV) を用いる必要がある。(FOVは外部パラメーターとして実行時に別途渡さなければならない)
例えば、対角画角かつ透視投影の場合は
\begin{align*} \tan\left(\frac{\text{FOV}}{2}\right) = \frac{\sqrt{w^2+h^2}}{2} \end{align*}
となるように画像の大きさ\((w,h)\)を伸縮させる。\(\tan(\cdot)\)の部分は射影方式によって異なり、適用させたいものを選ぶ必要がある。
- 透視投影 : \(r\left(\frac{\text{FOV}}{2}\right) = \tan\left(\frac{\text{FOV}}{2}\right)\)
- 立体射影 : \(r\left(\frac{\text{FOV}}{2}\right) = 2\tan\left(\frac{\text{FOV}}{4}\right)\)
- 等距離射影 : \(r\left(\frac{\text{FOV}}{2}\right) = \frac{\text{FOV}}{2}\)
- 等立体角射影 : \(r\left(\frac{\text{FOV}}{2}\right) = 2\sin\left(\frac{\text{FOV}}{4}\right)\)
- 正射影 : \(r\left(\frac{\text{FOV}}{2}\right) = \sin\left(\frac{\text{FOV}}{2}\right)\)
次の実装では、倍率\(a\)を計算することにより伸縮後の画像の大きさの半分に相当する値\((\text{vw}, \text{vh})\)を求めている。
また、この値を求めた後に、これから変換していく二次元配列を初期化している。xは\(Z=1\)平面での\(X\)座標の配列、yは\(Y\)座標の配列を意味する。
# 像の範囲を求める
if fov_mode:
# fovが視野角を意味するモード
# 視野角fovから(像の対角線の長さ)/2=r(fov/2)に変換
fov = self.r(fov / 2, mapping_style=mapping_style)
a = fov / np.sqrt(width ** 2 + height ** 2)
vw = width * a # z=1平面上の幅の半分
vh = height * a
# 画像の座標(i, j)から像の中の座標への対応
x = np.tile(np.linspace(-vw, vw, width), [height, 1])
y = np.tile(np.linspace(-vh, vh, height), [width, 1]).T
球面への射影
次に各値を球面上に射影する。
今持っている\(X,Y\)の値は、画像の座標を伸縮させたものに過ぎないので、射影方式を考慮して角度を計算してから球面上の座標を求める必要がある。
具体的には、\(\sqrt{X^2+Y^2}\)を各射影方式の\(r\)の逆関数\(r^{-1}\)に作用させて中心からの角度
\begin{align*} \alpha=r^{-1}\left(\sqrt{X^2+Y^2}\right) \end{align*}
を得て、
\begin{align*} a2 := \frac{\sin(\alpha)}{\sqrt{X^2+Y^2}} \end{align*}
で\(X,Y\)をスケーリングすることで、球面上の\(X,Y\)座標が得られる。\(Z\)座標は\(Z=\sqrt{1-X^2-Y^2}\)から求めれば良い。
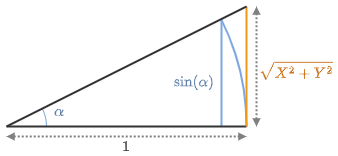
射影方式の反映 (透視投影の場合)
# 球面上の座標に変換するための倍率を計算
# self._r_inv(a2) が像の中心からの角度になっている
a2 = np.sqrt(x ** 2 + y ** 2)
a2 = np.sin(self.r_inv(a2, mapping_style=mapping_style)) / a2
# 球面上の座標(x, y, z)を求める
x *= a2
y *= a2
z = np.sqrt(1 - x ** 2 - y ** 2)
return np.stack((x, y, z), axis=2) # shape = height, width, 3
カメラの視点に向けて回転
次はカメラの方向を反映させる。
カメラが球面の\((\text{lon}_C, \text{lat}_C)\)方向を向いているとする。
この時点の\((X,Y,Z)\)は\((X,Y,Z)=(0,0,1)\)を中心とした値を取るので、その中心がカメラの方向と一致するように回転させれば良い。
まずは、\(Z\)軸から\(Y\)軸方向へ\(\frac{\pi}{2}-\text{lat}_C\)回転させる。
\begin{align*} \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} \leftarrow \begin{pmatrix} 1 & 0 & 0 \\ 0 & \sin(\text{lat}_C) & \cos(\text{lat}_C) \\ 0 & -\cos(\text{lat}_C)& \sin(\text{lat}_C) \end{pmatrix}\begin{pmatrix} X \\ Y \\ Z \end{pmatrix} \end{align*}
次に、\(Y\)軸方向から\(X\)軸方向へ\(\frac{\pi}{2}-\text{lon}_C\)回転させる。
\begin{align*} \begin{pmatrix} X \\ Y \\ Z \end{pmatrix} \leftarrow \begin{pmatrix} \sin(\text{lon}_C) & \cos(\text{lon}_C) & 0 \\ -\cos(\text{lon}_C)& \sin(\text{lon}_C) & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X \\ Y \\ Z \end{pmatrix} \end{align*}
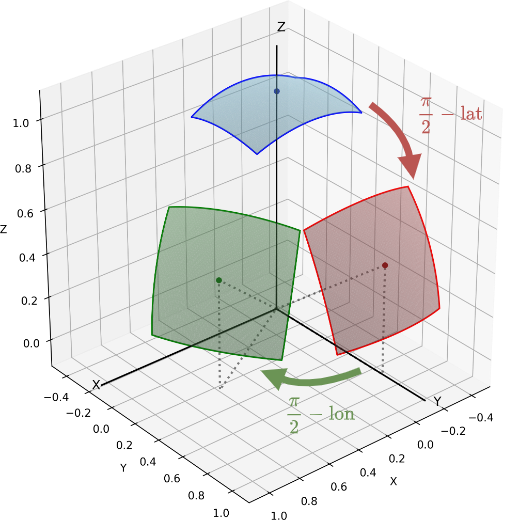
カメラの視点に向けて回転
# x軸周りに -(pi/2-lat) 回転
rx = np.array([[1, 0, 0],
[0, np.sin(lat), np.cos(lat)],
[0, -np.cos(lat), np.sin(lat)]])
# z軸周りに -(pi/2-lon) 回転
rz = np.array([[np.sin(lon), np.cos(lon), 0],
[-np.cos(lon), np.sin(lon), 0],
[0, 0, 1]])
xyz = xyz.reshape([height * width, 3]).T
xyz = np.dot(rx, xyz)
xyz = np.dot(rz, xyz)
角度の算出
球面上の\(X,Y,Z\)座標が得られたので、この値から球面上の角度を算出する。
\begin{align*} \left\{ \begin{array}{ll} X &= \sin(\theta)\cos(\phi) \\ Y &= \sin(\theta)\sin(\phi) \\ Z &= \cos(\theta) \\ \end{array} \right. \end{align*}
の関係から、
\begin{align*} \left\{ \begin{array}{ll} \phi &= \text{arctan2}(Y, X) \\ \theta &= \frac{\pi}{2}-\arcsin(Z) \end{array} \right. \end{align*}
と求めることができる。
実装では、
\begin{align*} \left\{ \begin{array}{ll} \text{lon}&=\phi&\in(-\pi,\pi] \\ \text{lat}&=\frac{\pi}{2}-\theta&\in[-\pi/2,\pi/2] \end{array} \right. \end{align*}
を計算して用いている。
# 球面上の座標(x, y, z)を緯度lonと経度latに変換する
lon_map = np.arctan2(xyz[1], xyz[0]) # 東経
lat_map = np.arcsin(xyz[2]) # 北緯
lon_map = lon_map.reshape([height, width])
lat_map = lat_map.reshape([height, width])
Equirectangularのピクセル位置の算出
最後に、求めた角度からEquirectangular画像におけるピクセル位置\((s,t)\)を算出する。
Equirectangular画像は、上から下へ\(\text{lat}\)が減少し、右から左へ\(\text{lon}\)が増加する仕様なので、大きさを\((W,H)\)としたとき、
\begin{align*} s &= W\left(\frac{1}{2} - \frac{\text{lon}}{2\pi}\right) \\ t &= H\left(\frac{1}{2} - \frac{\text{lat}}{\pi}\right) \\ \end{align*}
とすることでピクセル座標を求められる。
この式は、\((\text{lon},\text{lat})=(0,0)\)のときに、Equirectangular画像の中心\(\left(\frac{W}{2},\frac{H}{2}\right)\)に相当する位置が対応するように設定されている。
i = panorama_width * (1 / 2 - spmap[0] / 2 / np.pi)
j = panorama_height * (1 / 2 - spmap[1] / np.pi)
実装
機能
平面展開 (__call__)
360度画像の指定方向の像をこれまで解説した方法で作り、画像ファイルに出力する。
逆展開 (inverse)
平面展開の逆で、平面展開された画像と同じサイズのレイヤー(透過pngを想定)を読み込み、元の360度画像に重なる形で引き戻す。このようにすることで、展開画像に描画した線などの情報を、元の360度画像に反映させることができる。
考え方は簡単で、平面展開の逆を行うだけ。最初に球面上の座標 (X, Y, Z)がわかり、最後にレイヤー上の座標 (x, y)が求められる。途中、視界の裏側の点を一様に無限遠点に取るという操作で不要な範囲を取り除いている。(具体的にはソースコードを読んでほしい)
ソースコード
必要なpythonパッケージと360度画像は各自手に入れてほしい。360度画像はEquirectangularと検索すれば様々なものが入手できる。
from abc import ABCMeta, abstractmethod
import tkinter
import tkinter.filedialog
import numpy as np
import cv2
class PanoramaProjector(metaclass=ABCMeta):
@staticmethod
def parse_mapping_style(mapping_style):
mode = 1
if isinstance(mapping_style, str):
if mapping_style == 'perspective':
mode = 1
elif mapping_style == 'stereographic':
mode = 1 / 2
elif mapping_style == 'equidistant':
mode = 0
elif mapping_style == 'equisolid_angle':
mode = -1 / 2
elif mapping_style == 'orthographic':
mode = -1
elif isinstance(mapping_style, tuple):
f, n = mapping_style
if f == 'tan':
mode = 1 / n
elif f == 'id':
mode = 0
elif f == 'sin':
mode = -1 / n
else:
mode = mapping_style
return mode
def __call__(self, panorama, lon=0, lat=0, fov=105, width=800, height=600, mapping_style=1, fov_mode=True):
lon = np.radians(lon)
lat = np.radians(lat)
if fov_mode:
fov = np.radians(fov)
[panorama_height, panorama_width, _] = panorama.shape
spmap = self._spmap(lon, lat, fov, width, height, mapping_style=mapping_style, fov_mode=fov_mode)
pxmap = self._pxmap(spmap, panorama_width, panorama_height)
return cv2.remap(panorama,
pxmap[0].astype(np.float32),
pxmap[1].astype(np.float32),
cv2.INTER_CUBIC,
borderMode=cv2.BORDER_WRAP,
)
@staticmethod
def r(angle, mapping_style=1):
# projection fomula of distance
if mapping_style == 0:
return angle
elif mapping_style > 0:
return np.tan(mapping_style * angle) / mapping_style
else:
return np.sin(mapping_style * angle) / mapping_style
@staticmethod
def r_inv(d, mapping_style=1):
if mapping_style == 0:
inv = d
elif mapping_style > 0:
inv = np.arctan(mapping_style * d) / mapping_style
else:
inv = np.arcsin(mapping_style * d) / mapping_style
if isinstance(inv, np.ndarray):
inv[inv > np.pi / 2] = np.float('inf')
return inv
def _spmap(self, lon, lat, fov, width, height, mapping_style=1, fov_mode=True):
xyz = self._3dmap(fov, width, height, mapping_style=mapping_style, fov_mode=fov_mode)
# x軸周りに -(pi/2-lat) 回転
rx = np.array([[1, 0, 0],
[0, np.sin(lat), np.cos(lat)],
[0, -np.cos(lat), np.sin(lat)]])
# z軸周りに -(pi/2-lon) 回転
rz = np.array([[np.sin(lon), np.cos(lon), 0],
[-np.cos(lon), np.sin(lon), 0],
[0, 0, 1]])
xyz = xyz.reshape([height * width, 3]).T
xyz = np.dot(rx, xyz)
xyz = np.dot(rz, xyz)
# 球面上の座標(x, y, z)を緯度lonと経度latに変換する
lon_map = np.arctan2(xyz[1], xyz[0]) # 東経
lat_map = np.arcsin(xyz[2]) # 北緯
lon_map = lon_map.reshape([height, width])
lat_map = lat_map.reshape([height, width])
return lon_map, lat_map
def _3dmap(self, fov, width, height, mapping_style=1, fov_mode=True):
# 画像の座標(i, j)から回転前の球面上の座標(x, y, z)への対応を作る
# 像の範囲を求める
if fov_mode:
# fovが視野角を意味するモード
# 視野角fovから(像の対角線の長さ)/2=r(fov/2)に変換
fov = self.r(fov / 2, mapping_style=mapping_style)
a = fov / np.sqrt(width ** 2 + height ** 2)
vw = width * a # z=1平面上の幅の半分
vh = height * a
# 画像の座標(i, j)から像の中の座標への対応
x = np.tile(np.linspace(-vw, vw, width), [height, 1])
y = np.tile(np.linspace(-vh, vh, height), [width, 1]).T
# 球面上の座標に変換するための倍率を計算
# self._r_inv(a2) が像の中心からの角度になっている
a2 = np.sqrt(x ** 2 + y ** 2)
a2 = np.sin(self.r_inv(a2, mapping_style=mapping_style)) / a2
# 球面上の座標(x, y, z)を求める
x *= a2
y *= a2
z = np.sqrt(1 - x ** 2 - y ** 2)
return np.stack((x, y, z), axis=2) # shape = height, width, 3
@abstractmethod
def _pxmap(self, sperical_map, panorama_width, panorama_height):
pass
def inverse(self, perspective, lon=0, lat=0, fov=105, panorama_width=8192, panorama_height=4096,
mapping_style=1, fov_mode=True):
lon = np.radians(lon)
lat = np.radians(lat)
if fov_mode:
fov = np.radians(fov)
[height, width, _] = perspective.shape
pxmap_inv = self._pxmap_inv(panorama_width, panorama_height)
x, y = self._spmap_inv(pxmap_inv, lon, lat, fov, width, height,
mapping_style=mapping_style, fov_mode=fov_mode)
panorama = cv2.remap(perspective,
x.astype(np.float32),
y.astype(np.float32),
cv2.INTER_CUBIC,
borderMode=cv2.BORDER_TRANSPARENT)
return panorama
def _spmap_inv(self, pxmap_inv, lon, lat, fov, width, height, mapping_style=1, fov_mode=True):
xyz, panorama_width, panorama_height = self._3dmap_inv(pxmap_inv, lon, lat)
if fov_mode:
fov = self.r(fov / 2, mapping_style=mapping_style)
a = fov / np.sqrt(width ** 2 + height ** 2)
vw = width * a
vh = height * a
# 裏側を取り除く
f = xyz[2] <= 0 # filter
xyz[:, f] = [[float('inf')], [float('inf')], [-1]]
a2 = self.r(np.arccos(xyz[2]), mapping_style=mapping_style) / np.sqrt(xyz[0] ** 2 + xyz[1] ** 2)
xyz *= a2
xyz[0] += vw
xyz[1] += vh
xyz /= a*2
x = xyz[0].reshape([panorama_height, panorama_width])
y = xyz[1].reshape([panorama_height, panorama_width])
return x, y
def _3dmap_inv(self, pxmap_inv, lon, lat):
lon_map, lat_map = pxmap_inv
panorama_height = lon_map.shape[0]
panorama_width = lat_map.shape[1]
# x = sin(pi/2 - lat) * cos(lon) = cos(lat) * cos(lon)
# y = sin(pi/2 - lat) * sin(lon) = cos(lat) * sin(lon)
# z = cos(pi/2 - lat) = sin(lat)
x = np.cos(lat_map) * np.cos(lon_map)
y = np.cos(lat_map) * np.sin(lon_map)
z = np.sin(lat_map)
xyz = np.stack((x, y, z), axis=2)
# x軸周りに (pi/2-lat) 回転
rxi = np.array([[1, 0, 0],
[0, np.sin(lat), -np.cos(lat)],
[0, np.cos(lat), np.sin(lat)]])
# z軸周りに (pi/2-lon) 回転
rzi = np.array([[np.sin(lon), -np.cos(lon), 0],
[np.cos(lon), np.sin(lon), 0],
[ 0, 0, 1]])
xyz = xyz.reshape([panorama_height * panorama_width, 3]).T
xyz = np.dot(rzi, xyz)
xyz = np.dot(rxi, xyz)
return xyz, panorama_width, panorama_height
@abstractmethod
def _pxmap_inv(self, panorama_width, panorama_height):
pass
# equirectangular
class EquirecProjector(PanoramaProjector):
def _pxmap(self, spmap, panorama_width, panorama_height):
i = panorama_width * (1 / 2 - spmap[0] / 2 / np.pi)
j = panorama_height * (1 / 2 - spmap[1] / np.pi)
return i, j
def _pxmap_inv(self, width, height):
lon_map = np.tile(np.linspace(np.pi, -np.pi, width), [height, 1])
lat_map = np.tile(np.linspace(np.pi/2, -np.pi/2, height), [width, 1]).T
return lon_map, lat_map
class PanoramaViewer(metaclass=ABCMeta):
def __init__(self, image_path, projector, lon=0, lat=0, fov=105, width=800, height=600, mapping_style='perspective'):
self._image = cv2.imread(image_path, cv2.IMREAD_COLOR)
self._projector = projector
self._lon = lon
self._lat = lat
self._width = width
self._height = height
self._mapping_style = projector.parse_mapping_style(mapping_style)
self._d = self._projector.r(np.radians(fov) / 2, mapping_style=self._mapping_style)
self._stride = np.degrees(self._projector.r_inv(self._d / 10))
def __call__(self):
if self._mapping_style > 0:
p = 1 - np.cos(self._mapping_style * np.pi / 2)
elif self._mapping_style < 0:
p = -1 + np.cos(self._mapping_style * np.pi / 2)
else:
p = 0
# f:p -> style
# arccosに従って滑らかに遷移させる
def f(p):
if p > 0:
return 2 / np.pi * np.arccos(1 - p)
elif p < 0:
return -2 / np.pi * np.arccos(1 + p)
else:
return 0
while True:
image = self._projector(self._image, self._lon, self._lat, self._d, self._width, self._height,
mapping_style=self._mapping_style, fov_mode=False)
cv2.imshow("image", image)
key = cv2.waitKeyEx(0)
if key == 2424832: # left
self._lon += self._stride
elif key == 2490368: # up
self._lat += self._stride
if self._lat > 90:
self._lat = 90
elif key == 2555904: # right
self._lon -= self._stride
elif key == 2621440: # down
self._lat -= self._stride
if self._lat < -90:
self._lat = -90
elif key == ord('z'):
self._d /= 1.1
self._stride = np.degrees(self._projector.r_inv(self._d / 10))
elif key == ord('x'):
self._d *= 1.1
self._stride = np.degrees(self._projector.r_inv(self._d / 10))
elif key == ord('m'):
p -= 0.1
if p < -1:
p = -1
self._mapping_style = f(p)
elif key == ord('n'):
p += 0.1
if p > 1:
p = 1
self._mapping_style = f(p)
elif key == ord('s'):
self.output(image=image)
elif key == ord('i'):
root = tkinter.Tk()
root.withdraw()
layer_path = tkinter.filedialog.askopenfilename(filetypes=[('PNG', '*.png')])
if layer_path is not '':
self.inverse(layer_path)
elif cv2.getWindowProperty('img', cv2.WND_PROP_AUTOSIZE) == -1:
cv2.destroyAllWindows()
return
def output(self, image=None, filename=None):
if image is None:
mapping_style = self._projector.parse_mapping_style(self._mapping_style)
image = self._projector(self._image, self._lon, self._lat, self._d, self._width, self._height,
mapping_style=mapping_style, fov_mode=False)
if filename is None:
filename = 'save/{}_{}_{}_{}_{}.jpg'.format(self._lon, self._lat, self._d, self._width, self._height)
cv2.imwrite(filename, image)
def inverse(self, layer_path, image=None, filename=None):
if image is None:
perspective = cv2.imread(layer_path, cv2.IMREAD_UNCHANGED)
[panorama_height, panorama_width, _] = self._image.shape
mapping_style = self._projector.parse_mapping_style(self._mapping_style)
image = self._projector.inverse(
perspective, self._lon, self._lat, self._d, panorama_width, panorama_height,
mapping_style=mapping_style, fov_mode=False)
if filename is None:
filename = 'save/{}_{}_{}_{}_{}.png'.format(self._lon, self._lat, self._d, self._width, self._height)
cv2.imwrite(filename, image)
if __name__ == '__main__':
projector = EquirecProjector()
viewer = PanoramaViewer('resource/panorama.png', projector)
viewer()
