360度画像の平面展開
概要
360度カメラ(全天球カメラ)に限らず、カメラは通常広い空間の一点にしか存在しないので、風景を撮影しようとしたときに空間的な情報を全て捉えられるわけではなく、カメラに届く各立体角の光(色)を様々な種類のレンズを通してイメージセンサーに当てることで保存することしかできない。
立体角は2次元しかないので、保存された画像から元の3次元の情報を復元することはできない。つまり、カメラから見た角度を保存することはできても、深さ(カメラからの距離)に関する情報は保存することができない。
そのような2次元の情報を紙やモニターに射影することで表現する5つの方法について調べたことをまとめる。
目次
Equirectangular
ここでは360度カメラの保存形式の一つであるEquirectangular形式の画像を取り扱う。
以下の右手系の球面座標\((r, \theta, \phi)\)に対して、画像の縦軸(上から下)が\(\theta\in[0, \pi]\)、画像の横軸(右から左)が\(\phi\in[0, 2\pi)\)に対応している。
\begin{align} \left\{ \begin{array}{ll} x &= r\sin(\theta)\cos(\phi), \\ y &= r\sin(\theta)\sin(\phi), \\ z &= r\cos(\theta). \\ \end{array} \right. \end{align}
空間の中でカメラが光を感知することは、色の付いた単位球面を内側の中心から見ることと同じことである。
射影方式
球面上の色情報を平面に射影する方式には主に以下の5種類がある。
- 透視投影 (Perspective projection)
- 立体射影 (Stereographic projection)
- 等距離射影 (Equidistant projection)
- 等立体角射影 (Equisolidangle projection)
- 正射影 (Orthographic projection)
透視投影を除く4種類はいわゆる魚眼で、中心が強調された像となる。
立体射影・等距離射影・正射影は全球を射影することができるが、透視投影と正射影は半球のみしか射影できない。
透視投影 (中心射影, Perspective projection)
透視投影は、いわゆる普通に写真を撮るときの基本的な射影方式。
球面の奥に仮想の平面を見立てて、カメラは着色された平面から来た光を立体角ごとに感知していると考える。射影された平面が平面展開の結果そのものとなる。
撮影の対象となる3次元空間上の直線が展開結果でも直線となるという性質があり、自然な見た目となる。
ある点の視野中心からの角度を\(\theta\)とすると、その点に対応する展開結果の点と中心との距離\(r\)は以下のように表される。
\begin{align} r = \tan(\theta) \end{align}
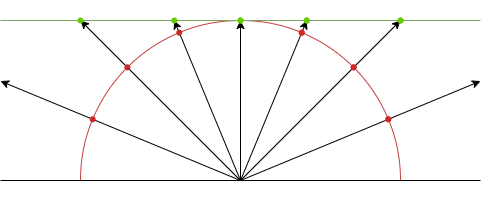
対角線視野135°の展開例
立体射影 (極射影, ステレオ投影, Stereographic projection)
立体射影では、平面と接していない側の極を中心に球面上の各点を平面へと射影する。
4つの魚眼方式の中では透視投影に最も近く、直線の湾曲が穏やか。
地図の分野では「平射図法」と呼ばれる。
\begin{align} r = 2\tan\left(\frac{\theta}{2}\right) \end{align}
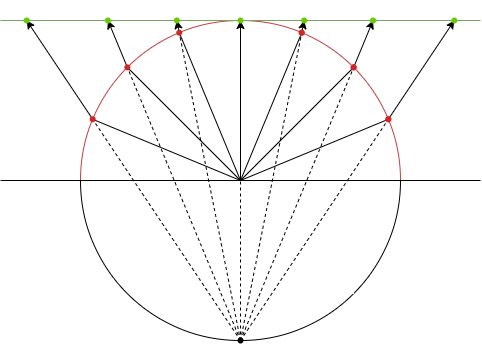
対角線視野135°の展開例
等距離射影 (Equidistant projection)
等距離射影では、展開結果の中心からの距離が球面の中心からの角度に比例するよう射影される。
展開結果画像上の距離で球面上の角度を調べることができるという利点がある。
地図の分野では「正距方位図法」と呼ばれる。
\begin{align} r = \theta \end{align}
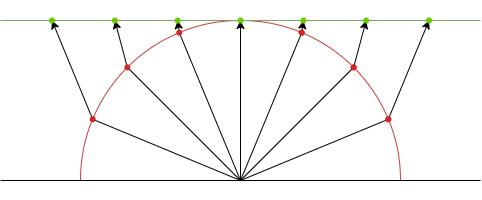
対角線視野135°の展開例
等立体角射影 (Equisolidangle projection)
等立体角射影では、展開結果の中心からの距離が球面の中心からの弧の長さに比例するよう射影される。
展開結果画像上の微小面積で球面上の微小立体角を近似することができるという性質がある。
地図の分野では「ランベルト正積方位図法」と呼ばれる。
\begin{align} r = 2\sin\left(\frac{\theta}{2}\right) \end{align}
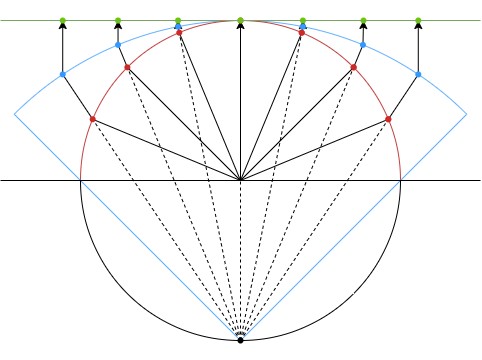
対角線視野135°の展開例
正射影 (Orthographic projection)
正射影では、球面上の各点が平面へ垂直に射影される。
地図の分野では「正射図法」と呼ばれる。
\begin{align} r = \sin(\theta) \end{align}
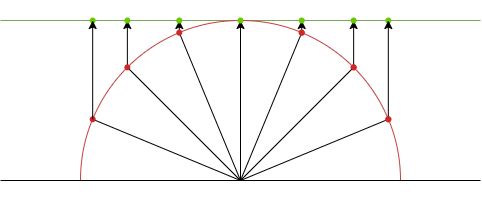
対角線視野135°の展開例