画像補間フィルター
この記事では画像リサイズで用いられる補間アルゴリズムを解説する。
各アルゴリズムでのリサイズの例は記事末尾に掲載。
目次
概要
\(p\in R^{I\times J}\)を\(q\in R^{K\times L}\)にリサイズすることを目的とする。
多くのアルゴリズムでは、まず\(p\)を連続な\(\tilde{p}\in R^{\left[-\frac{1}{2}, I-\frac{1}{2}\right]\times \left[-\frac{1}{2}, J-\frac{1}{2}\right]}\)に補間し、次に\(\tilde{p}\)から等間隔に\(K\times L\)個の値を取るという2段階でリサイズが実行される。
前半の連続補間に関してはこれまで様々な方法が生み出されており、アルゴリズムの違いによって画像のリサイズの結果に違いが発生する。この記事ではそれらの補間アルゴリズムについて解説する。
なお、この記事では添字は0から始まるものとする。
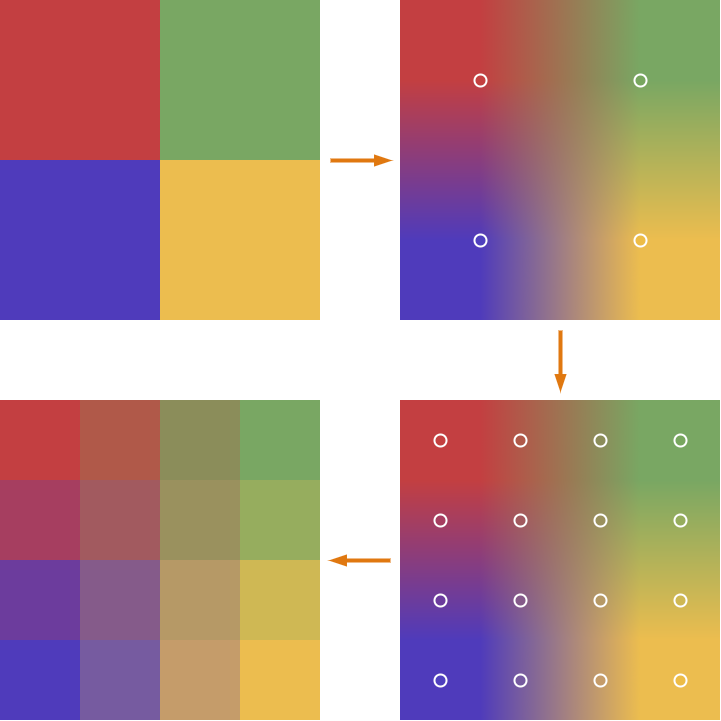
補間フィルター
多くの補間アルゴリズムは、補間前の離散な画素値と1次元の偶関数との畳み込みによって表すことができる。このような1次元の関数のことを補間フィルターあるいは補間カーネルと呼ぶ。
フィルター\(k\)によって表現される補間アルゴリズムでは、\(\tilde{p}\)は次のように計算することができる。
\begin{align} \tilde{p}(s,t) = \sum_{j=0}^{J-1} \sum_{i=0}^{I-1} k(s-i)k(t-j)p_{i,j} \end{align}
これは一度画像を横方向に補間してから、次に縦方向に補間することと同じである。(縦→横の順でも同じ)
\begin{align} \tilde{p}(s,t) = \sum_{j=0}^{J-1} k(t-j) \sum_{i=0}^{I-1} k(s-i)p_{i,j} \end{align}
フィルターについてはこの投稿で各種の具体例を提示しているので、そちらを見て理解してほしい。
正規性
色が一定の画像は補間した値も同じ色にならなければならないので、補間フィルター\(k\)には次の制約が課される。
\begin{align} 1 = \sum_{i=-\infty}^{\infty} k(s-i), \forall s\in [0,1] \tag{1} \end{align}
台の有界性
また計算処理の都合上、補間フィルターの台\(\mathrm{supp}(k)\)は有界区間であることが多い。
補間フィルターの台が\([-n, n]\)の場合、\(n\)を補間フィルターの半径と呼ぶ。
補間フィルターの半径に対して一定以上の縮小率で画像を縮小した場合、縮小結果は元の画像の情報を取りこぼす可能性がある。
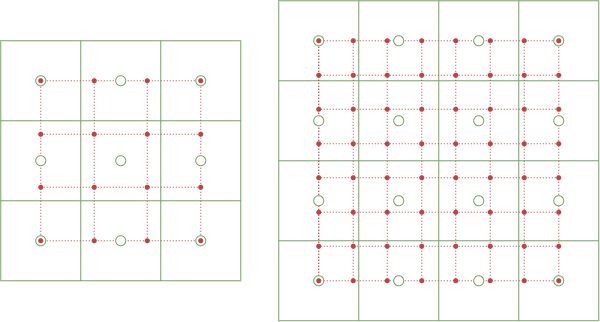
例えば以下の図では25x25の画像を3x3に縮小する場合を表しているが、補間フィルターの半径が4以下の場合、緑で塗った画素はどんな色であっても縮小結果には一切影響を与えない。

25x25→3x3に半径4のフィルターで縮小する場合
(緑の格子は縮小前画像の画素を表し、赤の点と破線は縮小後の画素を表す)
\(I\times J\)の画像を半径\(n\)のフィルターでを\(K\times L\)に縮小するとき、縮小結果に影響を与えない画素が存在する必要十分条件は以下。
\begin{align} &2nK+1 \leq I \land \\ &2nL+1 \leq J \end{align}
端の値の処理
上記のように、連続補間する際には周辺の何ピクセルか先の画素から色の値を取得しなければならない場合がある。
しかし、画像の端などでは必ずしも全ての必要な画素が存在するとは限らない。そのような場合は、画像の端の値を外側に外挿することによって周辺ピクセルとして利用するなどの処理が取られる。
外挿の具体的な実装として、例えばPyTorchでは端の値を繰り返す方法が採用されている。

align corners
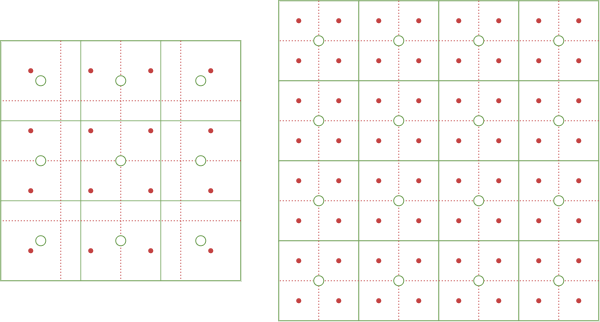
連続に補間した後、等間隔に\(K\times L\)個の値を取ることになるが、これには2つの方法がある。
align_corners=True
一つはリサイズ前後で角のピクセルが同じ位置を指すようにする方法。
角のピクセルが連続画像の同じ位置を指すので、リサイズ前後で角のピクセルの値が等しくなる。
しかし、画像の整数倍の拡大に対して拡大前後のピクセルの対応が不揃いになるという欠点もある。
\begin{align} q_{k,l} = \tilde{p}\left(\frac{I-1}{K-1}k, \frac{J-1}{L-1}l\right) \end{align}
3x3→4x4に拡大する場合と、4x4→8x8に拡大する場合
(緑はリサイズ前画像の画素位置で、赤はリサイズ後画像の画素位置)
align_corners=False
もう一つは連続画像の領域の端で合わせる方法。
前の方法の逆で、整数倍の拡大に対しては安定したパターンを持つ。
しかし、拡大後のピクセルは拡大前のピクセルより外側を参照するので、連続補間時の端の処理の影響を受けやすい。
\begin{align} q_{k,l} = \tilde{p}\left(\frac{I}{K}\left(k+\frac{1}{2}\right)-\frac{1}{2}, \frac{J}{L}\left(l+\frac{1}{2}\right)-\frac{1}{2}\right) \end{align}
3x3→4x4に拡大する場合と、4x4→8x8に拡大する場合
各種パッケージによる実装
- PythonのPILやOpenCVでは後者の動作となる。
- TensorFlowやPyTorchのリサイズ系関数ではalign_cornersというオプションで指定できる。
最近傍法
最近傍法(nearest)では連続化された座標から最も近い画素の色をそのままコピーすることで補間を行う。
最もシンプルな拡大アルゴリズムであり処理が早いが、拡大後の画像には不自然さが残る。
ある画素から隣の画素までの領域の半分を自分と同じ色で埋めることになるので、補間フィルターの形は以下のようになる。
\begin{align} k(s) := \begin{cases} 1 &(-1/2 \leq s <1/2) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \end{align}
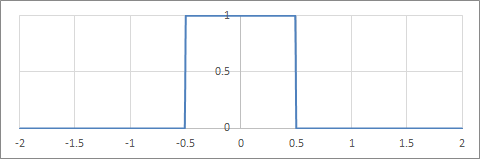
最近傍法の補間フィルター
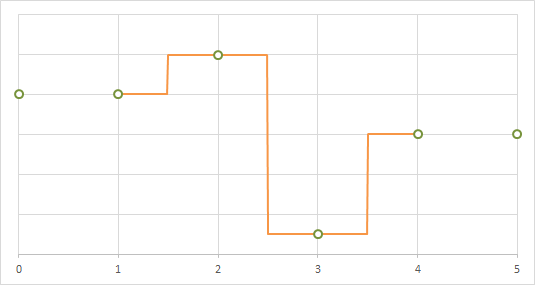
1次元に適用した場合の補間の例
(緑は補間前の離散の値で、橙はそれを連続に補間した値)
線形補間
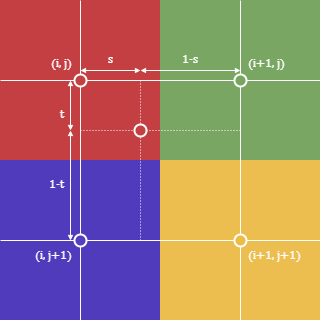
線形補間(bilinear)では、距離に応じた割合で隣接する画素の値を混ぜ合わせることで補間色が決定される。
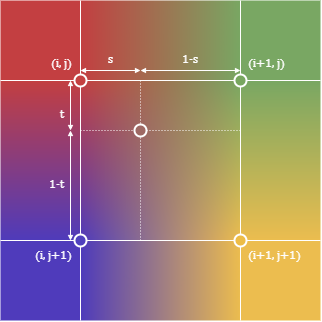
上図の場合、補間色は以下の式により求められる。
\begin{align} \tilde{p}(i+s, j+t) = (1-t)((1-s)p_{i,j} + sp_{i+1,j}) + t((1-s)p_{i,j+1} + sp_{i+1,j+1}) \end{align}
補間色はそれぞれの変数について1次式によって表現されるので、補間フィルターも1次式(の組み合わせ)となる。
\begin{align} k(s) := \begin{cases} 1-|s| &(|s| < 1) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \end{align}
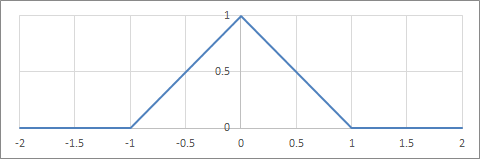
線形補間の補間フィルター
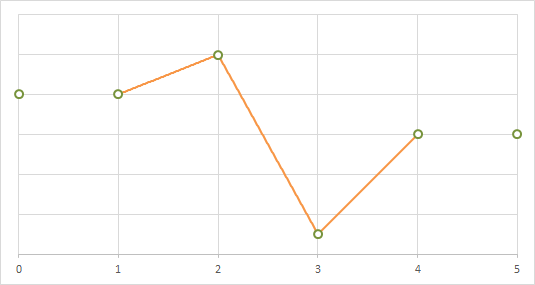
1次元に適用した場合の補間の例
3次スプライン補間
3次スプライン補間(Cubic Spline Interpolation)は3次式によって構成される補間フィルターで実行される補間。
多くの画像処理ソフトやライブラリにおいて「Bicubic」の名称が当てられている。
一般系
3次スプラインフィルターの一般系は以下の式で表される。
\begin{align} k(s) := \begin{cases} P|s|^3+Q|s|^2+R|s|+S &(|s| < 1) \\ T|s|^3+U|s|^2+V|s|+W &(1 \leq |s| < 2) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \end{align}
この式に2つの条件を与えることで、パラメーター\((P, Q, R, S, T, U, V, W)\)に制約を加える。
- 関数は各区間の端で滑らかに接続する。
- 色が一定の画像は補間した値も同じ色になる。
条件1は\(s=0,1,2\)それぞれにおいて、\(k\)と\(k'\)が共に連続になっていることを意味する。つまり、以下の5つの式が成り立つことと同値。
\begin{align} R &= 0 \tag{2} \\ P+Q+R+S &= T+U+V+W \tag{3} \\ 3P+2Q+R &= 3T+2U+V \tag{4} \\ 8T+4U+2V+W &= 0 \tag{5} \\ 12T+4U+V &= 0 \tag{6} \\ \end{align}
条件2は記事冒頭で述べた通り、\(\forall s\in [0,1]\)に対して式(1)が成り立つことを意味する。
\begin{align} 1 =& \sum_{i=-\infty}^{\infty} k(s-i) \\ =& k(s-2) + k(s-1) + k(s) + k(s+1) \\ =& P(1-s)^3 + Q(1-s)^2 + R(1-s) + S + Ps^3 + Qs^2 + Rs + S \\ & + T(2-s)^3 + U(2-s)^2 + V(2-s) + W + T(1+s)^3 + U(1+s)^2 + V(1+s) + W \\ =& P(3s^2-3s+1) + Q(2s^2-2s+1) + R + 2S \\ & + T(9s^2-9s+9) + U(2s^2-2s+5) + 3V + 2W \\ =& (3P+2Q+9T+2U)(s^2-s) + P+Q+R+2S+9T+5U+3V+2W \tag{7} \\ \end{align}
\((s^2-s)\)の係数は式(2), (4), (6)を用いて次のように変形できる。
\begin{align} 3P+2Q+9T+2U &= 3P+2Q+0+9T+2U \\ &= 3P+2Q+R+9T+2U \tag{式(2)より} \\ &= 3T+2U+V+9T+2U \tag{式(4)より} \\ &= 12T+4U+V \\ &= 0 \tag{式(6)より} \end{align}
よって式(7)は最終的に次のようになる。
\begin{align} 1 = P+Q+R+2S+9T+5U+3V+2W \tag{8} \end{align}
(2), (3), (4), (5), (6), (8)の6つの条件により、8つのパラメーターは2つにまで減らすことができる。
\begin{align} \begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & -1 & -1 & -1 \\ 3 & 2 & 1 & -3 & -2 & -1 \\ 0 & 0 & 0 & 8 & 4 & 2 \\ 0 & 0 & 0 & 12 & 4 & 1 \\ 1 & 1 & 1 & 9 & 5 & 3 \\ \end{pmatrix} \begin{pmatrix} P \\ Q \\ R \\ T \\ U \\ V \\ \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \\ -2 & -2 & 1 \\ \end{pmatrix} \begin{pmatrix} S \\ W \\ 1 \\ \end{pmatrix} \\ \Rightarrow \begin{pmatrix} P \\ Q \\ R \\ T \\ U \\ V \\ \end{pmatrix} = \frac{1}{4} \begin{pmatrix} 14 & -1 & -6 \\ -20 & 1 & 8 \\ 0 & 0 & 0 \\ -2 & -1 & 2 \\ 8 & 5 & -8 \\ -8 & -8 & 8 \\ \end{pmatrix} \begin{pmatrix} S \\ W \\ 1 \\ \end{pmatrix} \\ \end{align}
よって、3次スプラインのフィルターは変数\((S, W)\)を用いて次のように表すことができる。
\begin{align} k(s) := \frac{1}{4} \begin{cases} (14S-W-6)|s|^3 &+(-20S+W+8)|s|^2 &&+4S &(|s| < 1) \\ (-2S-W+2)|s|^3 &+(8S+5W-8)|s|^2 &+(-8S-8W+8)|s| &+4W &(1 \leq |s| < 2) \\ 0 &&& &(\mathrm{otherwise}) \\ \end{cases} \end{align}
Cardinal Spline
Hermite Spline
Cardinal Splineの説明の前に、前提としてHermite Splineについて説明する。
Hermite Splineは一般にベクトル空間上の点の集合を補間して曲線を形成するアルゴリズム。
2つの点\(p_0, p_1\)と2つのベクトル\(m_0, m_1\)が与えられているとする。
\(p_0, p_1\)を通るように連続な曲線で補間し、その曲線の\(p_0, p_1\)におけるそれぞれの接線が\(m_0, m_1\)と一致するようにしたい。
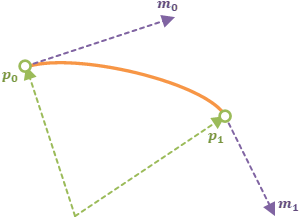
Hermite Splineの例
ベクトルパラメーター\(a, b, c, d\)を用いて補間を
\begin{align} p(s) = s^3a + s^2b + sc + d \end{align}
と表すと、
\begin{align} p_0 &= p(0) = d \\ p_1 &= p(1) = a+b+c+d \\ m_0 &= p'(0) = c \\ m_1 &= p'(1) = 3a+2b+c \\ \end{align}
となる。
これを逆に解くと各パラメーターは次のように表される。
\begin{array}{llllllll} a &= 2p_0 &-&2p_1 &+&m_0 &+&m_1 \\ b &= -3p_0 &+&3p_1 & -&2m_0 &-&m_1 \\ c &= &&&&m_0 \\ d &= p_0 \\ \end{array}
したがって補間関数は最終的に以下の形になる。
\begin{align} p(s) = (2s^3-3s^2+1)p_0 + (-2s^3+3s^2)p_1 + (s^3-2s^2+s)m_0 + (s^3-s^2)m_1 \end{align}
画像に適用する場合は\(m_i\)は与えられないので、\(m_i\)を\(p_i\)から作り出す必要がある。具体的には次のCardinal Splineで説明する。
Cardinal Spline
Cardinal Splineではパラメーター\(C\in [0,1]\)を用いて\(m_i\)を次のように定義する。
\begin{align} m_i = C\frac{p_{i+1}-p_{i-1}}{s_{i+1}-s_{i-1}} \end{align}
画像の補間においては\(s_{i} := i/2\)とする。
これにより補間関数は以下のように表すことができる。
\begin{array}{lll} p(s) &=& (2s^3-3s^2+1)p_0 + (-2s^3+3s^2)p_1 + (s^3-2s^2+s)m_0 + (s^3+s^2)m_1 \\ &=& (2s^3-3s^2+1)p_0 + (-2s^3+3s^2)p_1 + (s^3-2s^2+s)C(p_1-p_{-1}) + (s^3+s^2)C(p_2-p_0) \\ &=& -C(s^3-2s^2+s)p_{-1} \\ && + ((-C+2)s^3+(C-3)s^2+1)p_0 \\ && + ((C-2)s^3+(-2C+3)s^2+Cs)p_1 \\ && + C(s^3-s^2)p_2 \end{array}
これを補間フィルターの形式に変形する。
\(|s|<1\)のときは、\(p_0\)の係数がそのまま補間フィルターとなる。
\begin{align} k(s) = (-C+2)|s|^3+(C-3)|s|^2+1 \end{align}
\(1\leq |s|<2\)のときは、\(p_{-1}\)の係数の変数を変換したものが補間フィルターとなる。
\begin{align} k(s) &= -C\left( (|s|-1)^3 - 2(|s|-1)^2 + (|s|-1)^3 \right) \\ &= -C\left( |s|^3-5|s|^2+8|s|-4 \right) \end{align}
まとめると、Cardinal Splineは以下のようになる。
\begin{align} k(s) := \begin{cases} (-C+2)s^3+(C-3)s^2+1 &(|s| < 1) \\ -C\left( |s|^3-5|s|^2+8|s|-4 \right) &(1 \leq |s| < 2) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \end{align}
Cardinal Splineは3次スプラインの内、\(k(0)=1\)となる制約を追加で課したスプラインの集合となっている。
\(k(0)=1\)であるので、Cardinal Splineで補間した結果は必ず元の離散値を通過する。逆に言えば、\(k(0)=1\)の制約を満たさない3次スプラインでは補間結果は元の離散値を通らず、特に\(k(0)<1\)の場合はぼかしがかかったような見た目になる。
C=0の場合
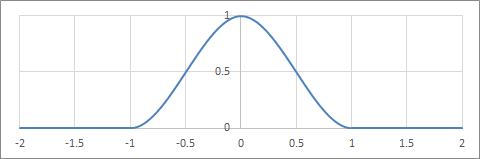
Cardinas Spline (C=0)の補間フィルター
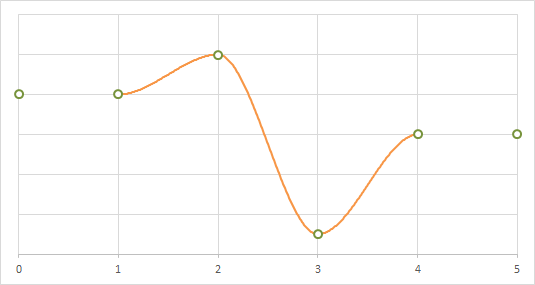
1次元に適用した場合の補間の例
C=0.5の場合
Catmull-Rom Splineとも言う。
PythonモジュールのPIL(Image.BICUBIC)などはこのパラメーターで実装されている
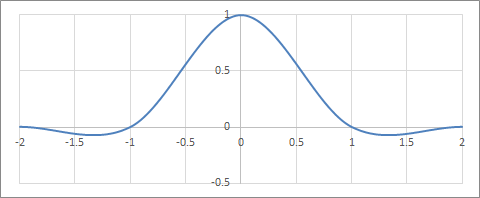
Cardinas Spline (C=0.5)の補間フィルター
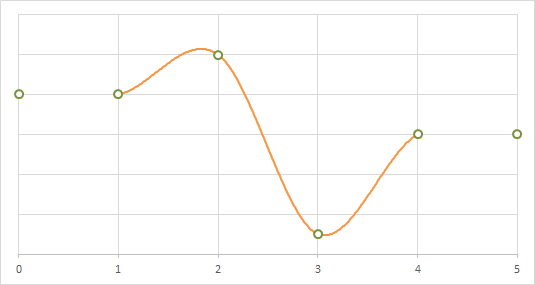
1次元に適用した場合の補間の例
図の2番目の点の周辺を見るとわかるように、Cardinal SplineにおいてC>0の場合、補間した値は元の離散値の範囲を超える場合がある。このような現象をリンギングと呼ぶ。
もし画像補間で補間したRGB値が0を下回ったり、255を上回ったりした場合はそれぞれ0・255に置き換える必要がある。
C=0.75の場合
PythonモジュールのOpenCV(cv2.INTER_CUBIC)・PyTorch(bicubic)、またPhotoshop(Bicubic)はこのパラメーターで実装されている。
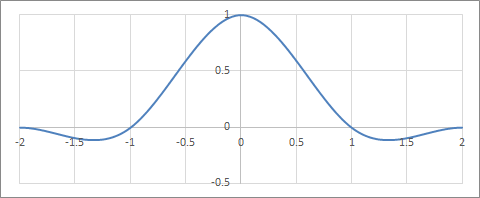
Cardinas Spline (C=0.75)の補間フィルター
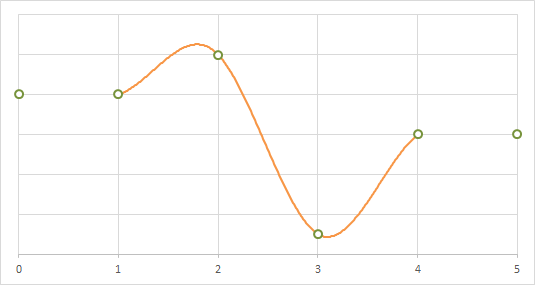
1次元に適用した場合の補間の例
B-spline
B-spline(Basis spline)もまたHermite Splineと同様に一般のベクトル空間の点の集合に対して行われる補間アルゴリズムである。
\(\{p_i\}_{i=0}^n\)を離散な点(制御点)とすると、\(\{p_i\}_{i=0}^n\)のk次B-spline補間は次の式で与えられる。
\begin{align} p(s) = \sum_{i=0}^{n} N_{i,k}(s)p_i \\ \end{align}
ここでB-spline基底関数\(N_{i,k}(s)\)は次のように逐次的に定義される関数。
\begin{align} N_{i,0}(s) &:= \begin{cases} 1 &(s_i \leq s < s_{i+1}) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \\ N_{i,k}(s) &:= \frac{s-s_i}{s_{i+k}-s_i}N_{i,k-1}(s) + \frac{s_{i+k+1}-s}{s_{i+k+1}-s_{i+1}}N_{i+1,k-1}(s) \end{align}
1次B-splineは制御点同士を線分で結ぶ線形補間であり、k次B-splineは線形補間をk回繰り返したものと解釈することができる。
このアルゴリズムは、Bézier曲線(ベジェ曲線)に使われるものと同じアルゴリズムとしても知られる。
画像に適用する場合、基底関数が補間フィルターの役割を果たすことになる。\(s_i=i\)として基底関数の具体的な形を見ていく。
k=0は最近傍法と同じ形になる。
\begin{align} N_{i,0}(s) = \begin{cases} 1 &(i \leq s < i+1) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \\ \end{align}
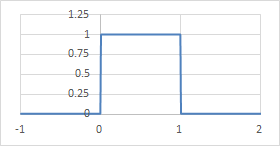
0次B-spline基底(\(N_{0,0}\))
k=1は線形補間と同じ形になる。
\begin{align} N_{i,1}(s) = \begin{cases} s-i &(i \leq s < i+1) \\ i+2-s &(i+1 \leq s < i+2) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \\ \end{align}
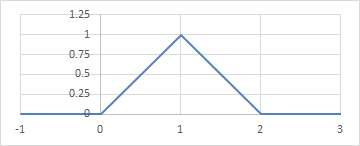
1次B-spline基底(\(N_{0,1}\))
k=2の場合。
\begin{align} N_{i,2}(s) = \begin{cases} \frac{(s-i)^2}{2} &(i \leq s < i+1) \\ -\left(s-(i+\frac{3}{2})\right)^2+\frac{3}{4} &(i+1 \leq s < i+2) \\ \frac{(i+3-s)^2}{2} &(i+2 \leq s < i+3) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \\ \end{align}
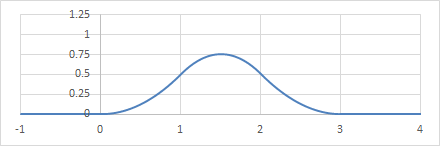
2次B-spline基底(\(N_{0,2}\))
k=3の場合。
\begin{align} N_{i,3}(s) = \begin{cases} \frac{(s-i)^3}{6} &(i \leq s < i+1) \\ -\frac{1}{2}(s-i)^3+2(s-i)^2-2(s-i)+\frac{2}{3} &(i+1 \leq s < i+2) \\ \frac{1}{2}(s-i)^3-4(s-i)^2+10(s-i)-\frac{22}{3} &(i+2 \leq s < i+3) \\ \frac{(i+4-s)^3}{6} &(i+3 \leq s < i+4) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \\ \end{align}
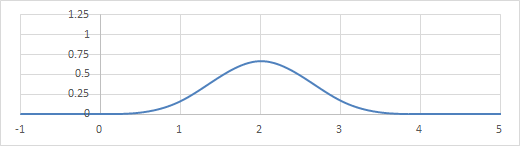
3次B-spline基底(\(N_{0,3}\))
3次B-splineを原点周辺に平行移動させると画像補間に適用できる形のフィルターを得ることができる。
\(|s|<1\)のとき、
\begin{align} k(s) &= \frac{1}{2}(|s|+2)^3-4(|s|+2)^2+10(|s|+2)-\frac{22}{3} \\ &= \frac{1}{2}|s|^3 - |s|^2 + \frac{2}{3}. \end{align}
\(1\leq |s|<2\)のとき、
\begin{align} k(s) &= \frac{(2-|s|)^3}{6} \\ &= -\frac{1}{6}|s|^3+|s|^2-2|s|+\frac{4}{3}. \end{align}
まとめると、B-splineの補間フィルターは以下のようになる。
\begin{align} k(s) := \begin{cases} \frac{1}{2}|s|^3 - |s|^2 + \frac{2}{3} &(|s| < 1) \\ -\frac{1}{6}|s|^3+|s|^2-2|s|+\frac{4}{3} &(1 \leq |s| < 2) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \end{align}
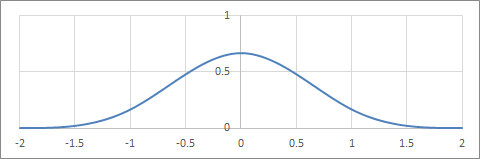
(3次)B-splineの補間フィルター
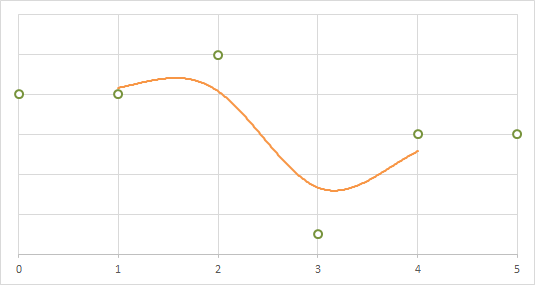
1次元に(3次)B-splineを適用した場合の補間の例
Mitchell-Netravali Filters
Mitchell-Netravali FiltersはCardinal SplineとB-splineを統合したフィルター群。
3次スプラインが2つのパラメーターによって表現されることは既に示したが、Mitchell-Netravali Filtersでは\(B, C\)というパラメータを使って3次スプラインを表現する。
具体的には、\(B=0\)のときCardinal Spline、\((B,C)=(1,0)\)のときにB-splineとなるように構成する。
Cardinal Splineのフィルターを\(k_C\)、B-splineのフィルターを\(k_B\)とすると、Mitchell-Netravali Filtersは次のように定義される。
\begin{align} k(s) := k_C(s;C) + B\left(k_B(s)-k_C(s;C)\right) \end{align}
つまり、
\begin{align} k(s) = \frac{1}{6} \begin{cases} (12-9B-6C)|s|^3 + (-18+12B+6C)|s|^2 + 6-2B &(|s| < 1) \\ (-B-6C)|s|^3 + (6B+30C)|s|^2 + (-12B-48C)|s| + 8B+24C &(1 \leq |s| < 2) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \end{align}
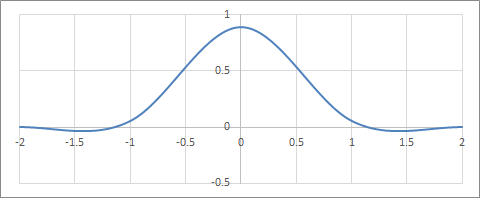
(B, C) = (1/3, 1/3)の補間フィルター
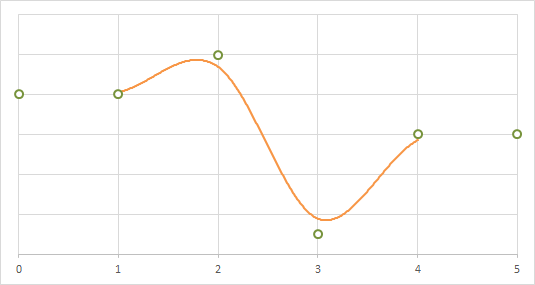
(B, C) = (1/3, 1/3)を1次元に適用した場合の補間の例
C-B平面の分類
Mitchellは更にC-B平面のそれぞれのパラメーターに対して、下図のように専門家の主観による分類を行った。Satisfactoryとなっている部分が違和感の少ない補間フィルターとなる。
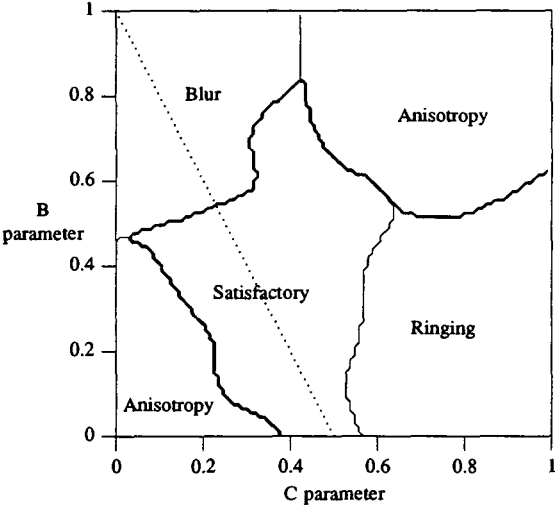
Mitchellが調査した主観に基づくC-B平面の分類
Keysによると、ある関数\(f(x)\)と、その関数を間隔\(h\)でサンプリングしてから補間した再現関数\(f_r(x)\)との差は、\(x\in[0,h]\)において次の式のようになる。(\(r(x/h)\)は多項式)
\begin{align} f_r(x) - f(x) = (B+2C-1)r\left(\frac{x}{h}\right)f'(0)h + O(h^2) \end{align}
したがって\(B+2C=1\)(上図の破線箇所)ならば\(f_r(x)-f(x) = O(h^2)\)となり、サンプリング間隔に対してより早く収束することになる。特にMitchellは\((B, C)=(1/3,1/3)\)を推奨値としている。
Keysの主張を証明する。
\(f(x)\)を間隔\(h\)でサンプリングし、Mitchell-Netravali Filtersによって再構成して\(f_r(x)\)を得る場合を考える。
このとき、\(x\in[0,h]\)に対して\(s:=\frac{x}{h}\)とすると、\(f_r(x)\)は次のようになる。
\begin{align} f_r(x) &= f(-h)k\left(\frac{x}{h}+1\right) + f(0)k\left(\frac{x}{h}\right) + f(h)k\left(\frac{x}{h}-1\right) + f(2h)k\left(\frac{x}{h}-2\right) \\ &= \sum_{n=0}^\infty\frac{f^{(n)}(0)}{n!}(-h)^nk\left(s+1\right) + f(0)k\left(s\right) + \sum_{n=0}^\infty\frac{f^{(n)}(0)}{n!}h^nk\left(s-1\right) + \sum_{n=0}^\infty\frac{f^{(n)}(0)}{n!}(2h)^nk\left(s-2\right) \\ &= \left(k(s+1) + k(s) + k(s-1) + k(s-2)\right)f(0) \\ &\qquad + \sum_{n=1}^\infty\left((-1)^nk(s+1) + k(s-1) + 2^nk(s-2)\right)\frac{f^{(n)}(0)}{n!}h^n \\ &= f(0) + \sum_{n=1}^\infty\left((-1)^nk(s+1) + k(s-1) + 2^nk(s-2)\right)\frac{f^{(n)}(0)}{n!}h^n \\ \end{align}
一方、\(x=sh\in[0,h]\)であることから、
\begin{align} f(x) &= \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n \\ &= f(0) + \sum_{n=1}^\infty \frac{f^{(n)}(0)}{n!}s^nh^n \\ \end{align}
なので、
\begin{align} f_r(x) - f(x) &= \sum_{n=1}^\infty\left((-1)^nk(s+1) + k(s-1) + 2^nk(s-2)\right)\frac{f^{(n)}(0)}{n!}h^n - \sum_{n=1}^\infty \frac{f^{(n)}(0)}{n!}s^nh^n \\ &= \sum_{n=1}^\infty\left((-1)^nk(s+1) + k(s-1) + 2^nk(s-2) - s^n\right)\frac{f^{(n)}(0)}{n!}h^n \\ \end{align}
となる。
ここで、\(g_n(s) := (-1)^nk(s+1) + k(s-1) + 2^nk(s-2)\)とすると、
\begin{align} g_n(s) =& (-1)^nk\left(s+1\right) + k\left(s-1\right) + 2^nk\left(s-2\right) \\ =& \frac{(-1)^n}{6}\left( (-B-6C)(s+1)^3 + (6B+30C)(s+1)^2 + (-12B-48C)(s+1) + 8B+24C \right) \\ & + \frac{1}{6}\left( (12-9B-6C)(1-s)^3 + (-18+12B+6C)(1-s)^2 + 6-2B \right) \\ & + \frac{2^n}{6}\left( (-B-6C)(2-s)^3 + (6B+30C)(2-s)^2 + (-12B-48C)(2-s) + 8B+24C \right) \\ =& \frac{(-1)^n}{6}\left( (-B-6C)s^3 + (3B+12C)s^2 + (-3B-6C)s + B \right) \\ & + \frac{1}{6}\left( (-12+9B+6C)s^3 + (18-15B-12C)s^2 + (3B+6C)s + B \right) \\ & + \frac{2^n}{6}\left( (B+6C)s^3 - 6Cs^2 \right) \\ =& \left(\frac{9-(-1)^n+2^n}{6}B + (1-(-1)^n+2^n)C - 2\right)s^3 \\ & + \left(\frac{-15+3\cdot(-1)^n}{6}B + (-2+2\cdot(-1)^n-2^n)C + 3\right)s^2 \\ & + \left(\frac{1-(-1)^n}{2}B + (1-(-1)^n)C\right)s \\ & + \frac{1+(-1)^n}{6}B \end{align}
と表すことができ、具体的には、
\begin{align} g_1(s) &= (2B+4C-2)s^3 + (-3B-6C+3)s^2 + (B+2C)s \\ &= (B+2C-1)(2s^3 - 3s^2 + s) + s \\ \end{align}
\begin{align} g_2(s) &= (2B+4C-2)s^3 + (-2B-4C+3)s^2 + \frac{B}{3} \\ &= 2(B+2C-1)(s^3 - s^2) + s^2 + \frac{B}{3} \\ \end{align}
\begin{align} g_3(s) &= (3B+10C-2)s^3 + (-3B-12C+3)s^2 + (B+2C)s \\ &= (B+2C-1)(5s^3 - 6s^2 + s) + (-2B+3)s^3 + 3(B-1)s^2 + s \\ \end{align}
となる。
したがって、
\begin{align} f_r(x) - f(x) &= \sum_{n=1}^\infty\left(g_n(s) - s^n\right)\frac{f^{(n)}(0)}{n!}h^n \\ &= (B+2C-1)(2s^3 - 3s^2 + s)f'(0)h \\ &\qquad + \left(2(B+2C-1)(s^3 - s^2) + \frac{B}{3}\right)\frac{f^{(2)}(0)}{2}h^2 \\ &\qquad + \left((B+2C-1)(5s^3 - 6s^2 + s) + 2(-B+1)s^3 + 3(B-1)s^2 + s\right)\frac{f^{(3)}(0)}{6}h^3 \\ &\qquad + O(h^4) \\ &= (B+2C-1)(2s^3 - 3s^2 + s)f'(0)h + O(h^2) \\ \end{align}
という評価が得られ、\(r(s):=2s^3-3s^2+s\)とすればKeysの主張が成り立つ。
ここで、\(B+2C=1\)という条件の下では、具体的には
\begin{align} f_r(x) - f(x) &= \frac{B}{3}\frac{f^{(2)}(0)}{2}h^2 + \left(2(-B+1)s^3 + 3(B-1)s^2 + s\right)\frac{f^{(3)}(0)}{6}h^3 + O(h^4) \end{align}
という評価が成り立つ。
特に、\((B,C)=(0,1/2)\) (=Catmull-Rom Spline) としたとき、
\begin{align} f_r(x) - f(x) &= \left(2s^3 - 3s^2 + s\right)\frac{f^{(3)}(0)}{6}h^3 + O(h^4) \end{align}
となって、より高い補間精度が成り立つことがわかる。
なお、\(2s^3-3s^2+s = s(s-1)(2s-1)\)なので、\(s=0, \frac{1}{2}, 1\)となる点では\(B, C\)の値によらず\(O(h^2)\)の補間精度を達成することになる。
これは例えばalign_corners=Trueで\(N\times M→(2N-1)\times(2M-1)\)と拡大する場合が該当し、このとき拡大後の全てのピクセルは全て\(s=0, \frac{1}{2}, 1\)のいずれかとなる。
C-B平面上のフィルターの変化の例を以下にアニメーションで示す。
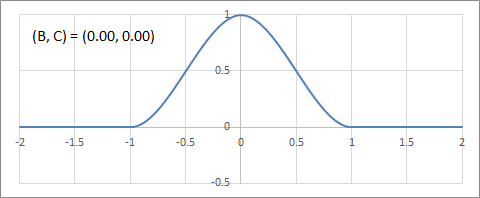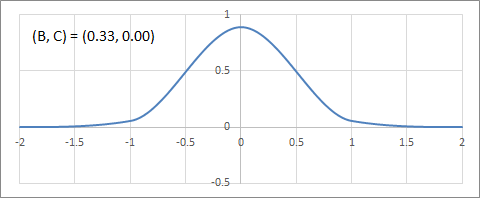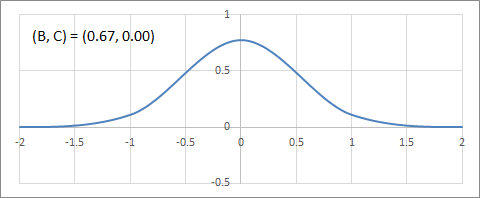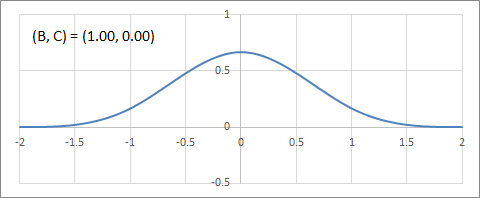
B軸(Duff's tensioned B-splines)上の補間フィルターの変化
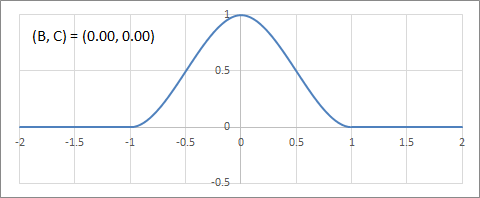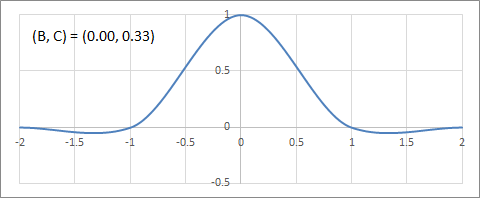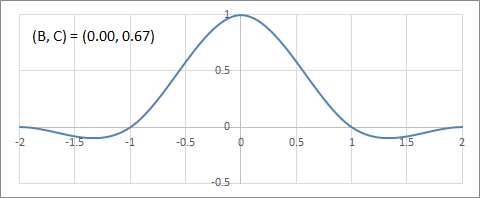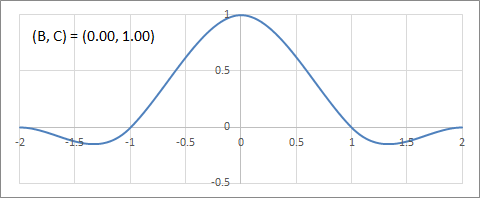
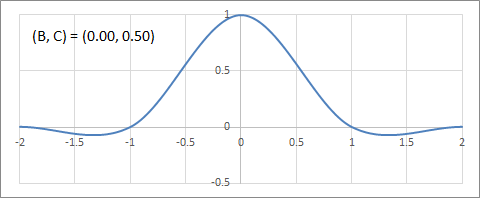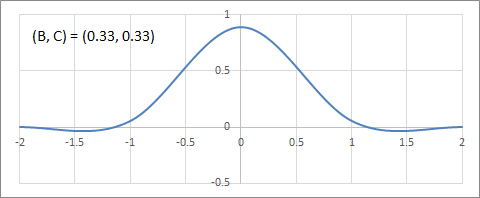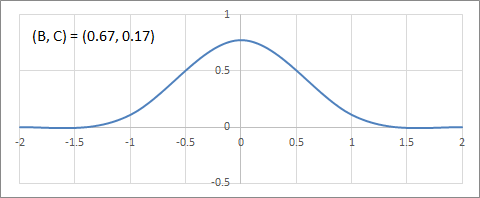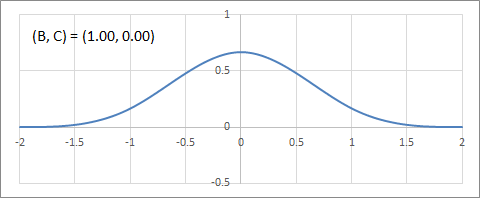
C軸(Cardinal Splines)上の補間フィルターの変化
B+2C=1上の補間フィルターの変化
各パッケージ・アプリの対応
似たような名称でも実装がそれぞれ異なるので注意が必要。
- Paint.NETは「Use gamma correction」のチェックを外して拡大した場合を調べた
- GIMPもLinear RGB空間で補間が行われるので、出力後に別途ガンマ補正を外して調べた
| B, C | 名称 | パッケージ・アプリ | オプション |
|---|---|---|---|
| 0, 0 | (Cardinal Splineの一種) | ImageMagick | -filter Hermite |
| 0, 0.5 | Catmull-Rom Spline | Paint.NET | Bicubic |
| Affinity | Bicubic | ||
| ImageMagick | -filter Catrom | ||
| Excel | (画像やグラフの補間に自動で使われる) | ||
| PIL | resample=Image.BICUBIC | ||
| TensorFlow | method=tensorflow.ResizeMethod.BICUBIC | ||
| 0, 0.75 | (Cardinal Splineの一種) | Photoshop | Bicubic |
| OpenCV | interpolation=cv2.INTER_CUBIC | ||
| PyTorch | mode='bicubic' | ||
| 1/3, 1/3 | - | ImageMagick | -filter Mitchell |
| 0.5, 0.25 | - | GIMP | Cubic |
| 1, 0 | B-spline | Paint.NET | Bicubic (Smooth) |
| ImageMagick | -filter Cubic |
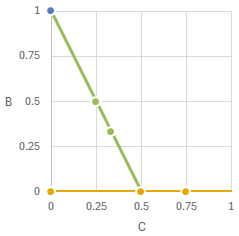
各実装のC-B平面上の位置
Lanczos補間
Lanczos補間はsinc関数によって構成されるフィルターを用いた補間。ハンガリーの数学者Cornelius Lanczosによって考案された。
画像の縮小に対して効果を発揮するとされている。
フィルターは以下のように定義される。\(n\in N\)は半径パラメーター。
\begin{align} \kappa(x) := \begin{cases} \mathrm{sinc}(\pi x)\mathrm{sinc}(\frac{\pi x}{n}) &(|x|\leq n) \\ 0 &(\mathrm{otherwise}) \\ \end{cases} \end{align}
\begin{align} k(x) := \frac{\kappa(x)}{\sum_{i=-\infty}^{\infty} \kappa(x+i)} \end{align}
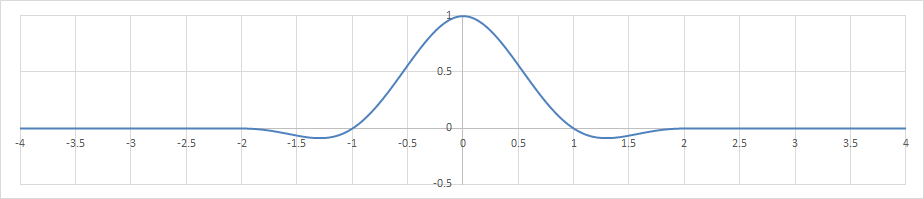
Lanczos補間(n=2)の補間フィルター
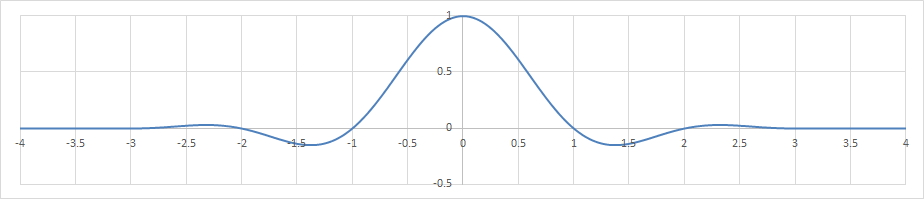
Lanczos補間(n=3)の補間フィルター
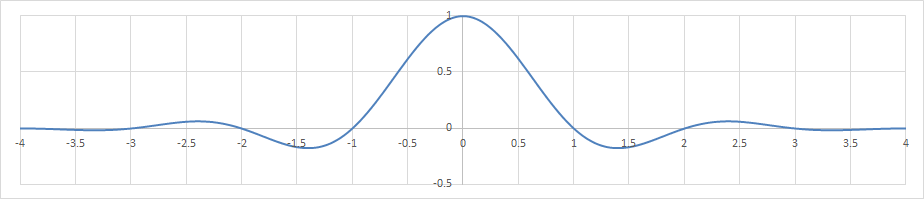
Lanczos補間(n=4)の補間フィルター
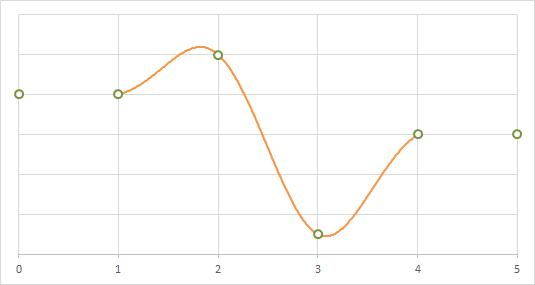
Lanczos補間(n=2)を1次元に適用した場合の補間の例
Spline16/36/64
Spline16/36/64は、Panorama Toolsの作者Helmut Derschによって考案された補間アルゴリズム。
区間\([-n+1, n]\)を\(2n-1\)等分し、それぞれの区間上で3次関数となるように補間する。(補間値そのものがSplineになっている)
係数を求めるため、3次関数\(f\)には以下の制約を与える。
- \(s=-n+1, ... , n\)において、\(f\)は離散な点\(p_{-n+1}, p_{-n+2}, ... , p_{n-1}, p_n\)を通過する。
- \(s=-n+2, ... , n-1\)において、\(f', f''\)は連続。
- \(f'(-n+1)=f'(n)=0.\)
具体的な導出過程は省略するが、例えばSpline16(n=2)の補間フィルターは以下のように表される。\(n\)はフィルターの半径であり、Spline36、Spline64と増えていくと3次式の数も3つ4つと増えていく。
なお、補間の過程で現れる関数自体は滑らかになるが、補間フィルターは各区間の端で微分可能にはならない。(連続にはなる)
\begin{align} k(s) := \begin{cases} |s|^3 &-\frac{9}{5}|s|^2 &-\frac{1}{5}|s| &+1 &(|s| < 1) \\ -\frac{1}{3}|s|^3 &+\frac{9}{5}|s|^2 &-\frac{46}{15}|s| &+\frac{8}{5} &(1 \leq |s| < 2) \\ 0 &&& &(\mathrm{otherwise}) \\ \end{cases} \end{align}
平均画素法
平均画素法(area average)はここまでの補間アルゴリズムのように連続画像から等間隔に点を取るのではなく、等間隔に区切られた領域内の最近傍法による連続値の平均を新たな画素の値とする方法。
平均画素法は画像縮小によく使われる。連続に補間して等間隔に新たな点を取る方法では元画像の細い線の情報を取りこぼす可能性があるが、平均画素法を用いると元画像の全ての画素がリサイズ結果に影響を与えることが保証される。
カーネルは定義不可能。

3x3を2x2に縮小する例
実行例
4倍に拡大する例
例1

リサイズ対象画像

最近傍法

線形補間

Cubic Spline (B, C) = (0, 0)

Cubic Spline (B, C) = (0, 0.5) (Catmull-Rom Spline)

Cubic Spline (B, C) = (0, 0.75)

Cubic Spline (B, C) = (0, 1)

Cubic Spline (B, C) = (1/3, 1/3)

Cubic Spline (B, C) = (1, 0) (B-Spline)

Cubic Spline (B, C) = (1, 1)

Lanczos n=2

Lanczos n=3

Lanczos n=4
例2

リサイズ対象画像

最近傍法

線形補間

Cubic Spline (B, C) = (0, 0)

Cubic Spline (B, C) = (0, 0.5) (Catmull-Rom Spline)

Cubic Spline (B, C) = (0, 0.75)

Cubic Spline (B, C) = (0, 1)

Cubic Spline (B, C) = (1/3, 1/3)

Cubic Spline (B, C) = (1, 0) (B-Spline)

Cubic Spline (B, C) = (1, 1)

Lanczos n=2

Lanczos n=3

Lanczos n=4
ソースコード
これらの画像を作るために使ったPythonのソースコード。
並列化していないので非常に遅い。
from abc import ABCMeta, abstractmethod
import numpy as np
import cv2
import matplotlib.pyplot as plt
class Filter(metaclass=ABCMeta):
def __init__(self, radius):
self.__radius = radius
@abstractmethod
def __call__(self, x):
pass
def radius(self):
return self.__radius
class NearestFilter(Filter):
def __init__(self):
super().__init__(1)
def __call__(self, x):
x = abs(x)
if x < 1/2:
return 1
else:
return 0
class LinearFilter(Filter):
def __init__(self):
super().__init__(1)
def __call__(self, x):
x = abs(x)
if x < 1:
return 1 - x
else:
return 0
class MitchellNetravaliFilter(Filter):
def __init__(self, b=1/3, c=1/3):
super().__init__(2)
self.b = b
self.c = c
def __call__(self, x):
x = abs(x)
if x < 1:
return ((12-9*self.b-6*self.c)*x**3 + (-18+12*self.b+6*self.c)*x**2 + 6-2*self.b)/6
elif x < 2:
return ((-self.b-6*self.c)*x**3 + (6*self.b+30*self.c)*x**2 + (-12*self.b-48*self.c)*x + 8*self.b+24*self.c)/6
else:
return 0
class LanczosFilter(Filter):
def __init__(self, radius=2):
super().__init__(radius)
self.weight_cache = {}
def __call__(self, x):
x = abs(x)
if x < self.radius():
z = x % 1
if z in self.weight_cache:
w = self.weight_cache[z]
else:
w = sum([self.f(i+z) for i in range(-self.radius(), self.radius())])
self.weight_cache[z] = w
return self.f(x) / w
else:
return 0
def f(self, x):
return np.sinc(x)*np.sinc(x/self.radius())
def visualize_kernel(kernel, num=100):
x = np.linspace(-kernel.radius()-1, kernel.radius()+1, int(2*num*(kernel.radius()+1))+1)
y = np.frompyfunc(kernel, 1, 1)(x)
plt.plot(x, y)
plt.show()
def interpolate_1d(image, k_max, kernel):
i_max = image.shape[0]
new_image = np.zeros(k_max)
for k in range(k_max):
s = i_max/k_max*(k+1/2)-1/2
i = int(np.floor(s))
s = s - i
v = 0
for n in range(-kernel.radius()+1, kernel.radius()+1): # -r+1, -r+2, ..., 0, ... , r-1, r
i2 = i + n
if i2 < 0:
i2 = 0
elif i2 >= i_max:
i2 = i_max - 1
v += image[i2]*kernel(-n+s)
new_image[k] = v
return new_image
def interpolate_2d(image, scale_factor, kernel):
# IxJ -> KxL
j_max, i_max, _ = image.shape
l_max = j_max*scale_factor
k_max = i_max*scale_factor
# 横方向
new_image = np.zeros((j_max, k_max, 3))
for j in range(j_max):
for c in range(3):
new_image[j, :, c] = interpolate_1d(image[j, :, c], k_max, kernel)
# 縦方向
new_image_2 = np.zeros((l_max, k_max, 3))
for k in range(k_max):
for c in range(3):
new_image_2[:, k, c] = interpolate_1d(new_image[:, k, c], l_max, kernel)
return new_image_2
if __name__ == '__main__':
# # visualize kernel
# visualize_kernel(NearestFilter())
# visualize_kernel(LinearFilter())
# visualize_kernel(MitchellNetravaliFilter(1, 0))
# visualize_kernel(LanczosFilter(4))
# resize
image = cv2.imread('../image/2d-example/2d-example-1.png')
cv2.imwrite('save/2d-example-1-nearest.png', interpolate_2d(image, 4, NearestFilter()))
cv2.imwrite('save/2d-example-1-linear.png', interpolate_2d(image, 4, LinearFilter()))
cv2.imwrite('save/2d-example-1-cubic-0-0.png', interpolate_2d(image, 4, MitchellNetravaliFilter(0, 0)))
cv2.imwrite('save/2d-example-1-catmull-rom.png', interpolate_2d(image, 4, MitchellNetravaliFilter(0, 0.5)))
cv2.imwrite('save/2d-example-1-cubic-0-0.75.png', interpolate_2d(image, 4, MitchellNetravaliFilter(0, 0.75)))
cv2.imwrite('save/2d-example-1-cubic-0-1.png', interpolate_2d(image, 4, MitchellNetravaliFilter(0, 1)))
cv2.imwrite('save/2d-example-1-mitchell-netravali.png', interpolate_2d(image, 4, MitchellNetravaliFilter(1/3, 1/3)))
cv2.imwrite('save/2d-example-1-b-spline.png', interpolate_2d(image, 4, MitchellNetravaliFilter(1, 0)))
cv2.imwrite('save/2d-example-1-cubic-1-1.png', interpolate_2d(image, 4, MitchellNetravaliFilter(1, 1)))
cv2.imwrite('save/2d-example-1-lanczos-2.png', interpolate_2d(image, 4, LanczosFilter(2)))
cv2.imwrite('save/2d-example-1-lanczos-3.png', interpolate_2d(image, 4, LanczosFilter(3)))
cv2.imwrite('save/2d-example-1-lanczos-4.png', interpolate_2d(image, 4, LanczosFilter(4)))
pass
参考
- PixInsight Reference Documentation | Interpolation Algorithms in PixInsight
- Resampling - Avisynth wiki
- 画像リサイズのうんちく (補間フィルタ) - Qiita
- Splineリサイズの係数式とその導出法