色彩工学 (3) - RGB色空間
関連記事
- 色彩工学 (1) - CIE 1931色空間
- 色彩工学 (2) - 均等色空間
- 色彩工学 (3) - RGB色空間 (本記事)
目次
RGB色空間
一般の場合
色空間上で3次元の値として表される色を現実で利用するためには、光やインクの混ぜ合わせによって任意の色座標の色を再現するための法則を調べる必要がある。
モニターで色を再現する場合、赤・緑・青の3つの光を用いるのが自然だが、これら3つの色は等色実験で用いた原刺激\([I_R], [I_G], [I_B]\)と必ずしも容易に一致させることができるとは限らない。
モニターの発光素子の三原色と参照白色光のxy色度座標が次のように与えられているとする。
(三刺激値が\((1,1,1)\)の光は参照白色光と等色となる必要がある。)
\begin{align} \begin{cases} w &= (w_x, w_y) \\ r &= (r_x, r_y) \\ g &= (g_x, g_y) \\ b &= (b_x, b_y) \\ \end{cases} \end{align}
このとき、これらの三原色で表されるモニターの色座標\((R,G,B)\)とXYZ座標との変換行列\(M\)を求めたい。
\((R,G,B)=(1,0,0)\)のとき、\((X,Y,Z)=M(R,G,B)=(M_{11},M_{21},M_{31})\)となる。このときxy色度座標は\((r_x, r_y)\)とならなければならないので、
\begin{align} \begin{cases} r_x = \frac{M_{11}}{M_{11}+M_{21}+M_{31}} \\ r_y = \frac{M_{21}}{M_{11}+M_{21}+M_{31}} \\ \end{cases} \end{align}
となる。\(\alpha_r := M_{11}+M_{21}+M_{31}\)とすれば、
\begin{align} \begin{cases} M_{11} = \alpha_r r_x \\ M_{21} = \alpha_r r_y \\ M_{31} = \alpha_r (1 - r_x - r_y) \\ \end{cases} \end{align}
\(G, B\)についても同様なので、\(M\)は次のようになる。
\begin{align} M = \begin{pmatrix} \alpha_r r_x & \alpha_g g_x & \alpha_b b_x \\ \alpha_r r_y & \alpha_g g_y & \alpha_b b_y \\ \alpha_r (1 - r_x - r_y) & \alpha_g (1 - g_x - g_y) & \alpha_b (1 - b_x - b_y) \\ \end{pmatrix} \end{align}
\((R,G,B)=(1,1,1)\)は参照白色光と等色とならなければならない。参照白色光の光度を\(Y_w\)とすると、
\begin{align} \frac{Y_w}{w_y} \begin{pmatrix} w_x \\ w_y \\ 1-w_x-w_y \\ \end{pmatrix} &= M \begin{pmatrix} 1 \\ 1 \\ 1 \\ \end{pmatrix}\\ &= \begin{pmatrix} \alpha_r r_x + \alpha_g g_x + \alpha_b b_x \\ \alpha_r r_y + \alpha_g g_y + \alpha_b b_y \\ \alpha_r (1 - r_x - r_y) + \alpha_g (1 - g_x - g_y) + \alpha_b (1 - b_x - b_y) \\ \end{pmatrix} \\ &= \begin{pmatrix} r_x & g_x & b_x \\ r_y & g_y & b_y \\ 1 - r_x - r_y & 1 - g_x - g_y & 1 - b_x - b_y \\ \end{pmatrix} \begin{pmatrix} \alpha_r \\ \alpha_g \\ \alpha_b \\ \end{pmatrix} \\ \end{align}
したがって未知の係数\(\alpha_r, \alpha_g, \alpha_b\)は次のように求めることができ、RGBとXYZの相互変換が得られる。
\begin{align} \begin{pmatrix} \alpha_r \\ \alpha_g \\ \alpha_b \\ \end{pmatrix} &= \frac{Y_w}{w_y} \begin{pmatrix} r_x & g_x & b_x \\ r_y & g_y & b_y \\ 1 - r_x - r_y & 1 - g_x - g_y & 1 - b_x - b_y \\ \end{pmatrix}^{-1} \begin{pmatrix} w_x \\ w_y \\ 1-w_x-w_y \\ \end{pmatrix} \\ \end{align}
sRGB色空間
sRGB(standard RGB)は1996年にHewlett-PackardとMicrosoftが定義し、その後1999年に国際電気標準会議(IEC)によって標準化された色空間。Webの標準の色空間として定められており、現在コンピューター上で扱うほとんど全ての画像はsRGBに基づいた値で表現されている。
蛍光体を用いたCRT(=ブラウン管)に出力して色を再現することを想定した規格。
三原色と白色点は、1993年にテレビ放送のために定められた規格Rec. 709と同じものを採用している。
(Rec. 709もまた、1968年に定義されたSMPTE Cと、1970年に定義されたPALという規格に基づいて定められている。)
\begin{align} \begin{cases} w &= (0.3127, 0.3290) \\ r &= (0.64, 0.33) \\ g &= (0.30, 0.60) \\ b &= (0.15, 0.06) \\ \end{cases} \end{align}
これらの三原色・白色点から、変換行列は次のように計算される。(\(Y_w=1\)の場合)
\begin{align} \begin{pmatrix} X \\ Y \\ Z \\ \end{pmatrix} = \begin{pmatrix} 0.4124 & 0.3576 & 0.1805 \\ 0.2126 & 0.7152 & 0.0722 \\ 0.0193 & 0.1192 & 0.9505 \\ \end{pmatrix} \begin{pmatrix} sR \\ sG \\ sB \\ \end{pmatrix} \end{align}
白色点は\(D_{65}\)であり、その輝度は本来は\(Y_w = 80 cd/m^2\)となるよう定められている。
色度が上記の\(r, g, b\)となるように発光素子を用意して、素子にかける電圧を調整することで望んだ色を表現することができることになる。
sRGBが表現可能な色は、xy色度図上で次の範囲となる。
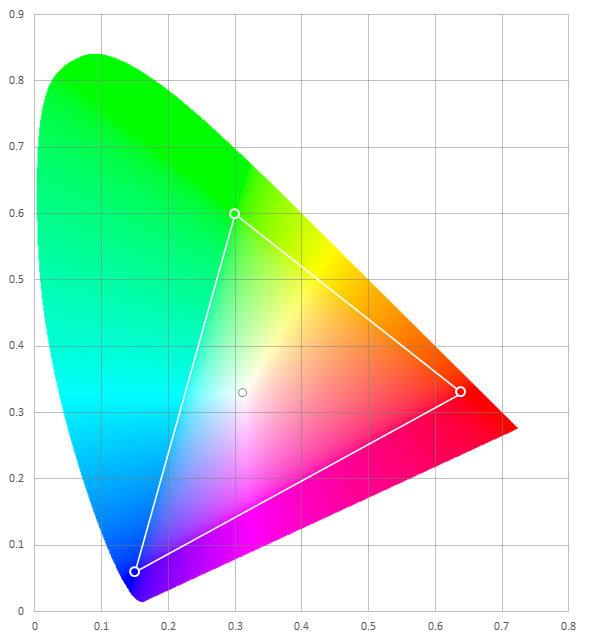
sRGBが表現可能なxy色度図上の色の範囲と白色点の座標
ガンマ補正
sRGBではXYZ座標を上述の行列によって線形変換した結果の\((sR,sG,sB)=M^{-1}(X,Y,Z)\)から、更にもう一回の変換を経て最終的なsRGBの値\((sR',sG',sB')\)を得る。
画像処理の分野でガンマという言葉は「白と黒の中間の色の明るさ」を意味する。ディスプレイの発光素子には、加えた電圧と素子が放つ光の強度が正比例しないガンマ特性という性質がある。行列変換によって直接得られた\((sR,sG,sB)\)は3つの原刺激の放射強度を表す値だが、sRGBではそれらの値をガンマ特性に従って電圧の大きさに補正して保存する仕様となっている。この補正をgamma compression(encoding gamma)と呼ぶ。
逆に、sRGBで保存されたデータをディスプレイに出力するには、ガンマ圧縮の逆の処理を行う必要がある。この処理をgamma expansion(decoding gamma)と呼ぶ。
ガンマ補正という言葉は前者を指すことが多いが、後者を含めてガンマ補正と呼ぶこともあるので注意が必要である。
ガンマ特性は、入力電圧を\(V\)、出力輝度を\(L\)とすると\(L=V^\gamma\)の関係になることがわかっている。
sRGBでは、XYZ座標から線形変換された直接の結果\((sR,sG,sB)\)の各成分\(L\)を、次の関係に従いエンコードすることでsRGB値\(V\)とする。
\begin{align} L = \begin{cases} (\frac{V+a}{1+a})^\gamma &\qquad (V \geq K_0) \\ \frac{V}{\phi} &\qquad (V < K_0) \end{cases} \end{align}
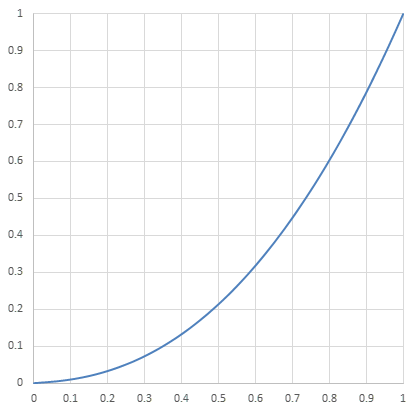
decoding gamma (V→L)
ここで、\(\gamma = 2.4\)。また、\(a = 0.055\)は暗電流の影響を反映するために定義された値とされる。関数全体は\(L=V^{2.2}\)に近い形になっている。
原点を通る直線\(\frac{V}{\phi}\)が曲線部\((\frac{V+a}{1+a})^\gamma\)と接するように\(\phi = \frac{1+a}{\gamma}\left(\frac{(1+a)(\gamma-1)}{a\gamma}\right)^{\gamma - 1} = 12.92\)が定められる。しかし、この値は小数点以下第3位以下を切り捨てているので、実際は曲線部と2点で交わる。その内\(V\)が大きい方を\(K_0 = 0.04045\)としている。また、\(K_0\)の小数点以下第5位までの値を使うと、\(V=K_0\)のとき\(L=0.0031308\)となる。
このように原点付近に直線部分を持つような定義となっている理由は計算上の都合と言われている。
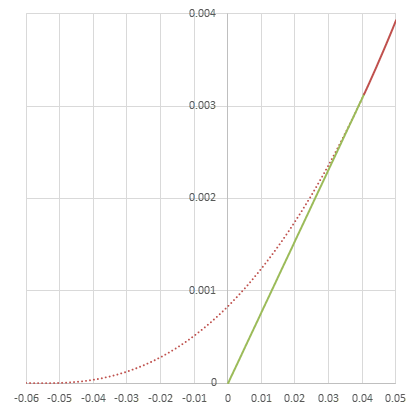
decoding gammaの原点付近の様子
sRGBはXYZからの線形変換をガンマ圧縮し、\([0, 1]\)から255倍して\(\{0, ... , 255\}\)の範囲に整数化した値が最終的なデータの値となる。
なお、ガンマ補正する前のRGBの値をガンマ補正後のR'G'B'と区別してLinear RGBと呼ぶことがある。
Adobe RGB (1998)色空間
1998年にAdobeが定義したAdobe RGBでは次の三原色・白色点を用いる。
\begin{align} \begin{cases} w &= (0.3127, 0.3290) \\ r &= (0.64, 0.33) \\ g &= (0.21, 0.71) \\ b &= (0.15, 0.06) \\ \end{cases} \end{align}
これらの三原色・白色点から、変換行列は次のように計算される。
\begin{align} \begin{pmatrix} X \\ Y \\ Z \\ \end{pmatrix} = \begin{pmatrix} 0.5767 & 0.1856 & 0.1882 \\ 0.2974 & 0.6273 & 0.0753 \\ 0.0270 & 0.0707 & 0.9911 \\ \end{pmatrix} \begin{pmatrix} sR \\ sG \\ sB \\ \end{pmatrix} \end{align}
sRGBと比べるとgのみ定義が異なる。Adobe RGBのgはNTSC(1953)に由来する値であり、sRGBよりも緑側に色域が広くなる。
Adobe RGBはsRGBに比べて色域が広いので、Adobe RGBで保存されたファイルをsRGB形式だと思い込んで開くと、(特に緑成分の)色がくすんで見えることになる。
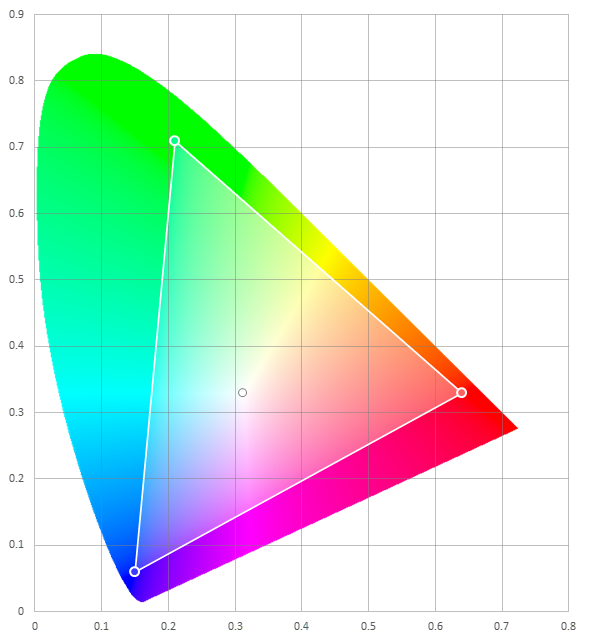
Adobe RGBが表現可能なxy色度図上の色の範囲と白色点の座標
ガンマ補正は次のように定義される。ガンマ値は\(\gamma=\frac{563}{256} \simeq 2.2\)。
sRGBとは異なり、原点付近の直線部分が存在しない簡素な形。
\begin{align} L = V^\gamma \end{align}
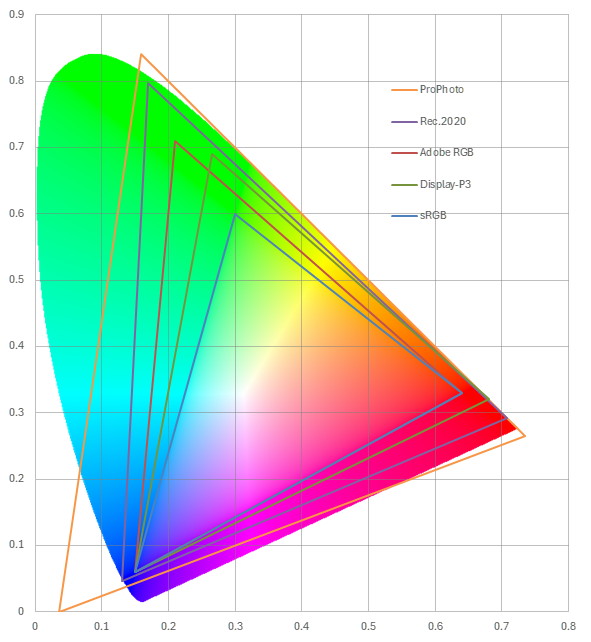
その他のRGB色空間
sRGBとAdobe RGB以外にも白色の色度座標・三原色の色度座標・ガンマを定めることで様々なRGB色空間を定義することができる。
| 名称 | 白色 | \((x_R, y_R)\) | \((x_G, y_G)\) | \((x_B, y_B)\) | \(\gamma\) |
|---|---|---|---|---|---|
| NTSC | C | (0.670, 0.330) | (0.210, 0.710) | (0.140, 0.080) | 約2.2 |
| PAL/SECAM (Rec.601) | D65 | (0.640, 0.330) | (0.290, 0.600) | (0.150, 0.060) | 約2.2 |
| SMPTE-C | D65 | (0.630, 0.340) | (0.310, 0.595) | (0.155, 0.070) | 約2.2 |
| sRGB (Rec.709) | D65 | (0.640, 0.330) | (0.300, 0.600) | (0.150, 0.060) | 約2.2 |
| Display P3 | D65 | (0.680, 0.320) | (0.265, 0.690) | (0.150, 0.060) | 約2.2 |
| Adobe RGB (1998) | D65 | (0.640, 0.330) | (0.210, 0.710) | (0.150, 0.060) | 約2.2 |
| Rec.2020 | D65 | (0.708, 0.292) | (0.170, 0.797) | (0.131, 0.046) | 約2.0 |
| ProPhoto | D50 | (0.734699, 0.265301) | (0.159597, 0.840403) | (0.036598, 0.000105) | 約1.8 |
PALとNTSCはそれぞれヨーロッパとアメリカの放送で用いられる映像信号の規格である。
色差色空間
YUV色空間
YUV色空間の誕生には白黒テレビとカラーテレビの互換性の歴史が関わる。
元々白黒テレビでは輝度\(Y\)の信号のみを利用していたが、カラーテレビの放送が始まる際に同じ信号を白黒テレビでもカラーテレビでも利用できるような仕組みが求められることとなった。
そこで、(ガンマ補正後の)\(R', G', B'\)の三色から白黒テレビ用に\(Y'\)という輝度\(Y\)に近い値を算出し、\(B'\)と\(Y'\)の差、\(R'\)と\(Y'\)の差をスケール調整した値\(U, V\)をそれぞれカラーテレビ用の追加の信号として利用することにした。こうすることで、白黒テレビは\(Y'\)の信号を使えばこれまで使っていた\(Y\)とほぼ同じ見た目を継続できるので問題ないし、カラーテレビは\(Y', U, V\)の信号を\(R', G', B'\)に変換することでカラー映像を映し出すことができるようになる。
ルーマ
\(Y'\)はルーマと呼ばれる値であり、YUVが使われているヨーロッパの放送用規格PALが準拠するRec.601では次のように定義される。
\begin{align} Y' = 0.299R' + 0.587G' + 0.114B' \end{align}
この係数の由来はNTSCにある。NTSCではRGBからXYZへの変換行列は以下のようになる。
\begin{align} \begin{pmatrix} X \\ Y \\ Z \\ \end{pmatrix} = \begin{pmatrix} 0.607 & 0.174 & 0.200 \\ 0.299 & 0.587 & 0.114 \\ 0.000 & 0.066 & 1.116 \\ \end{pmatrix} \begin{pmatrix} sR \\ sG \\ sB \\ \end{pmatrix} \end{align}
本来輝度\(Y\)を求めるには、\(R'G'B'\)のガンマ補正を外してから次のように計算する必要がある。しかし、ルーマの計算ではガンマ補正を外す過程を省略してガンマ補正後の値のまま係数を掛けた値を用いる。
\begin{align} Y = 0.299R + 0.587G + 0.114B \end{align}
色差
\(U, V\)はそれぞれルーマとB、ルーマとRの色差信号である。その値は\(R', G', B' \in [0, 1]\)としたときに、
\begin{align} -\frac{1}{3} \leq Y' \pm \sqrt{U^2+V^2} \leq \frac{4}{3} \end{align}
となり、最大値・最小値がそれぞれ2点で成り立つように定められる。
\(Y', U, V\)を次のように置いて、この条件を満たすように係数\(\alpha_u, \alpha_v\)を求める。
\begin{align} &\begin{cases} Y' = K_R R' + K_G G' + K_B B' \\ U = \alpha_u \tilde{U} \\ V = \alpha_v \tilde{V} \\ \end{cases} \\ &\begin{cases} \tilde{U} = B'-Y' \\ \tilde{V} = R'-Y' \\ \end{cases} \end{align}
ここで、\(K_R=0.299, K_G=0.587, KB_B=0.114\)。
\(K_R+K_G+K_B=1\)であることから\(Y'\)は\([0, 1]\)の範囲の値を取り、更に\(Y', U, V\)はそれぞれ独立であるので、不等式の片方だけを調べれば良いことになる。
\begin{align} & Y' + \sqrt{\alpha_u^2 \tilde{U}^2+\alpha_v^2 \tilde{V}^2} \leq \frac{4}{3} \\ \Leftrightarrow & \alpha_u^2 \tilde{U}^2+\alpha_v^2 \tilde{V}^2 \leq \left( \frac{4}{3} - Y' \right)^2 \\ \Leftrightarrow & \left( - K_R R' - K_G G' + (1-K_B) B' \right)^2 \alpha_u^2 + \left( (1-K_R) R' - K_G G' - K_B B' \right)^2 \alpha_v^2 \leq \left( \frac{4}{3} - K_R R' - K_G G' - K_B B' \right)^2 \\ \end{align}
\(R'G'B'\)色空間の8つの頂点\((R',G',B')=(0,0,0),(0,0,1),(0,1,0), ... , (1,1,1)\)がこの式を満たすならば、その中間色である全ての色が条件をみたすことがわかる。
特に、\((R',G',B')=(0,0,0), (1,1,1)\)のときは\(U=V=0\)となることから上記の式を満たすことは自明。残りの6つの頂点について調べれば良い。
- \((R',G',B')=(1, 0, 0)\)
\begin{align} K_R^2 \alpha_u^2 + (1-K_R)^2 \alpha_v^2 \leq \left( \frac{4}{3} - K_R \right)^2 \end{align}
- \((R',G',B')=(0, 1, 0)\)
\begin{align} K_G^2 \alpha_u^2 + K_G^2 \alpha_v^2 \leq \left( \frac{4}{3} - K_G \right)^2 \end{align}
- \((R',G',B')=(0, 0, 1)\)
\begin{align} (1-K_B)^2 \alpha_u^2 + K_B^2 \alpha_v^2 \leq \left( \frac{4}{3} - K_B \right)^2 \end{align}
- \((R',G',B')=(1, 1, 0)\)
\begin{align} & (1-K_B)^2 \alpha_u^2 + K_B^2 \alpha_v^2 \\ = & (K_R+K_G)^2 \alpha_u^2 + (1-K_R-K_G)^2 \alpha_v^2 \leq \left( \frac{4}{3}-K_R-K_G \right)^2 \end{align}
- \((R',G',B')=(0, 1, 1)\)
\begin{align} & K_R^2 \alpha_u^2 + (1-K_R)^2 \alpha_v^2 \\ = & (1-K_G+K_B)^2 \alpha_u^2 + (K_G+K_B)^2 \alpha_v^2 \leq \left( \frac{4}{3}-K_G-K_B \right)^2 \end{align}
- \((R',G',B')=(1, 0, 1)\)
\begin{align} & K_G^2 \alpha_u^2 + K_G^2 \alpha_v^2 \\ = & (1-K_R+K_B)^2 \alpha_u^2 + (1-K_R-K_B)^2 \alpha_v^2 \leq \left( \frac{4}{3}-K_R-K_B \right)^2 \end{align}
これらの内、2は6の条件を、4は3の条件を、5は1の条件を含むので、2, 4, 5を全て満たすように未知数\(\alpha_u, \alpha_v\)を求めれば良い。2, 4, 5は\(\alpha_u, \alpha_v\)に対する楕円の式になっていて、図で表すと以下のようになる。
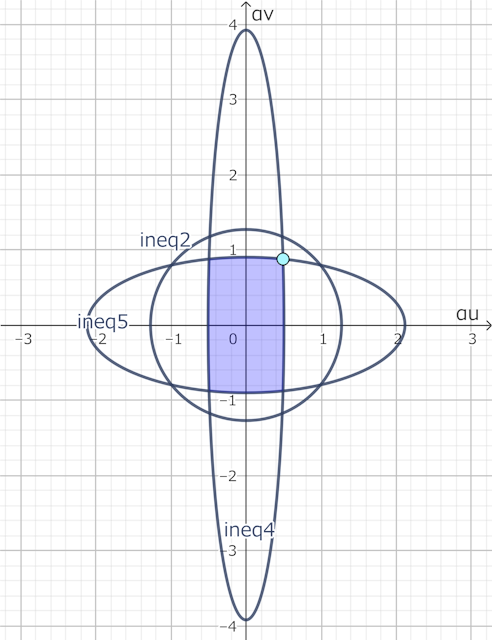
\(\alpha_u, \alpha_v\)が満たすべき不等式の範囲
これにより「4かつ5」を満たすだけで2は自動的に満たされることがわかる。
等式が2点で成り立つ必要があるので、4と5それぞれの境界の交点を求めれば良いことがわかる。4と5の等式部分より、
\begin{align} \begin{pmatrix} (1-K_B)^2 & K_B^2 \\ K_R^2 & (1-K_R)^2 \\ \end{pmatrix} \begin{pmatrix} \alpha_u^2 \\ \alpha_v^2 \\ \end{pmatrix} = \begin{pmatrix} \left( \frac{1}{3} + K_B \right)^2 \\ \left( \frac{1}{3} + K_R \right)^2 \\ \end{pmatrix} \end{align}
となるので、これを逆行列によって解くことで
\begin{align} \begin{cases} \alpha_u = 0.492111 \\ \alpha_v = 0.877283 \\ \end{cases} \end{align}
を得ることができる。
つまり、色差は次のように計算することができるということになる。(0.436, 0.615はそれぞれ\(U, V\)の最大値)
\begin{align} \begin{cases} U = 0.492111(B'-Y') = 0.436\frac{B'-Y'}{1-0.114} \\ V = 0.877283(R'-Y') = 0.615\frac{R'-Y'}{1-0.299} \\ \end{cases} \end{align}
R'G'B'からYUVへの変換は最終的に次の式になる。
\begin{align} \begin{pmatrix} Y' \\ U \\ V \end{pmatrix} = \begin{pmatrix} 0.299 & 0.587 & 0.114 \\ -0.14713 & -0.28886 & 0.436 \\ 0.615 & −0.51499 & −0.10001 \end{pmatrix} \begin{pmatrix} R' \\ G' \\ B' \end{pmatrix} \end{align}
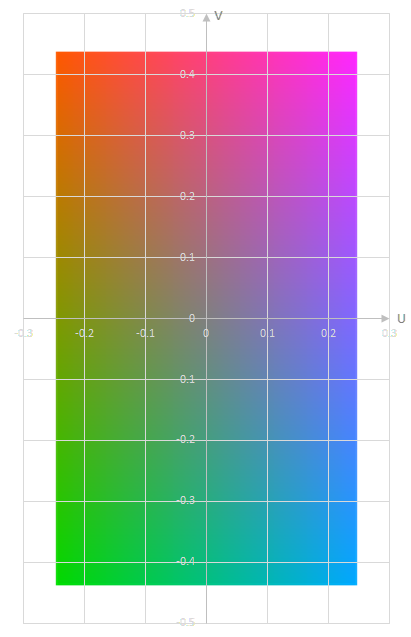
Y'=0.5の場合
YIQ色空間
YIQは人間の視覚に合わせてU, Vを33°回転させることで、人の目が敏感な色領域により多くの情報量を割いて送信することを目的とした色空間。
YUVがヨーロッパのPALで使われるのに対して、YIQはアメリカや日本で採用されているNTSCで使われている。
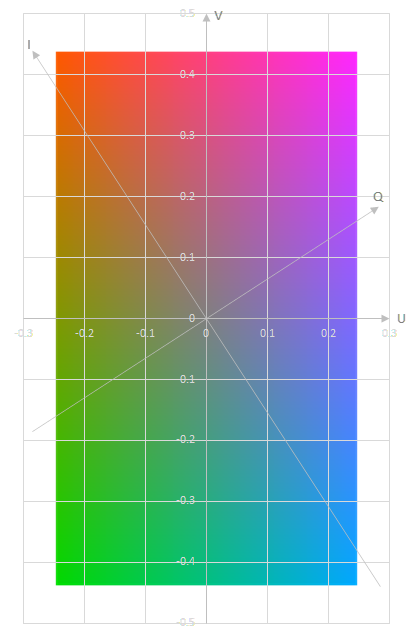
\begin{align} \begin{pmatrix} Q \\ I \\ \end{pmatrix} & = \begin{pmatrix} \cos(-33^\circ) & -\sin(-33^\circ) \\ \sin(-33^\circ) & \cos(-33^\circ) \\ \end{pmatrix} \begin{pmatrix} U \\ V \\ \end{pmatrix} \\ & = \begin{pmatrix} \cos(-33^\circ) & -\sin(-33^\circ) \\ \sin(-33^\circ) & \cos(-33^\circ) \\ \end{pmatrix} \begin{pmatrix} -0.14713 & -0.28886 & 0.436 \\ 0.615 & -0.51499 & -0.10001 \\ \end{pmatrix} \begin{pmatrix} R' \\ G' \\ B' \end{pmatrix} \\ & = \begin{pmatrix} 0.211559 & -0.522742 & 0.311191 \\ 0.595915 & -0.274583 & -0.321338 \\ \end{pmatrix} \begin{pmatrix} R' \\ G' \\ B' \end{pmatrix} \\ \end{align}
\(Y'\)はYUVと同じ。
\begin{align} \begin{pmatrix} Y' \\ I \\ Q \end{pmatrix} = \begin{pmatrix} 0.299 & 0.587 & 0.114 \\ 0.595915 & -0.274583 & -0.321338 \\ 0.211559 & -0.522742 & 0.311191 \\ \end{pmatrix} \begin{pmatrix} R' \\ G' \\ B' \end{pmatrix} \end{align}
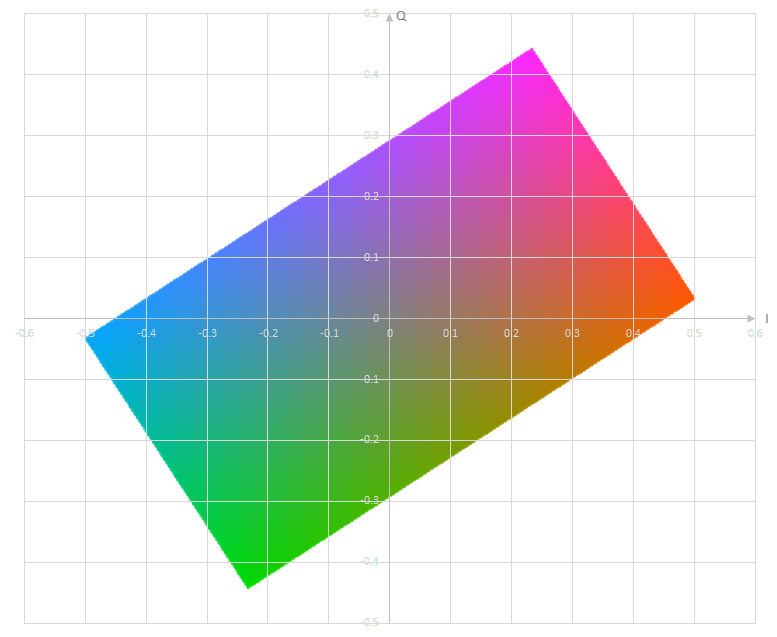
Y'=0.5の場合
YCbCr色空間
YCbCrはYUVの\(U, V\)を\([-1/2, 1/2]\)の範囲にスケール調整・平行移動した色空間。JPEGやMPEGで用いられる。YPbPrと表記されることもある。
\begin{align} \begin{cases} Cb = \frac{1}{2}\frac{B'-Y'}{1-0.114} \\ Cr = \frac{1}{2}\frac{R'-Y'}{1-0.299} \\ \end{cases} \end{align}
\(Y'\)はRec.601に従う場合(SDTV)とRec.709に従う場合(HDTV)の両方がある。\(Y'\)の定義の違いに伴い、変換行列全体がそれぞれ異なる。
- Rec.601
\begin{align} Y' = 0.299R' + 0.587G' + 0.114B' \end{align} \begin{align} \begin{pmatrix} Y' \\ Cb \\ Cr \end{pmatrix} = \begin{pmatrix} 0.299 & 0.587 & 0.114 \\ -0.1687 & -0.3313 & 0.5 \\ 0.5 & -0.4187 & -0.0813 \\ \end{pmatrix} \begin{pmatrix} R' \\ G' \\ B' \end{pmatrix} \end{align}
- Rec.709
\begin{align} Y' = 0.2126R' + 0.7152G' + 0.0722B' \end{align} \begin{align} \begin{pmatrix} Y' \\ Cb \\ Cr \end{pmatrix} = \begin{pmatrix} 0.2126 & 0.7152 & 0.0722 \\ -0.1146 & -0.3854 & 0.5 \\ 0.5 & -0.4542 & -0.0458 \\ \end{pmatrix} \begin{pmatrix} R' \\ G' \\ B' \end{pmatrix} \end{align}
円筒色空間
円筒色空間は画像処理ソフトでよく使われる色空間。CIELABのようにRGBを人間の知覚的な概念に結びつけ、直感的に扱えるようにしたもの。
HSL色空間
HSL色空間は1938年にフランスの通信技術者Georges Valensiによって設計された色空間。
HSLはそれぞれ色相(Hue)、彩度(Saturation)、輝度(Lightness)を意味する。
\begin{align} M &= \max\{R', G', B'\} \\ m &= \min\{R', G', B'\} \\ C &= M - m \\ H &= \begin{cases} 0 & (C = 0) \\ 60\frac{G'-B'}{C} & (M=R' \land G' \geq B') \\ 60\left(\frac{B'-R'}{C} + 2\right) & (M=G') \\ 60\left(\frac{R'-G'}{C} + 4\right) & (M=B') \\ 60\left(\frac{G'-B'}{C} + 6\right) & (M=R \land G' < B') \\ \end{cases} \\ L &= \frac{M+m}{2} \\ S_L &= \frac{M-L}{\min\{L, 1-L\}} \end{align}
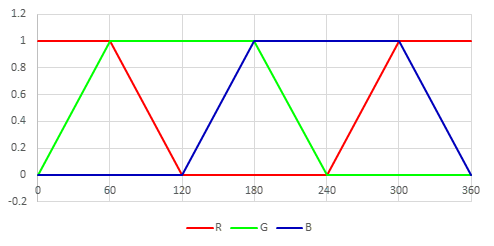
L=1/2, S=1のときのHに対するR'G'B'の挙動
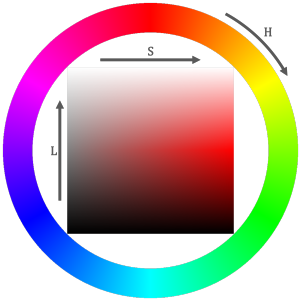
HSL色空間
HSV色空間
HSV色空間は1978年にアメリカのCG技術者Alvy Ray Smithが発表した色空間。
HSVはそれぞれ色相(Hue)、彩度(Saturation)、明度(Value)を意味する。
Hの定義はHSL空間と同じで、VとSは以下のように定義される。
\begin{align} V &= M \\ S_V &= \frac{C}{V} \end{align}

HSV色空間
上記の定義では円筒の色空間になるが、HSVは\(S_V := C\)として円錐の色空間として表現するのも一般的。