シグモイド型関数から導かれる確率分布・活性化関数・損失関数
目次
シグモイド型関数
シグモイド型関数(sigmoid function)あるいはシグモイド曲線(sigmoid curve)は、グラフがS字の形状になる関数の総称である。
この投稿では、シグモイド型関数の中でも特に次の条件に当てはまる関数\(f(x)\)について調べる。
- 広義単調増加: \(x < y \Rightarrow f(x) \leq f(y)\)
- 奇関数: \(f(-x) = -f(x)\)
- \((0,\infty)\)の範囲で上に凸
- \(f(x)\rightarrow \pm 1 \quad (x\rightarrow\pm\infty)\)
- (可能な限り) \(f'(0)=1\)
これらの性質から、\(f(x)\in[-1,1]\)が成り立つ。
\(f(x)\)を\([0,1]\)などの異なる範囲にスケール調整した関数もシグモイド型関数と呼ばれる。ここでは\([-1,1]\)の範囲のものを\(f(x)\)と表し、\([0,1]\)の範囲のものを\(g(x)=(1+f(x))/2\)と表すことにする。
tanh (ロジスティック関数)
双曲線正接関数(hyperbolic tangent) \(f(x)=\tanh(x)\)は、最も基本的なシグモイド型関数である。
\begin{align} f(x) = \tanh(x) := \frac{e^x-e^{-x}}{e^x+e^{-x}} \end{align}
\(f(x)\)をスケール調整した\(g(x)=\sigma(2x)\)はロジスティック関数と呼ばれる。あるいは、この関数を特にシグモイド関数と呼ぶ場合もある。
ロジスティック関数は機械学習の活性化関数に用いられることがある。
\begin{align} g(x) &= \frac{1}{2}\left(1+f(x)\right) \\ &= \frac{1}{2}\left(1+\frac{e^x-e^{-x}}{e^x+e^{-x}}\right) \\ &= \frac{e^x}{e^x+e^{-x}} \\ &= \frac{1}{1+e^{-2x}} \\ &=: \sigma(2x) \\ \end{align}
ロジスティック関数に\(x\)を掛けると、SwishあるいはSiLU(Sigmoid Linear Unit)と呼ばれる活性化関数になる。
\begin{align} xg(x) &= x\sigma(2x) \\ &= \frac{1}{2}\frac{2x}{1+e^{-2x}} \\ &= \frac{1}{2}\mathrm{Swish}(2x) \\ \end{align}
微分
\(g(x)=(1+f(x))/2\)は、
- 広義単調増加
- \(g(x)\rightarrow0 \quad (x\rightarrow-\infty)\)
- \(g(x)\rightarrow1 \quad (x\rightarrow \infty)\)
を満たすので、累積分布関数と同じ性質を持つことがわかる。したがって、\(g(x)\)の微分\(p(x)=g'(x)=f'(x)/2\)は確率密度関数になる。
この例の場合、\(p(x)=f'(x)/2\)はロジスティック分布として知られる分布の確率密度関数になる。
\begin{align} p(x) &= \frac{1}{2}f'(x) \\ &= \frac{1}{2}\left( \frac{e^x+e^{-x}}{e^x+e^{-x}} - \frac{(e^x-e^{-x})^2}{(e^x+e^{-x})^2} \right) \\ &= \frac{1}{2}\left( \frac{e^{2x}+2+e^{-2x}}{(e^x+e^{-x})^2} - \frac{e^{2x}-2+e^{-2x}}{(e^x+e^{-x})^2} \right) \\ &= \frac{2}{(e^x+e^{-x})^2} \\ &= \frac{2e^{-2x}}{(1+e^{-2x})^2} \\ \end{align}
この分布の平均は\(0\)。
分散については、
\begin{align} \mathbb{E}(x^2) &= \int_{-\infty}^\infty x^2p(x) dx \\ &= 2\int_0^\infty x^2p(x) dx \\ &= 4\int_0^\infty \frac{x^2e^{-2x}}{(1+e^{-2x})^2} dx \\ &= 4\int_0^\infty x^2e^{-2x}\left(\frac{1}{1+e^{-2x}}\right)^2 dx \\ &= 4\int_0^\infty x^2e^{-2x}\left( \sum_{n=0}^\infty (-e^{-2x})^n \right)^2 dx \\ &= 4\int_0^\infty x^2e^{-2x}\sum_{n=0}^\infty (n+1)(-e^{-2x})^n dx \\ &= 4\int_0^\infty x^2(-1)\sum_{n=1}^\infty n(-e^{-2x})^n dx \\ &= 4\sum_{n=1}^\infty n(-1)^{n-1}\int_0^\infty x^2e^{-2nx} dx \\ &= \frac{1}{2}\left( \sum_{n=1}^\infty \frac{(-1)^{n-1}}{n^2} \right) \int_0^\infty x^2e^{-x} dx \\ \end{align}
ここで、
\begin{align} \int_0^\infty x^2e^{-x} dx &= [-(x^2+2x+2)e^{-x}]_0^\infty \\ &= 2 \\ \end{align}
また、総和部分は\(x^2\)のFourier級数展開に\(x=0\)を代入した結果を用いて、\(\pi^2/12\)と等しくなることがわかる。
\begin{align} x^2 &= \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2} \cos(nx) \\ \end{align}
\begin{align} 0 &= \frac{\pi^2}{3} + \sum_{n=1}^\infty \frac{4(-1)^n}{n^2} \cos(n\cdot0) \\ &= \frac{\pi^2}{3} - 4\sum_{n=1}^\infty \frac{(-1)^{n-1}}{n^2} \\ \end{align}
したがって、この分布の分散は\(\pi^2/12\)となる。
\begin{align} \mathbb{E}(x^2) &= \frac{1}{2}\left( \sum_{n=1}^\infty \frac{(-1)^{n-1}}{n^2} \right) \int_0^\infty x^2e^{-x} dx \\ &= \frac{1}{2} \cdot \frac{\pi^2}{12} \cdot 2 \\ &= \frac{\pi^2}{12} \\ \end{align}
積分
\(f(x)\)を積分した関数\(L(x)\)は、以下のようになる。
この関数はLog-Cosh Lossと呼ばれ、2つの値の差を引数に取る\(L(x-y)\)の形で機械学習の損失関数に用いられることがある。\(f(x)\)の性質から、\(L(x)\)に漸近線がある場合その傾きは-1, 1になることがわかる。
\begin{align} L(x) &= \int_0^x f(x) dx \\ &= \int_0^x \frac{e^x-e^{-x}}{e^x+e^{-x}} dx \\ &= \left[ \log\left( e^x+e^{-x} \right) \right]_0^x \\ &= \log\left( \frac{1}{2}\left(e^x+e^{-x}\right) \right) \\ &= \log\left(\cosh(x)\right) \\ \end{align}
次のように、\(L(x)\)を用いて\(y=0\)と\(y=x\)が漸近線となるような関数\(\psi(x)\)を構築することができる。
この例の場合、\(\psi(x)=\log\left(1+e^{2x}\right)\)はSoftplusと呼ばれる関数になる。この関数は後述の\(ReLU(x)=\max\{0,x\}\)を滑らかにしたような関数であり、ReLUと同様に機械学習の活性化関数に用いられることがある。
\begin{align} \psi(x) &:= \frac{1}{2}\left( L\left(x\right) + x - \lim_{x\rightarrow\infty} \left(L(x)-x\right) \right) \\ &= \frac{1}{2}\left( \log\left(\frac{1}{2}\left(e^x+e^{-x}\right)\right) + \log e^x - \lim_{x\rightarrow\infty} \left(\log\left(\frac{1}{2}\left(e^x+e^{-x}\right)\right) + \log e^{-x}\right) \right) \\ &= \frac{1}{2}\left( \log\left(\frac{1}{2}\left(1+e^{2x}\right)\right) - \lim_{x\rightarrow\infty} \log\left(\frac{1}{2}\left(1+e^{-2x}\right)\right) \right) \\ &= \frac{1}{2}\left( \log\left(\frac{1}{2}\left(1+e^{2x}\right)\right) - \log\left(\frac{1}{2}\left(1+0\right)\right) \right) \\ &= \frac{1}{2}\log\left(1+e^{2x}\right) \\ &= \frac{1}{2}\mathrm{Softplus}(2x) \\ \end{align}
Hardtanh
Hardtanhは次のように定義される関数。
\begin{align} f(x) = \mathrm{Hardtanh}(x) := \begin{cases} 1 \qquad &(1\leq x) \\ x \qquad &(-1\leq x\leq1) \\ -1 \qquad &(x\leq-1) \end{cases} \end{align}

微分
\(f(x)/2\)の微分は一様分布になる。
\begin{align} p(x) &= \frac{1}{2} f'(x) \\ &= \begin{cases} \frac{1}{2} \qquad &(-1\leq x\leq1) \\ 0 \qquad &(otherwise) \end{cases} \end{align}
平均は\(0\)、分散は\(1/3\)となる。
\begin{align} \mathbb{E}(x^2) &= \int_{-1}^1 \frac{x^2}{2} dx \\ &= \int_0^1 x^2 dx \\ &= \frac{1}{3} \\ \end{align}
積分
\(f(x)\)の積分は次のようになる。
この関数はHuber LossあるいはSmooth L1 Lossと呼ばれる損失関数である。
\begin{align} L(x) &= \int_0^x f(x) dx \\ &= \begin{cases} \frac{x^2}{2} \qquad &(-1\leq x\leq1) \\ |x|-\frac{1}{2} \qquad &(otherwise) \end{cases} \end{align}

Softplusと類似した関数へは次のように変形できる。
\begin{align} \psi(x) &:= \frac{1}{2}\left( L\left(x\right) + x - \lim_{x\rightarrow\infty} \left(L(x)-x\right) \right) \\ &= \frac{1}{2}\left( L\left(x\right) + x - \left(-\frac{1}{2}\right) \right) \\ &= \begin{cases} \frac{x^2+2x+1}{4} = \left(\frac{1+x}{2}\right)^2 \qquad &(-1\leq x\leq1) \\ \frac{|x|+x}{2} = \mathrm{ReLU}(x) \qquad &(otherwise) \end{cases} \end{align}
erf
誤差関数は次のように定義される関数。
\begin{align} f(x) = \mathrm{erf}(x) := \frac{2}{\sqrt{\pi}} \int_0^x e^{-x^2} dx \end{align}
このままでは\(f'(0)=1\)とならないので、スケール調整する。
\begin{align} f(x) = \mathrm{erf}\left(\frac{\sqrt{\pi}}{2}x\right) \end{align}
\(g(x)=(1+f(x))/2\)に\(x\)を掛けると、GELU(Gaussian Error Linear Unit)と呼ばれる活性化関数になる。
\begin{align} \phi(x) &= \frac{x}{2}\left(1+f(x)\right) \\ &= \frac{x}{2}\left(1+\mathrm{erf}\left(\frac{\sqrt{\pi}}{2}x\right)\right) \\ &= \sqrt{\frac{2}{\pi}}\frac{\sqrt{\frac{\pi}{2}}x}{2}\left(1+\mathrm{erf}\left(\frac{\sqrt{\frac{\pi}{2}}x}{\sqrt{2}}\right)\right) \\ &= \sqrt{\frac{2}{\pi}}\mathrm{GELU}\left(\sqrt{\frac{\pi}{2}}x\right) \end{align}
誤差関数を含む\(\mathrm{GELU}(x)=\frac{x}{2}\left(1+\mathrm{erf}(\frac{x}{\sqrt{2}})\right)\)は計算にコストがかかるので、GELUの論文では以下のようなロジスティック関数と多項式の合成関数による近似が紹介されている。
これらの係数は、\(\mathrm{erf}(x/\sqrt{2})\)と\(\tanh(ax)\)との差の最大値、あるいは\(\mathrm{erf}(x/\sqrt{2})\)と\(\tanh(a_1x+a_2x^3)\)との差の最大値(つまり\(L^\infty\)距離)が最小化されるように選択されている。
\begin{align} \mathrm{GELU}(x) &= \frac{x}{2}\left(1+\mathrm{erf}\left(\frac{x}{\sqrt{2}}\right)\right) \\ &\sim \frac{x}{2}\left(1+\tanh\left(\frac{1.702}{2}x\right)\right) \\ &= x\sigma(1.702x) \\ &= \frac{\mathrm{Swish}(1.702x)}{1.702} \end{align}
\begin{align} \mathrm{GELU}(x) &= \frac{x}{2}\left(1+\mathrm{erf}\left(\frac{x}{\sqrt{2}}\right)\right) \\ &\sim \frac{x}{2}\left(1+\tanh\left(\sqrt{\frac{2}{\pi}}(x+0.044715x^3)\right)\right) \\ &= x\sigma\left(2\sqrt{\frac{2}{\pi}}(x+0.044715x^3)\right) \end{align}
微分
\(f(x)/2\)の微分は平均\(0\)、分散\(2/\pi\)の正規分布になる。
\begin{align} p(x) &= \frac{1}{2} f'(x) \\ &= \frac{1}{2}\frac{\sqrt{\pi}}{2}\mathrm{erf}'\left(\frac{\sqrt{\pi}}{2}x\right) \\ &= \frac{1}{2}\frac{\sqrt{\pi}}{2}\frac{2}{\sqrt{\pi}} e^{-\left(\frac{\sqrt{\pi}}{2}x\right)^2} \\ &= \frac{1}{2} e^{-\frac{\pi x^2}{4}} \\ &= p_\mathcal{N}\left(x\middle|0,\frac{2}{\pi}\right) \\ \end{align}
積分
\(f(x)\)の積分は特に知られた形にはならない。
\begin{align} L(x) &= \int_0^x f(x) dx \\ &= x \mathrm{erf}\left(\frac{\sqrt{\pi}}{2}x\right) + \frac{2}{\pi}\left( e^{-\frac{\pi x^2}{4}}-1 \right) \\ \end{align}
Softplusと類似した関数も複雑な式になる。
\begin{align} \psi(x) &:= \frac{1}{2}\left( L\left(x\right) + x - \lim_{x\rightarrow\infty} \left(L(x)-x\right) \right) \\ &= \frac{1}{2}\left( L\left(x\right) + x - \left(-\frac{2}{\pi}\right) \right) \\ &= \frac{1}{2}\left( x \mathrm{erf}\left(\frac{\sqrt{\pi}}{2}x\right) + \frac{2}{\pi}e^{-\frac{\pi x^2}{4}} + x \right) \\ &= \frac{x}{2}\left( \mathrm{erf}\left(\frac{\sqrt{\pi}}{2}x\right) + 1 \right) + \frac{1}{\pi}e^{-\frac{\pi x^2}{4}} \\ &= \sqrt{\frac{2}{\pi}}\mathrm{GELU}\left(\sqrt{\frac{\pi}{2}}x\right) + \frac{1}{\pi}e^{-\frac{\pi x^2}{4}} \\ \end{align}

Algebraic Sigmoid
次のような\(f(x)\)を考える。(あまり一般的ではないかもしれないが、)この関数はAlgebraic Sigmoid関数と呼ばれることがある。
\begin{align} f(x) = \frac{x}{\sqrt{1+x^2}} \end{align}
\(g(x)=(1+f(x))/2\)に\(x\)を掛けると次のような関数になる。(Squareplusについては後述)
\begin{align} \phi(x) &= \frac{x}{2}\left(1+\frac{x}{\sqrt{1+x^2}}\right) \\ &= \frac{1}{2}\left(x+\frac{1+x^2-1}{\sqrt{1+x^2}}\right) \\ &= \frac{1}{2}\left(x+\sqrt{1+x^2}-\frac{1}{\sqrt{1+x^2}}\right) \\ &= \frac{x+\sqrt{1+x^2}}{2}-\frac{1}{2\sqrt{1+x^2}} \\ &= \mathrm{Squareplus}(x)-\frac{1}{2\sqrt{1+x^2}} \\ \end{align}
微分
\(f(x)/2\)の微分はt分布の\(\nu=2\)の場合になる。
\begin{align} p(x) &= \frac{1}{2} f'(x) \\ &= \frac{1}{2}\left( \frac{1}{\sqrt{1+x^2}} - \frac{x^2}{(1+x^2)^{3/2}} \right) \\ &= \frac{1}{2}\left( \frac{1+x^2}{(1+x^2)^{3/2}} - \frac{x^2}{(1+x^2)^{3/2}} \right) \\ &= \frac{1}{2(1+x^2)^{3/2}} \\ \end{align}
平均は\(0\)だが、分散は\(\infty\)に発散する。
積分
\(f(x)\)の積分は次のようになる。
この関数はPseudo-Huber Lossと呼ばれる損失関数である。
\begin{align} L(x) &= \int_0^x f(x) dx \\ &= \sqrt{1+x^2} - 1 \\ \end{align}
Softplusと類似した関数へは次のように変形できる。この関数もあまり知られていないがSquareplusと名付けられている。
\begin{align} \psi(x) &:= \frac{1}{2}\left( L\left(x\right) + x - \lim_{x\rightarrow\infty} \left(L(x)-x\right) \right) \\ &= \frac{1}{2}\left( \sqrt{1+x^2} - 1 + x - \lim_{x\rightarrow\infty} \left(\sqrt{1+x^2} - 1 - x\right) \right) \\ &= \frac{1}{2}\left( \sqrt{1+x^2} - 1 + x - \lim_{x\rightarrow\infty} \left(\frac{1}{\sqrt{1+x^2}+x} - 1\right) \right) \\ &= \frac{1}{2}\left( \sqrt{1+x^2} - 1 + x - \left(-1\right) \right) \\ &= \frac{1}{2}\left( \sqrt{1+x^2} + x \right) \\ \end{align}
arctan
arctanはtan (正接関数)の逆関数。
\begin{align} f(x) = \arctan(x) := \tan^{-1}(x) \end{align}
このままでは\(\lim_{x\rightarrow\pm\infty}f(x)=\pm1\)とならないので、スケール調整する。
\begin{align} f(x) = \frac{2}{\pi}\arctan\left(\frac{\pi}{2}x\right) \end{align}
微分
\(f(x)/2\)の微分はCauchy分布になる。
\begin{align} p(x) &= \frac{1}{2} f'(x) \\ &= \frac{1}{2} \arctan'\left(\frac{\pi}{2}x\right) \\ &= \frac{1}{2} \frac{1}{1+\left(\frac{\pi}{2}x\right)^2} \\ &= \frac{1}{\pi} \frac{2/\pi}{\left(2/\pi\right)^2+x^2} \\ \end{align}
Cauchy分布は分散どころか平均すらも発散して定義できない。
積分
\(f(x)\)の積分は特に知られた形にはならない。
\begin{align} L(x) &= \int_0^x f(x) dx \\ &= \frac{2}{\pi}x\arctan\left(\frac{\pi}{2}x\right) - \frac{2}{\pi^2}\log\left(1+\left(\frac{\pi}{2}x\right)^2\right) \end{align}
この\(L(x)\)には漸近線が存在しないので、Softplusと類似した関数を構築することはできない。
Softsign
Softsignは次のように定義される関数。
\begin{align} f(x) = \mathrm{Softsign}(x) &:= \frac{x}{1+|x|} \\ &= \begin{cases} 1-\frac{1}{1+x} \qquad &(0\leq x) \\ -1+\frac{1}{1-x} \qquad &(x\leq0) \end{cases} \end{align}

\(g(x)=(1+f(x))/2\)に\(x\)を掛けると次のような関数になる。
\begin{align} \phi(x) &= \frac{x}{2}\left(1+f(x)\right) \\ &= \frac{x}{2}\left(1+\frac{x}{1+|x|}\right) \\ &= \frac{1}{2}\left(x+\frac{|x|^2}{1+|x|}\right) \\ &= \frac{1}{2}\left(x+\frac{(|x|-1)(|x|+1)+1}{1+|x|}\right) \\ &= \frac{1}{2}\left(x+|x|-1+\frac{1}{1+|x|}\right) \\ &= \frac{1}{2}\left(2\mathrm{ReLU}(x)-\frac{|x|}{1+|x|}\right) \\ &= \mathrm{ReLU}(x)-\frac{|x|}{2(1+|x|)} \\ \end{align}
微分
\(f(x)/2\)の微分は次のような確率分布になる。
\begin{align} p(x) &= \frac{1}{2} f'(x) \\ &= \frac{1}{2} \left( \frac{1}{1+|x|} - \frac{x\mathrm{sign}(x)}{(1+|x|)^2} \right) \\ &= \frac{1}{2} \left( \frac{1+|x|}{(1+|x|)^2} - \frac{|x|}{(1+|x|)^2} \right) \\ &= \frac{1}{2} \frac{1}{(1+|x|)^2} \\ \end{align}
平均も分散も発散して定義不可能。
積分
\(f(x)\)の積分は特に知られた形にはならない。
\begin{align} L(x) &= \int_0^x f(x) dx \\ &= |x|-\log(1+|x|) \end{align}
この\(L(x)\)には漸近線が存在しないので、Softplusと類似した関数を構築することはできない。
sign
符号関数は次のように定義される関数。
\begin{align} f(x) = \mathrm{sign}(x) &:= \begin{cases} 1 \qquad &(0<x) \\ 0 \qquad &(x=0) \\ -1 \qquad &(x<0) \end{cases} \end{align}
スケール調整するとHeavisideの階段関数になる。
\begin{align} g(x) = \frac{1}{2}\left(1+f(x)\right) &:= \begin{cases} 1 \qquad &(0<x) \\ 0 \qquad &(x<0) \end{cases} \end{align}
\(g(x)=(1+f(x))/2\)に\(x\)を掛けるとReLU(Rectified Linear Unit)になる。この関数はランプ関数とも呼ばれる。
ReLUは\(\mathrm{ReLU}(x) = (x+|x|)/2 = max\{0,x\}\)などと表すこともできる。
\begin{align} \phi(x) &= \frac{x}{2}\left(1+f(x)\right) \\ &= \begin{cases} x \qquad &(0<x) \\ 0 \qquad &(x<0) \end{cases} \end{align}
微分
\(f(x)/2\)の微分はデルタ分布(Diracのデルタ関数)になる。
平均は\(0\)、分散も\(0\)となる。
積分
\(f(x)\)の積分は\(x\)の絶対値になる。
\(x,y\)の各成分の差の絶対値\(|x_i-y_i|\)を計算し、総和を取ればL1 Lossになり、平均を取ればMAE Loss(Mean Absolute Error)になる。
\begin{align} L(x) &= \int_0^x f(x) dx \\ &= |x| \end{align}
\(L(x)\)を変形すると再びReLUが得られる。
\begin{align} \psi(x) &= \frac{1}{2}\left(|x| + x\right) \\ &= \begin{cases} x \qquad &(0<x) \\ 0 \qquad &(x<0) \end{cases} \end{align}
恒等関数
シグモイド型ではないが、恒等関数についても同様に調べる。
\begin{align} f(x) = x \end{align}
積分
\(f(x)\)の積分は次のようになる。
\(x,y\)の各成分について\((x_i-y_i)^2\)を計算し、平均を取ればMSE Loss(Mean Square Error)になる。
\begin{align} L(x) = \int_0^x f(x) dx = \frac{x^2}{2} \end{align}
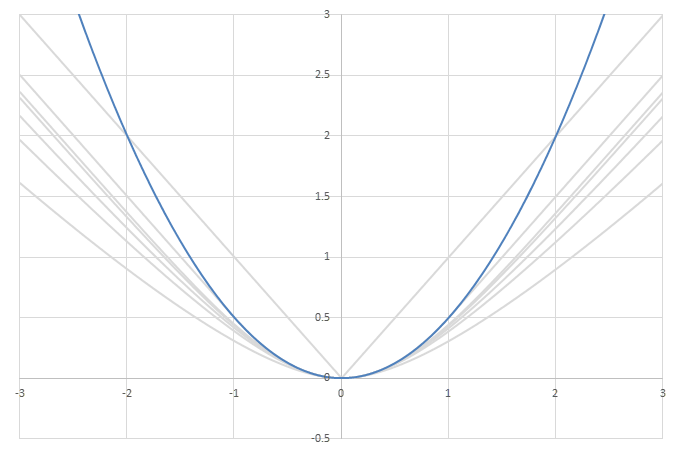
まとめ
これまでの内容を以下にまとめる。
| シグモイド型 f | 微分 p | 積分 L | Swish類 φ | Softplus類 ψ |
|---|---|---|---|---|
| Hardtanh | 一様分布 | Huber Loss | (省略) | (省略) |
| erf | 正規分布 | (省略) | GELU | (省略) |
| tanh | ロジスティック分布 | Log-Cosh Loss | Swish | Softplus |
| Algebraic Sigmoid | t分布 (ν=2) | Pseudo-Huber Loss | \(\mathrm{Squareplus}(x)-\frac{1}{2\sqrt{1+x^2}}\) | Squareplus |
| arctan | Cauchy分布 | (省略) | (省略) | - |
| Softsign | \(\frac{1}{2(1+|x|)^2}\) | \(|x|-\log(1+|x|)\) | \(\mathrm{ReLU}(x)-\frac{|x|}{2(1+|x|)}\) | - |
| sign | デルタ分布 | L1 Loss (MAE Loss) | ReLU | ReLU |
| 恒等関数 | - | MSE Loss | - | - |
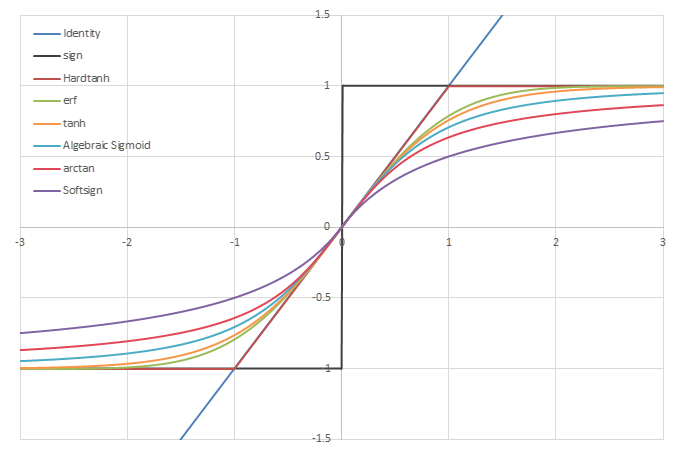
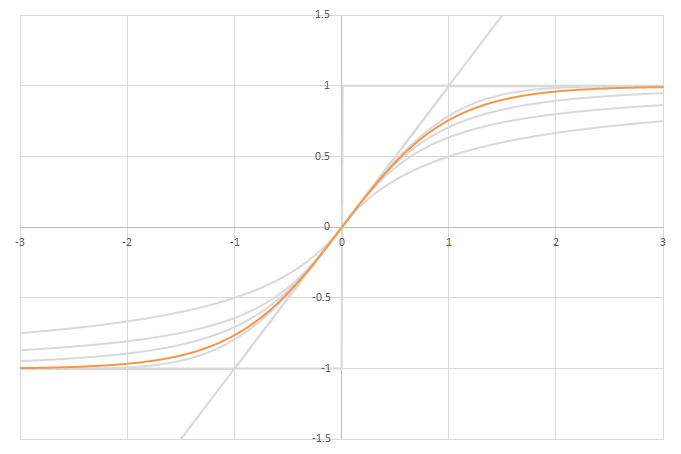
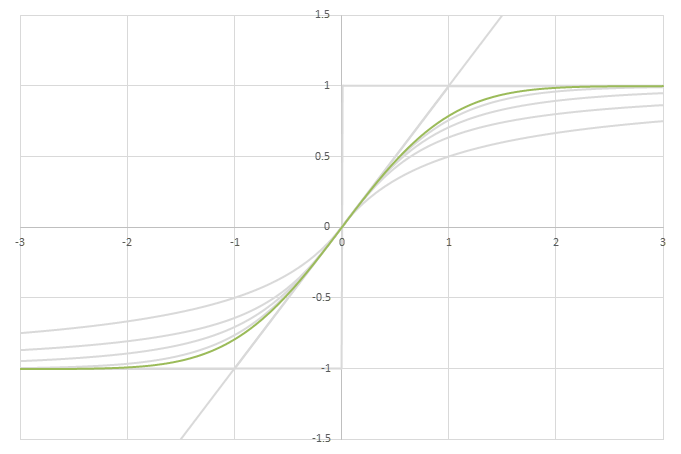
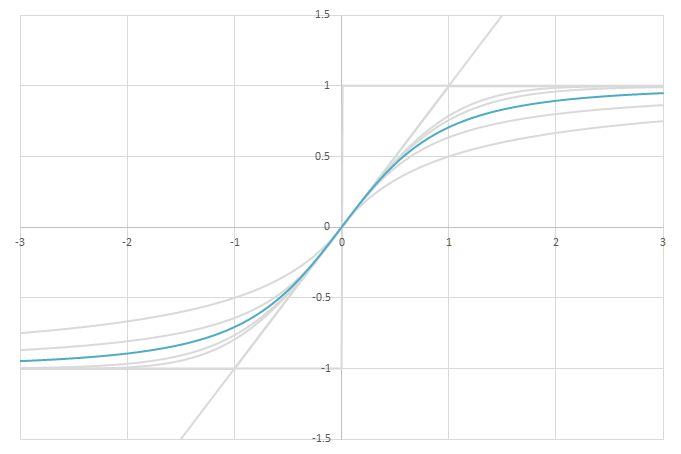
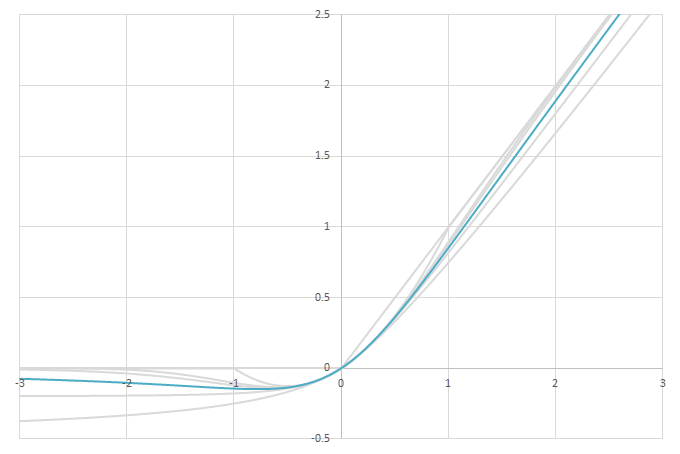
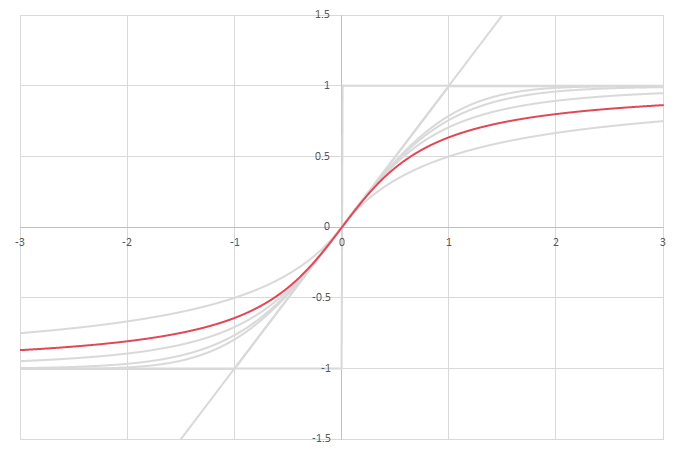
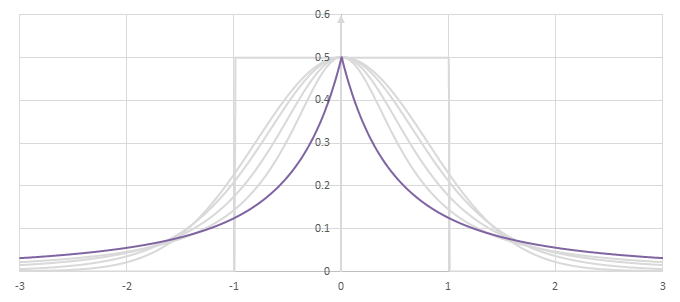
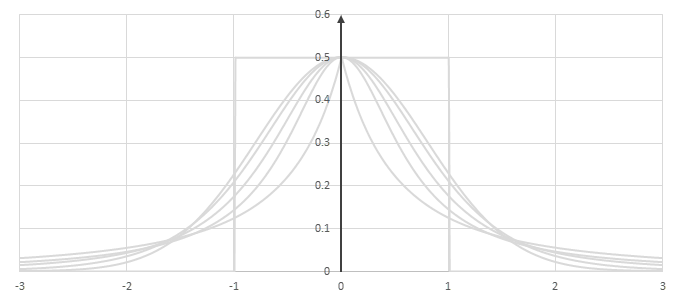
シグモイド型関数\(f(x)\)の比較
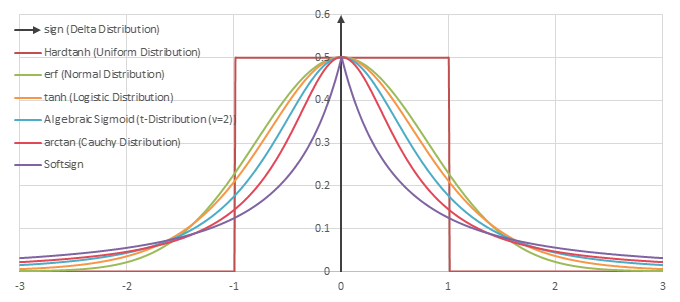
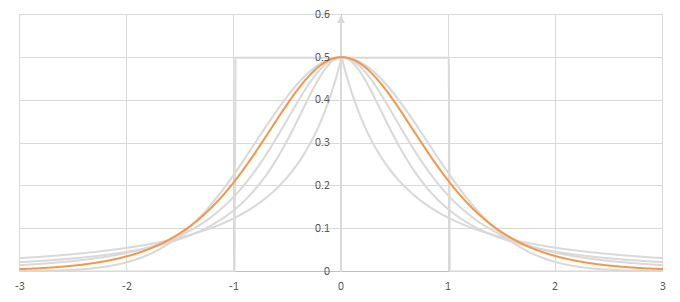
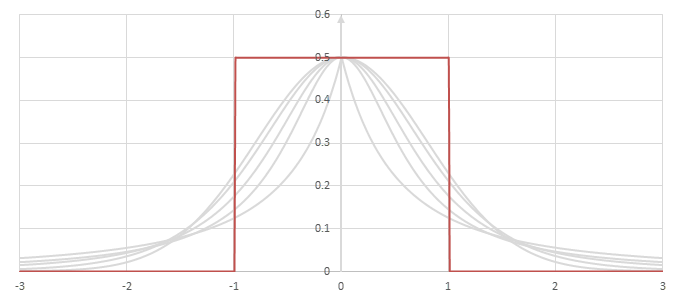
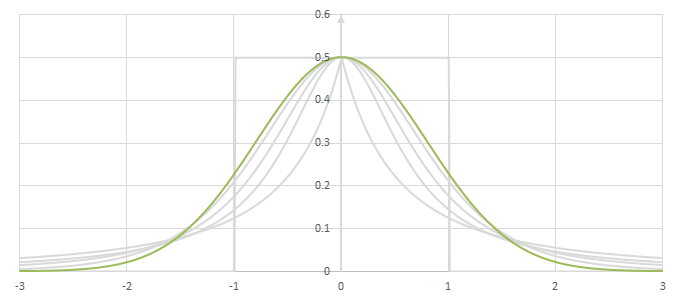
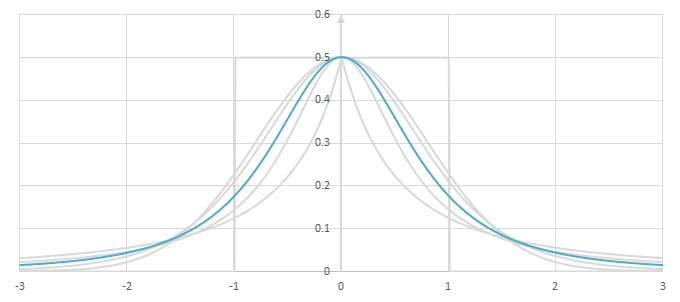
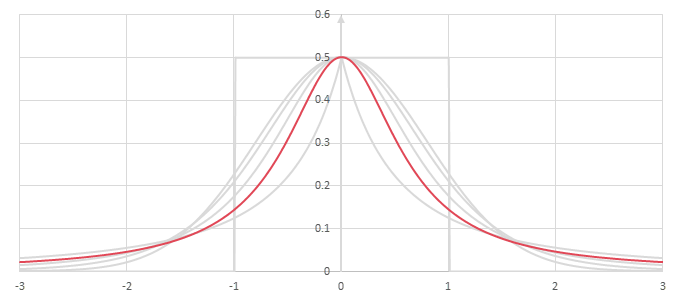
シグモイド型関数の微分\(p(x)=f'(x)/2\)の比較
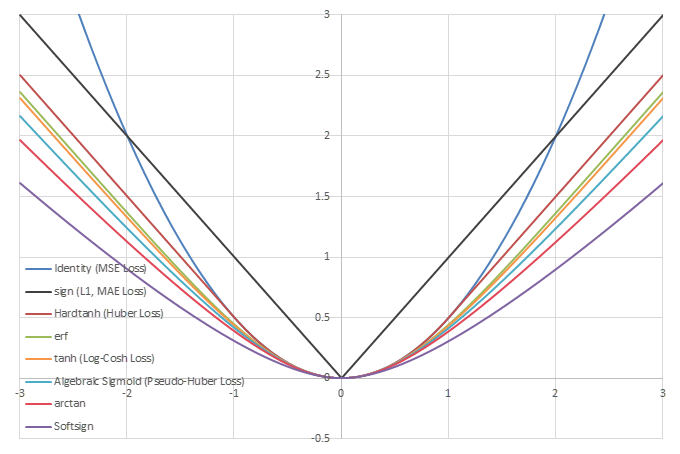
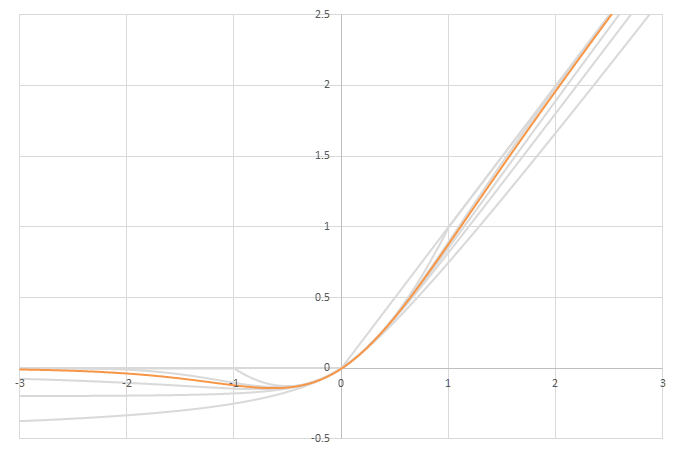
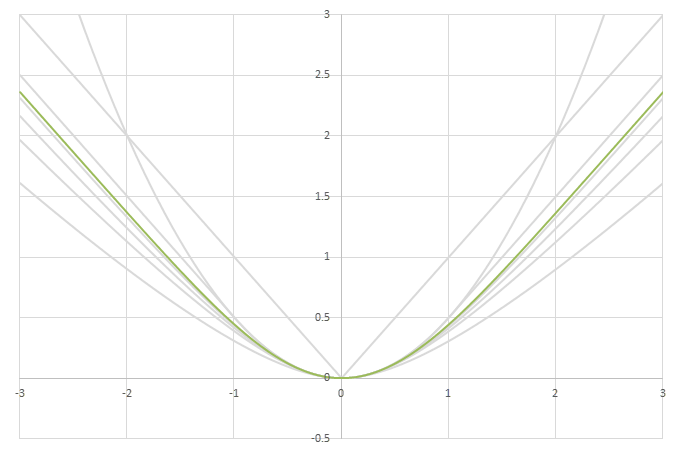
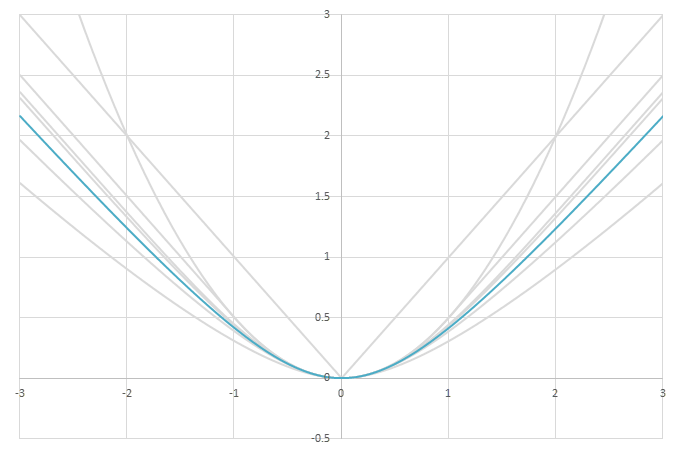
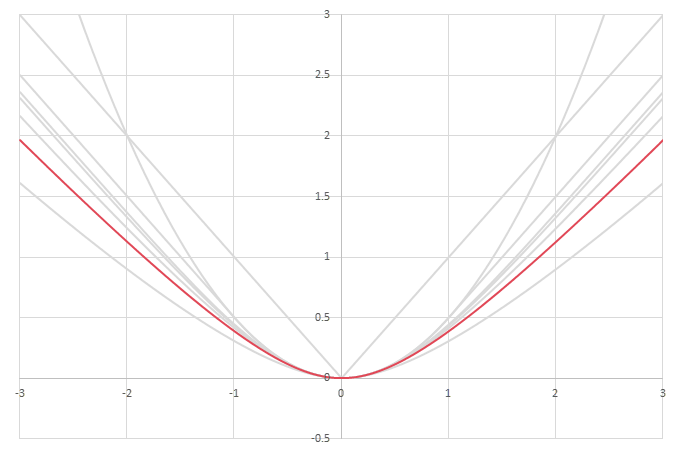
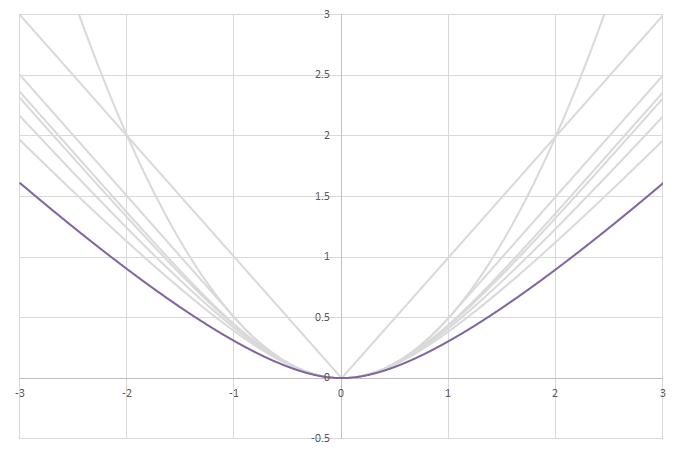
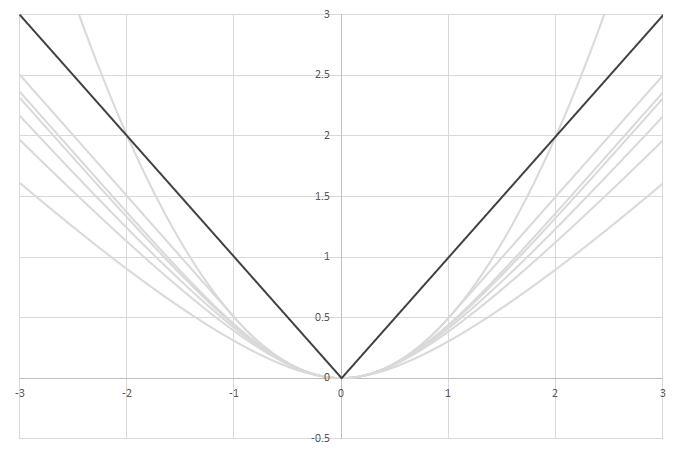
シグモイド型関数の積分\(L(x)=\int_0^xf(x)dx\)の比較
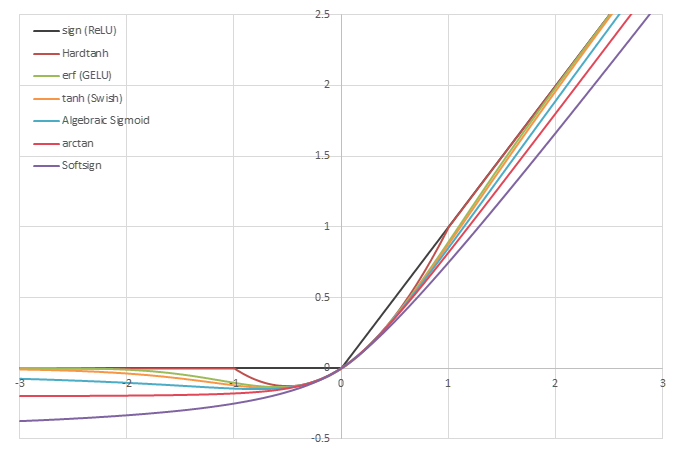
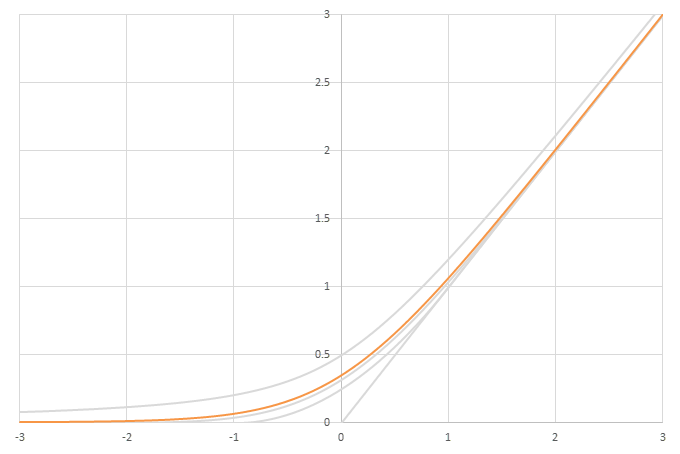
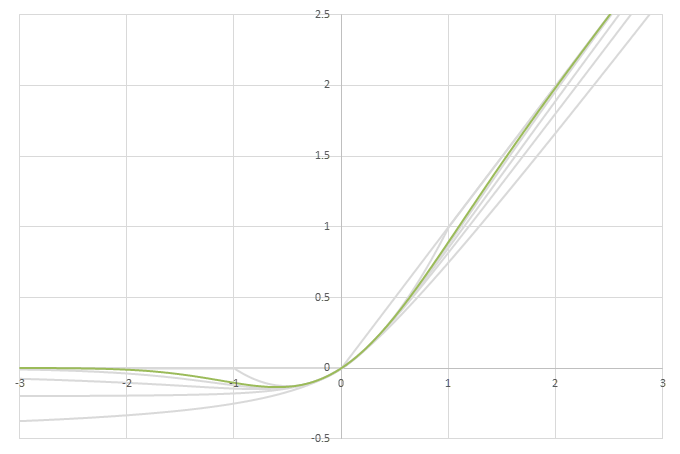
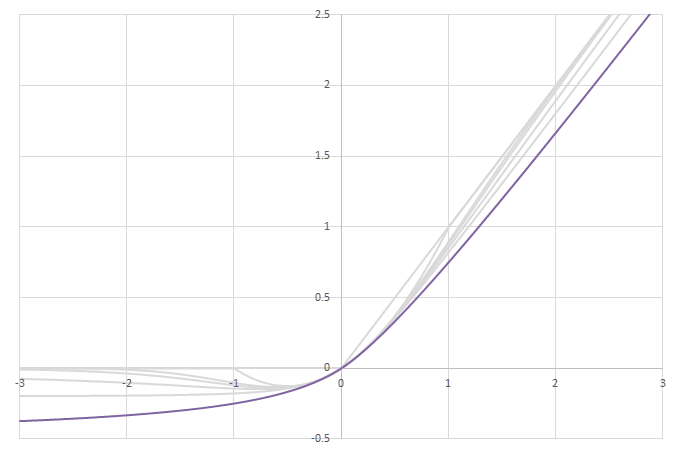
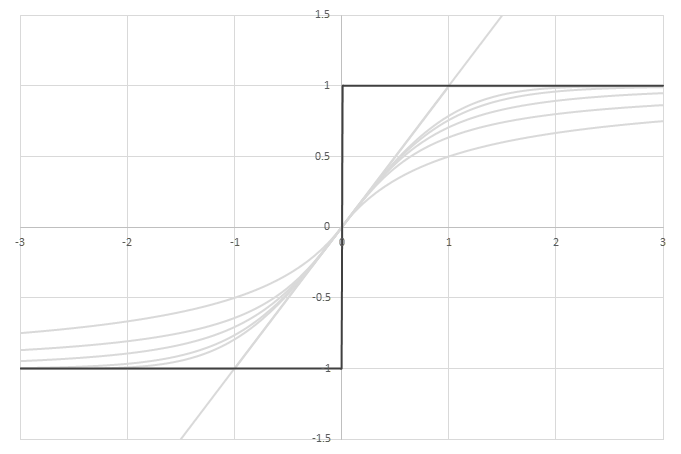
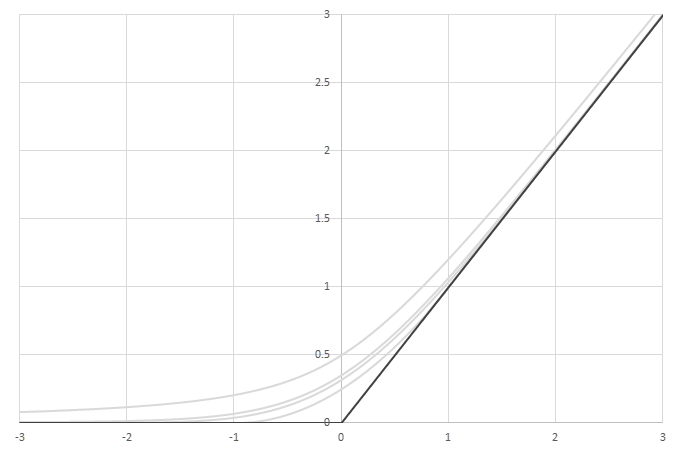
シグモイド型関数から得られるSwishに類似した関数
\(\phi(x)=\frac{x}{2}(1+f(x))\)の比較
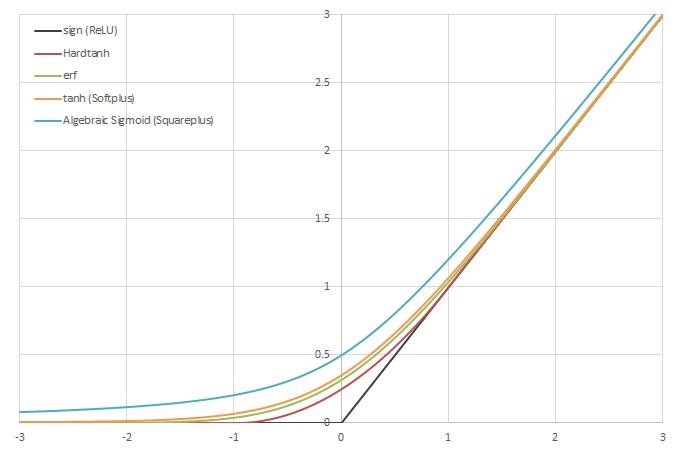
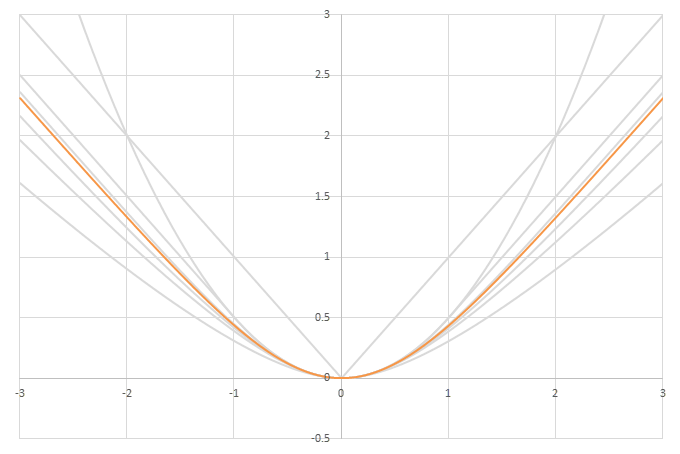
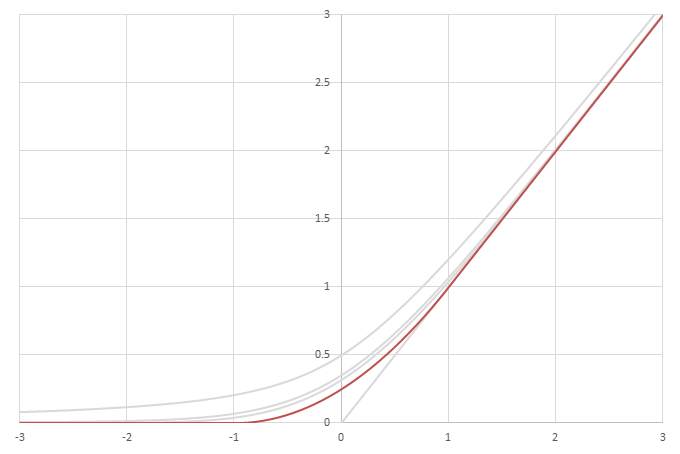
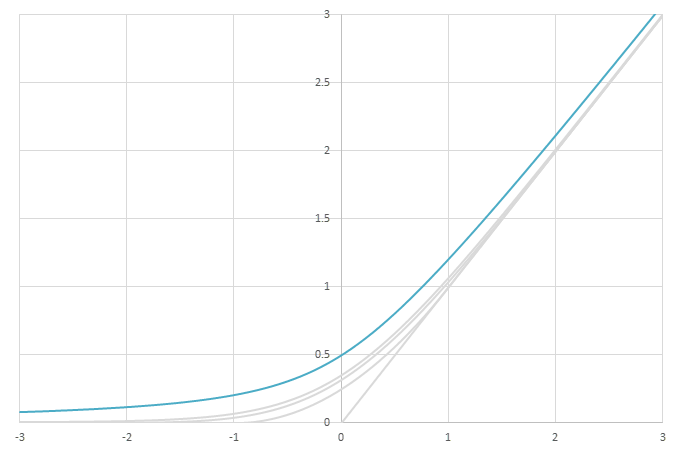
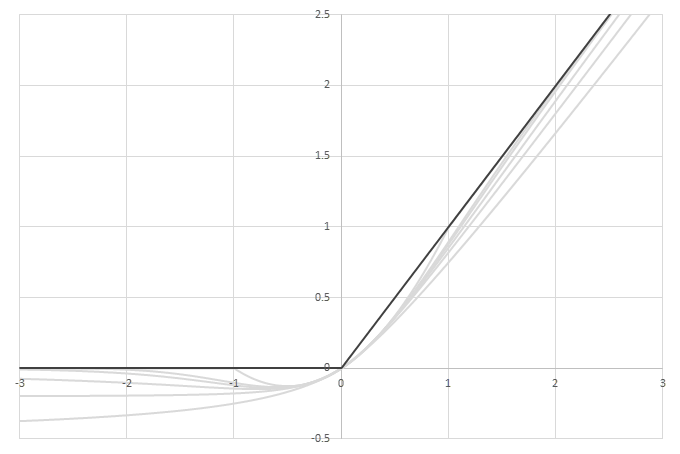
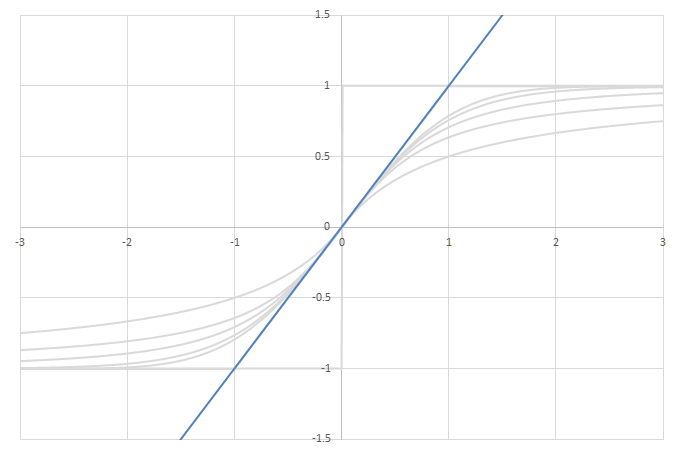
シグモイド型関数の積分から得られるSoftplusに類似した関数
\(\psi(x) = \frac{1}{2}\left( L\left(x\right) + x - \lim_{x\rightarrow\infty} \left(L(x)-x\right) \right)\)の比較
参考
シグモイド型関数
- Sigmoid function - Wikipedia
- Gelu関数+Gauss分布=Softplus関数? #機械学習 - Qiita
- ゼロ近傍で傾きを持ち、±∞で±1か±π/2になる関数 · GitHub
- [2202.07425] Algebraic function based Banach space valued ordinary and fractional neural network approximations
活性化関数
- Rectifier (neural networks) - Wikipedia
- [1811.03378] Activation Functions: Comparison of trends in Practice and Research for Deep Learning
- 活性化関数一覧 (2020) #Python - Qiita
- NumPyだけで本格的なMLPクラスを実装Ⅱ:いろいろな活性化関数とその導関数 【Deep Learning アドベントカレンダー2020】 | AGIRobots Blog
- E. Page - Approximations to the cumulative normal function and its inverse for use on a pocket calculator.