正規分布の標本分散が従う分布
本投稿では、正規分布から独立に取り出されたn個の値(=標本)について、その平均や分散がどのような分布に従っているのかを確かめる。
キーワード:
- Distribution of sample variance from normal distribution
- Relationship between chi-squared distribution and normal distribution
目次
前提
平均\(\mu\)・分散\(\sigma^2\)の正規分布から独立に取り出された\(n\)個の値(=標本)を\(\{x_i\}_{i=1}^n\)と表す。
\begin{align} x_i \sim \mathcal{N}(\mu,\sigma^2) \end{align}
また、\(z_i\)を
\begin{align} z_i := \frac{x_i-\mu}{\sigma} \sim \mathcal{N}(0,1) \end{align}
と定義する。
標本平均
標本平均は次のように定義される。
\begin{align} \bar{x} := \frac{1}{n}\sum_{i=1}^n x_i \end{align}
このとき、正規分布の再生性から\(\sum x_i\)は\(\mathcal{N}(n\mu,n\sigma^2)\)に従うので、次の関係が成り立つ。
\begin{align} n\bar{x} &= \sum_{i=1}^n x_i \\ &\sim \mathcal{N}(n\mu,n\sigma^2) \\ \end{align}
ここで、
\begin{align} p(\bar{x}) &= np(n\bar{x}) \\ \end{align}
なので(後述)、
\begin{align} p(\bar{x}) &= np(n\bar{x}) \\ &= n\frac{1}{\sqrt{2\pi n\sigma^2}}\exp\left(-\frac{(n\bar{x}-n\mu)^2}{2n\sigma^2}\right) \\ &= \frac{1}{\sqrt{2\pi \frac{\sigma^2}{n}}}\exp\left(-\frac{(\bar{x}-\mu)^2}{2\frac{\sigma^2}{n}}\right) \\ &= p_\mathcal{N}\left(\bar{x}\middle|\mu,\frac{\sigma^2}{n}\right) \\ \end{align}
となり、標本平均が従う分布は次の正規分布になることがわかる。
\begin{align} \bar{x} = \mathcal{N}\left(\mu,\frac{\sigma^2}{n}\right) \end{align}
確率変数\(x\)が確率密度関数\(p_x(x)\)で表される分布に従っているとする。
\(a\in \mathbb{R}\)に対して\(y=ax\)として、\(y\)の確率密度関数を\(p_y(y)\)と表す。
このとき、
\begin{align} p_y(y) &= \frac{d}{dz}\mathrm{Pr}(z<y) \\ &= \frac{d}{dz}\mathrm{Pr}(z<ax) \\ &= \frac{d}{dz}\mathrm{Pr}\left(\frac{z}{a}<x\right) \\ &= \frac{1}{a}\frac{d}{d\frac{z}{a}}\mathrm{Pr}\left(\frac{z}{a}<x\right) \\ &= \frac{1}{a}p_x(x) \\ &= \frac{1}{a}p_x\left(\frac{y}{a}\right) \\ \end{align}
という関係が成り立つ。
標本分散
標本分散は次のように定義される。
\begin{align} s^2 &:= \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2 \\ \end{align}
\(z_i\)を使うと次のように表現することもできる。
\begin{align} s^2 &:= \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2 \\ &= \frac{\sigma^2}{n}\sum_{i=1}^n (z_i-\bar{z})^2 \\ &= \frac{\sigma^2}{n}\sum_{i=1}^n (z_i^2-2\bar{z}z_i+\bar{z}^2) \\ &= \frac{\sigma^2}{n}\left(\sum_{i=1}^n z_i^2 - 2\bar{z}\sum_{i=1}^n z_i + \bar{z}^2\sum_{i=1}^n 1\right) \\ &= \frac{\sigma^2}{n}\left(\sum_{i=1}^n z_i^2 - 2\bar{z}n\bar{z} + \bar{z}^2n\right) \\ &= \frac{\sigma^2}{n}\sum_{i=1}^n z_i^2 - \sigma^2\bar{z}^2 \\ \end{align}
標本分散の期待値
標本分散が従う分布を具体的に調べる前に、まずは標本分散の\(\{z_i\}_{i=1}^n\)に対する期待値を簡単に確認してみよう。
\begin{align} s^2 &= \frac{\sigma^2}{n}\sum_{i=1}^n z_i^2 - \sigma^2\bar{z}^2 \\ &= \frac{\sigma^2}{n}\sum_{i=1}^n z_i^2 - \frac{\sigma^2}{n^2}\left(\sum_{i=1}^n z_i\right)^2 \\ &= \frac{\sigma^2}{n}\sum_{i=1}^n z_i^2 - \frac{\sigma^2}{n^2}\sum_{i=1}^n \sum_{j=1}^n z_iz_j \\ \end{align}
となるが、
\begin{align} \mathbb{E}_z(z_iz_j) &= \begin{cases} \mathbb{E}_{z_i}(z_i^2) = 1 &\qquad (i=j) \\ \mathbb{E}_{z_i}(z_i)\mathbb{E}_{z_j}(z_j) = 0 &\qquad (i\neq j) \\ \end{cases} \end{align}
なので、\(\mathbb{E}_z(z_iz_j) = \delta_{i,j}\)である。
これを用いると、
\begin{align} \mathbb{E}_z(s^2) &= \frac{\sigma^2}{n}\sum_{i=1}^n \mathbb{E}_z(z_i^2) - \frac{\sigma^2}{n^2}\sum_{i=1}^n \sum_{j=1}^n \mathbb{E}_z(z_iz_j) \\ &= \frac{\sigma^2}{n}\sum_{i=1}^n 1 - \frac{\sigma^2}{n^2}\sum_{i=1}^n \sum_{j=1}^n \delta_{i,j} \\ &= \frac{\sigma^2}{n}n - \frac{\sigma^2}{n^2}n \\ &= \frac{n-1}{n}\sigma^2 \\ \end{align}
となって標本分散の期待値を求めることができた。
この式を変形すると、
\begin{align} \mathbb{E}_z\left(\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2\right) &= \mathbb{E}_z\left(\frac{n}{n-1}s^2\right) \\ &= \sigma^2 \\ \end{align}
が成立し、\(\frac{n}{n-1}s^2\)は母分散\(\sigma^2\)(=\(x_i\)が従う元の分布の分散)を推定する量になっていることがわかる。
\(\frac{n}{n-1}s^2\)は不偏分散と呼ばれる。
| 名称 | 値 |
|---|---|
| 母分散 | \(\sigma^2\) |
| 標本分散 | \(s^2=\frac{1}{n}\sum_i(x_i-\bar{x})^2\) |
| 不偏分散 | \(\frac{n}{n-1}s^2=\frac{1}{n-1}\sum_i(x_i-\bar{x})^2\) |
標本分散が従う分布
前節では標本分散の期待値を導出したが、今度は標本分散が従う分布を更に具体的に調べてみる。
一般的には正規分布の標本分散が従う分布を導出するためにはCochranの定理を証明して利用する必要があるが、以下では特殊な場合のみを考えることで(Cochranの定理そのものを証明するよりも)簡単に標本分散が従う分布を導出する。
標本分散の行列による表現
\(n\)値の確率変数\(z\)を
\begin{align} z := \begin{pmatrix} z_1 \\ z_2 \\ \vdots \\ z_n \end{pmatrix} \end{align}
と定義すると、標本分散は\(z\)と行列を使って
\begin{align} s^2 &= \frac{\sigma^2}{n}\sum_{i=1}^n z_i^2 - \sigma^2\bar{z}^2 \\ &= \frac{\sigma^2}{n}\left( \sum_{i=1}^n z_i^2 - \frac{1}{n}\sum_{i=1}^n \sum_{j=1}^n z_iz_j \right) \\ &= \frac{\sigma^2}{n}\left( z^\mathrm{T}z - \frac{1}{n}z^\mathrm{T}\begin{pmatrix} 1 & \cdots & 1 \\ \vdots & \ddots & \vdots \\ 1 & \cdots & 1 \\ \end{pmatrix}z \right) \\ &= \frac{\sigma^2}{n}z^\mathrm{T}\left( I - \frac{1}{n}\begin{pmatrix} 1 & \cdots & 1 \\ \vdots & \ddots & \vdots \\ 1 & \cdots & 1 \\ \end{pmatrix} \right)z \\ \end{align}
と表すことができる。
ここで、\(A_1, A_2\)を
\begin{align} A_1 &:= \frac{1}{n}\begin{pmatrix} 1 & \cdots & 1 \\ \vdots & \ddots & \vdots \\ 1 & \cdots & 1 \\ \end{pmatrix} \\ A_2 &:= I - A_1 \\ &= \begin{pmatrix} 1-1/n & -1/n & \cdots & -1/n \\ -1/n & 1-1/n & \cdots & -1/n \\ \vdots & \vdots & \ddots & \vdots \\ -1/n & -1/n & \cdots & 1-1/n \\ \end{pmatrix} \\ \end{align}
と定めると、
\begin{align} \frac{ns^2}{\sigma^2} &= z^\mathrm{T}A_2z \\ \end{align}
とも表すことができる。したがって、
\begin{align} \sum_{i=1}^n z_i^2 &= \frac{1}{n}\sum_{i=1}^n \sum_{j=1}^n z_iz_j + \frac{ns^2}{\sigma^2} \\ &= z^\mathrm{T}A_1z + z^\mathrm{T}A_2z \\ \end{align}
という関係が導かれる。
なお、\(A_k\) (\(k=1, 2\))はそれぞれ以下の性質を満たす。
- \(A_k^\mathrm{T}=A_k\) (対称行列)
- \(A_k^2=A_k\) (冪等行列)
\(A_k\)の対角化
\(A_k\)を対角化するために、\(P\)を例えば以下のように定義する。
\begin{align} P := \begin{pmatrix} \frac{1}{\sqrt{n}} & \frac{1}{\sqrt{n}} & \frac{1}{\sqrt{n}} & \frac{1}{\sqrt{n}} & \cdots & \frac{1}{\sqrt{n}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & 0 & \cdots & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & -\frac{2}{\sqrt{6}} & 0 & \cdots & 0 \\ \frac{1}{\sqrt{12}} & \frac{1}{\sqrt{12}} & \frac{1}{\sqrt{12}} & -\frac{3}{\sqrt{12}} & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \frac{1}{\sqrt{n^2-n}} & \frac{1}{\sqrt{n^2-n}} & \frac{1}{\sqrt{n^2-n}} & \frac{1}{\sqrt{n^2-n}} & \cdots & -\frac{n-1}{\sqrt{n^2-n}} \\ \end{pmatrix} \end{align}
このとき、
\begin{align} PP^\mathrm{T} = I \end{align}
なので、\(P^{-1}=P^\mathrm{T}\)となる。(このように\(PP^\mathrm{T}=I\)となる行列\(P\)のことを直交行列という)
\(A_1\)は\(P\)によって次のように対角化される。
\begin{align} PA_1P^{-1} &= PA_1P^\mathrm{T} \\ &= \begin{pmatrix} \frac{1}{\sqrt{n}} & \frac{1}{\sqrt{n}} & \cdots & \frac{1}{\sqrt{n}} \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \\\\ \end{pmatrix}P^\mathrm{T} \\ &= \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \\\\ \end{pmatrix} \\ &=: D_1 \end{align}
また、\(A_2\)も同じ\(P\)によって次のように対角化される。
\begin{align} PA_2P^{-1} &= P(I-A_1)P^{-1} \\ &= I - PA_1P^{-1} \\ &= \begin{pmatrix} 0 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\\\ \end{pmatrix} \\ &=: D_2 \end{align}
\(D_k\)も\(A_k\)と同じように、それぞれ対称な冪等行列であり、更に\(D_1D_2=0\)が成立する。
確率変数の変換と独立性の確認
\(y^{(k)} := PA_kz\)とする。具体的には次のようになる。
\begin{align} y^{(1)} &:= PA_1z \\ &= \begin{pmatrix} \frac{1}{\sqrt{n}} & \frac{1}{\sqrt{n}} & \frac{1}{\sqrt{n}} & \frac{1}{\sqrt{n}} & \cdots & \frac{1}{\sqrt{n}} \\ 0 & 0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & 0 \\ \end{pmatrix}z = \begin{pmatrix} \sqrt{n}\bar{z} \\ 0 \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{pmatrix} \end{align}
\begin{align} y^{(2)} &:= PA_2z \\ &= (P-PA_1)z \\ &= \begin{pmatrix} 0 & 0 & 0 & 0 & \cdots & 0 \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & 0 & \cdots & 0 \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & -\frac{2}{\sqrt{6}} & 0 & \cdots & 0 \\ \frac{1}{\sqrt{12}} & \frac{1}{\sqrt{12}} & \frac{1}{\sqrt{12}} & -\frac{3}{\sqrt{12}} & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ \frac{1}{\sqrt{n^2-n}} & \frac{1}{\sqrt{n^2-n}} & \frac{1}{\sqrt{n^2-n}} & \frac{1}{\sqrt{n^2-n}} & \cdots & -\frac{n-1}{\sqrt{n^2-n}} \\ \end{pmatrix}z = \begin{pmatrix} 0 \\ \frac{1}{\sqrt{2}}\left(-z_2 + \sum_{j=1}^1z_i\right) \\ \frac{1}{\sqrt{6}}\left(-2z_3 + \sum_{j=1}^2z_i\right) \\ \frac{1}{\sqrt{12}}\left(-3z_4 + \sum_{j=1}^3z_i\right) \\ \vdots \\ \frac{1}{\sqrt{n^2-n}}\left(-nz_n + \sum_{j=1}^nz_j\right) \\ \end{pmatrix} \end{align}
このとき、\(y^{(2)}\)と標本分散には次のような関係が成り立つ。
\begin{align} {y^{(2)}}^\mathrm{T}y^{(2)} &= (PA_2z)^\mathrm{T}PA_2z \\ &= z^\mathrm{T}A_2^\mathrm{T}P^\mathrm{T}PA_2z \\ &= z^\mathrm{T}A_2^\mathrm{T}A_2z \\ &= z^\mathrm{T}A_2z \\ &= \frac{ns^2}{\sigma^2} \end{align}
各成分の独立性を確認する。
それぞれの成分の相関を、分散共分散行列で次のように調べる。
\begin{align} \mathrm{Cov}(y^{(k)},y^{(l)}) &= \mathbb{E}_z\left(y^{(k)}{y^{(l)}}^\mathrm{T}\right) \\ &= \mathbb{E}_z(PA_kz(PA_lz)^\mathrm{T}) \\ &= \mathbb{E}_z(PA_kzz^\mathrm{T}A_l^\mathrm{T}P^\mathrm{T}) \\ &= PA_k\mathbb{E}_z(zz^\mathrm{T})A_l^\mathrm{T}P^\mathrm{T} \\ \end{align}
ここで、\(\mathbb{E}_z(z_iz_j)=\delta_{i,j}\)であることから、
\begin{align} \mathbb{E}_z(zz^\mathrm{T}) = I \end{align}
なので、
\begin{align} \mathrm{Cov}(y^{(k)},y^{(l)}) &= PA_k\mathbb{E}_z(zz^\mathrm{T})A_l^\mathrm{T}P^\mathrm{T} \\ &= PA_kA_l^\mathrm{T}P^\mathrm{T} \\ &= PA_kP^\mathrm{T}PA_lP^\mathrm{T} \\ &= D_kD_l \\ \end{align}
となる。
\(k\neq l\)のときは、\(D_1D_2=0\)なので\(\mathrm{Cov}(y_k,y_l)=0\)。
\(k=l\)のときは、\(D_k\)が冪等であることから、
\begin{align} \mathrm{Cov}(y^{(k)},y^{(k)}) &= D_kD_k \\ &= D_k \\ \end{align}
したがって、n個の確率変数\(y := (y^{(1)}_1, y^{(2)}_2,y^{(2)}_3,\cdots,y^{(2)}_n)\)は独立であることがわかる。
なお、ここまでの議論は正規分布だけでなく一般の分布に対して成り立つ。
標本分散が従う分布
\(y\)は
\begin{align} y^{(1)}_1 &= \sqrt{n}\bar{z} \\ &\sim \sqrt{n}\mathcal{N}\left(0,\frac{1}{n}\right) \\ &= \mathcal{N}(0,1) \end{align}
\begin{align} y^{(2)}_i &= \frac{1}{\sqrt{i^2-i}}\left(-(i-1)z_i + \sum_{j=1}^{i-1}z_j\right) \\ &\sim \mathcal{N}\left(0,\frac{(i-1)^2}{i^2-i}\right) + \sum_{j=1}^{i-1}\mathcal{N}\left(0,\frac{1}{i^2-i}\right) \\ &= \mathcal{N}\left(0,\frac{(i-1)^2}{i^2-i} + \frac{i-1}{i^2-i}\right) \\ &= \mathcal{N}(0,1) \\ \end{align}
となることから、\(z\)と同じように各成分が標準正規分布に従っていることがわかる。
既に確認したことから、
\begin{align} \sum_{i=2}^ny_i^2 &= {y^{(2)}}^\mathrm{T}y^{(2)} \\ &= \frac{ns^2}{\sigma^2} \end{align}
となるので、標本分散が従う分布は「標準正規分布から取り出した\(n-1\)個の独立な値を2乗して足した値が従う分布」で表現できることがわかる。
そのような分布はχ²分布(カイ二乗分布)として定義されている。
標準正規分布\(\mathcal{N}(0,1)\)から取り出した\(k\)個の独立な値を\(\{z_i\}_{i=1}^k\)と表す。
このとき、\(\chi^2 := \sum_{i=1}^k z_i^2\)が従う分布を\(\chi^2_k\)と表し、χ²分布と呼ぶ。
χ²分布はその定義から再生性を持つことが直ちにわかる。
標本分散は\(y_i^2\)の\(n-1\)個の和で表されるので、
\begin{align} \frac{ns^2}{\sigma^2} \sim \chi^2_{n-1} \end{align}
と表されることになる。
χ²分布の確率密度関数
確率変数の変数変換
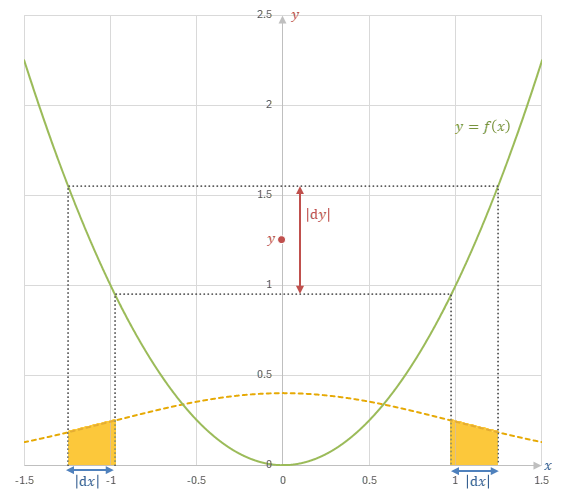
一般に、\(x\)が確率密度\(p_x(x)\)の分布に従っていて、滑らかな関数\(f\)によって\(y=f(x)\)と定義されるとき、\(y\)の分布に関して
\begin{align} p_y(y)|dy| = \sum_{x\in f^{-1}(y)}p_x(x)|dx| \end{align}
という関係が成り立つ必要がある。
したがって、\(y\)の分布は、
\begin{align} p_y(y) &= \sum_{x\in f^{-1}(y)}p_x(x)\left|\frac{dx}{dy}\right| \\ &= \sum_{x\in f^{-1}(y)}\frac{p_x(x)}{|f'(x)|} \\ \end{align}
と求めることができる。
確率変数\(x\)が確率密度関数\(p_x(x)\)で表される分布に従っているとする。
また、滑らかな関数\(f\)に対して\(y=f(x)\)として、\(y\)の確率密度関数を\(p_y(y)\)と表す。
このとき、
\begin{align} p_y(y)|dy| = \sum_{x\in f^{-1}(y)}p_x(x)|dx| \end{align}
という関係が成り立つ。
k=1の場合
\(k=1\)のχ²分布は、\(p_x=p_\mathcal{N}(\cdot|0,1), y=f(x)=x^2\)の場合の\(y\)の分布に等しい。
\(y<0\)のときは、\(f^{-1}(y)=\emptyset\)なので\(p_y(y)=0\)。
\(y>0\)のときは、\(f^{-1}(y)=\pm \sqrt{y}\)なので、
\begin{align} p_y(y) &= \sum_{x\in f^{-1}(y)}\frac{p_x(x)}{|f'(x)|} \\ &= \sum_{x\in \{-\sqrt{y},\sqrt{y}\}}\frac{p_\mathcal{N}(x|0,1)}{2|x|} \\ &= \frac{1}{2\sqrt{y}}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(-\sqrt{y})^2}{2}\right) + \frac{1}{2\sqrt{y}}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(\sqrt{y})^2}{2}\right) \\ &= \frac{1}{\sqrt{2\pi y}}\exp\left(-\frac{y}{2}\right) \\ \end{align}
つまり、\(\chi^2_1\)の確率密度は次のようになる。
\begin{align} p_{\chi^2}(x|1) &= \frac{1}{\sqrt{2\pi x}}\exp\left(-\frac{x}{2}\right) \qquad (x>0) \\ \end{align}
k=2の場合
\(k=2\)のχ²分布は、\(k=1\)のχ²分布の足し合わせによって求めることができる。
\(x>0\)に対して、
\begin{align} p_{\chi^2}(x|2) &= \int_{-\infty}^\infty p_{\chi^2}(z|1) p_{\chi^2}(x-z|1) dz \\ &= \int_0^x \frac{1}{\sqrt{2\pi z}}\exp\left(-\frac{z}{2}\right)\frac{1}{\sqrt{2\pi (x-z)}}\exp\left(-\frac{x-z}{2}\right) dz \\ &= \frac{1}{2\pi}\exp\left(-\frac{x}{2}\right)\int_0^x \frac{1}{\sqrt{z(x-z)}} dz \\ &= \frac{1}{2\pi}\exp\left(-\frac{x}{2}\right)\int_0^x \frac{2}{x}\frac{1}{\sqrt{1-\left(\frac{2z}{x}-1\right)^2}} dz \\ \end{align}
となるが、ここで\(\frac{2z}{x}-1 = \cos\theta\)となるように変数変換すると、
\begin{align} p_{\chi^2}(x|2) &= \frac{1}{2\pi}\exp\left(-\frac{x}{2}\right)\int_\pi^0 \frac{2}{x}\frac{1}{\sqrt{1-(\cos\theta)^2}} \frac{dz}{d\theta}d\theta \\ &= \frac{1}{2\pi}\exp\left(-\frac{x}{2}\right)\int_\pi^0 \frac{2}{x}\frac{1}{\sin\theta} \left(-\frac{x\sin\theta}{2}\right)d\theta \\ &= \frac{1}{2\pi}\exp\left(-\frac{x}{2}\right)\int_0^\pi d\theta \\ &= \frac{1}{2}\exp\left(-\frac{x}{2}\right) \end{align}
となり、\(\chi^2_2\)の確率密度が導出された。
\(k=2\)の場合は指数分布と一致することがわかる。
一般のkの場合
一般の\(k\)については、まず
\begin{align} p_{\chi^2}(x|k) = c_kx^{\frac{k}{2}-1}\exp\left(-\frac{x}{2}\right) \end{align}
が成り立つと仮定する。
この式は上で確かめたように\(k=1,2\)のときには成立し、\(c_1=1/\sqrt{2\pi}, c_2=1/2\)である。
このとき、
\begin{align} p_{\chi^2}(x|k+1) &= \int_{-\infty}^\infty p_{\chi^2}(x|k)p_{\chi^2}(x-z|1)dz \\ &= \int_{-\infty}^\infty c_kz^{\frac{k}{2}-1}\exp\left(-\frac{z}{2}\right) \frac{1}{\sqrt{2\pi (x-z)}}\exp\left(-\frac{x-z}{2}\right) dz \\ &= c_k\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x}{2}\right)\int_0^x z^{\frac{k}{2}-1}(x-z)^{-\frac{1}{2}} dz \\ \end{align}
となるが、\(y=z/x\)とするとベータ関数を用いて次のように表すことができる。
\begin{align} p_{\chi^2}(x|k+1) &= c_k\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x}{2}\right)\int_0^x z^{\frac{k}{2}-1}(x-z)^{-\frac{1}{2}} dz \\ &= c_k\frac{1}{\sqrt{2\pi}}x^{\frac{k}{2}-\frac{1}{2}}\exp\left(-\frac{x}{2}\right)\int_0^x \left(\frac{z}{x}\right)^{\frac{k}{2}-1}\left(1-\frac{z}{x}\right)^{-\frac{1}{2}} \frac{1}{x}dz \\ &= c_k\frac{1}{\sqrt{2\pi}}x^{\frac{k}{2}-\frac{1}{2}}\exp\left(-\frac{x}{2}\right)\int_0^1 y^{\frac{k}{2}-1}\left(1-y\right)^{-\frac{1}{2}}dy \\ &= c_k\frac{1}{\sqrt{2\pi}}x^{\frac{k+1}{2}-1}\exp\left(-\frac{x}{2}\right)\mathrm{B}\left(\frac{k}{2},\frac{1}{2}\right) \\ &= c_k\frac{1}{\sqrt{2\pi}}x^{\frac{k+1}{2}-1}\exp\left(-\frac{x}{2}\right)\frac{\mathrm{\Gamma}\left(\frac{k}{2}\right)\mathrm{\Gamma}\left(\frac{1}{2}\right)}{\mathrm{\Gamma}\left(\frac{k}{2}+\frac{1}{2}\right)} \\ &= c_k\frac{1}{\sqrt{2\pi}}x^{\frac{k+1}{2}-1}\exp\left(-\frac{x}{2}\right)\frac{\mathrm{\Gamma}\left(\frac{k}{2}\right)\sqrt{\pi}}{\mathrm{\Gamma}\left(\frac{k+1}{2}\right)} \\ &= c_k\frac{1}{\sqrt{2}}\frac{\mathrm{\Gamma}\left(\frac{k}{2}\right)}{\mathrm{\Gamma}\left(\frac{k+1}{2}\right)}x^{\frac{k+1}{2}-1}\exp\left(-\frac{x}{2}\right) \\ \end{align}
したがって、\(k+1\)の場合でも上記の仮定を満たすことがわかる。
このとき、
\begin{align} c_{k+1} = c_k\frac{1}{\sqrt{2}}\frac{\mathrm{\Gamma}\left(\frac{k}{2}\right)}{\mathrm{\Gamma}\left(\frac{k+1}{2}\right)} \end{align}
である。
これを変形すると、
\begin{align} c_{k+1}\mathrm{\Gamma}\left(\frac{k+1}{2}\right)2^{\frac{k+1}{2}} = c_k\mathrm{\Gamma}\left(\frac{k}{2}\right)2^{\frac{k}{2}} \end{align}
という関係が得られ、それらは全て
\begin{align} c_k\mathrm{\Gamma}\left(\frac{k}{2}\right)2^{\frac{k}{2}} &= c_2\mathrm{\Gamma}\left(\frac{2}{2}\right)2^{\frac{2}{2}} \\ &= \frac{1}{2}\mathrm{\Gamma}(1)2 \\ &= \mathrm{\Gamma}(1) \\ &= 1 \end{align}
になる。したがって係数\(c_k\)は、
\begin{align} c_k = \frac{1}{2^{\frac{k}{2}}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \end{align}
となるので、\(\chi^2_k\)の確率密度は
\begin{align} p_{\chi^2}(x|k) = \frac{x^{\frac{k}{2}-1}}{2^{\frac{k}{2}}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{x}{2}\right) \end{align}
となることがわかる。
χ²分布の確率密度関数は次のようになる。
\begin{align} p_{\chi^2}(x|k) = \frac{x^{\frac{k}{2}-1}}{2^{\frac{k}{2}}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{x}{2}\right) \end{align}
χ²分布の期待値はガンマ関数の定義から、
\begin{align} \int_0^\infty xp_{\chi^2}(x|k)dx &= \int_0^\infty \frac{x^{\frac{k}{2}}}{2^{\frac{k}{2}}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{x}{2}\right) dx \\ &= \frac{2}{\mathrm{\Gamma}\left(\frac{k}{2}\right)}\int_0^\infty \left(\frac{x}{2}\right)^{\frac{k}{2}} \exp\left(-\frac{x}{2}\right) d\frac{x}{2} \\ &= \frac{2}{\mathrm{\Gamma}\left(\frac{k}{2}\right)}\mathrm{\Gamma}\left(\frac{k}{2}+1\right) \\ &= \frac{2}{\mathrm{\Gamma}\left(\frac{k}{2}\right)}\frac{k}{2}\mathrm{\Gamma}\left(\frac{k}{2}\right) \\ &= k \end{align}
となる。
また、χ²分布の分散も同様に、
\begin{align} \int_0^\infty (x-k)^2p_{\chi^2}(x|k)dx &= - k^2 + \int_0^\infty x^2p_{\chi^2}(x|k)dx \\ &= - k^2 + \int_0^\infty \frac{x^{\frac{k}{2}+1}}{2^{\frac{k}{2}}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{x}{2}\right) dx \\ &= - k^2 + \frac{4}{\mathrm{\Gamma}\left(\frac{k}{2}\right)}\int_0^\infty \left(\frac{x}{2}\right)^{\frac{k}{2}+1} \exp\left(-\frac{x}{2}\right) d\frac{x}{2} \\ &= - k^2 + \frac{4}{\mathrm{\Gamma}\left(\frac{k}{2}\right)}\mathrm{\Gamma}\left(\frac{k}{2}+2\right) \\ &= - k^2 + \frac{4}{\mathrm{\Gamma}\left(\frac{k}{2}\right)}\left(\frac{k}{2}+1\right)\frac{k}{2}\mathrm{\Gamma}\left(\frac{k}{2}\right) \\ &= - k^2 + k(k+2) \\ &= 2k \end{align}
となる。
標本分散の確率密度
標本分散の話に戻ると、既に確かめた結果から
\begin{align} \frac{ns^2}{\sigma^2} \sim \chi^2_{n-1} \end{align}
が成り立つので、標本分散\(s^2\)の確率密度は
\begin{align} p(s^2) &= \frac{n}{\sigma^2}p_{\chi^2}\left(\frac{ns^2}{\sigma^2}\middle|n-1\right) \\ &= \frac{n}{\sigma^2}\frac{\left(\frac{ns^2}{\sigma^2}\right)^{\frac{k}{2}-1}}{2^{\frac{k}{2}}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{ns^2}{2\sigma^2}\right) \\ &= \left(\frac{n}{2\sigma^2}\right)^\frac{k}{2}\frac{\left(s^2\right)^{\frac{k}{2}-1}}{\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{ns^2}{2\sigma^2}\right) \\ \end{align}
と表すことができる。
また、\(\chi^2_k\)の期待値が\(k\)になるということは、
\begin{align} \frac{ns^2}{\sigma^2} \sim \chi^2_{n-1} \end{align}
の期待値が\(n-1\)になることを意味している。
つまり、「不偏分散\(\frac{n}{n-1}s^2\)の期待値が\(\sigma^2\)になる」という既に求めた結果と一致することが確かめられる。
標本の標準偏差
標本の標準偏差を\(s\)と表す。
\(s\)が従う分布はχ²分布の平方根であり、これはχ分布と呼ばれる。
\begin{align} \frac{\sqrt{n}s}{\sigma} &\sim \sqrt{\chi^2_{n-1}} \\ &=: \chi_{n-1} \end{align}
χ分布
\(y=\sqrt{x}\)とすると、χ分布の確率密度は次のようになる。
\begin{align} p_\chi(y|k) &= \frac{p_{\chi^2}(x|k)}{\frac{dy}{dx}} \\ &= \frac{p_{\chi^2}(x|k)}{\frac{1}{2\sqrt{x}}} \\ &= 2\sqrt{x}p_{\chi^2}(x|k) \\ &= 2yp_{\chi^2}(y^2|k) \\ &= 2y\frac{y^{k-2}}{2^{\frac{k}{2}}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{y^2}{2}\right) \\ &= \frac{y^{k-1}}{2^{\frac{k}{2}-1}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{y^2}{2}\right) \end{align}
この分布の平均は、
\begin{align} \int_0^\infty yp_\chi(y|k)dx &= \int_0^\infty y\frac{y^{k-1}}{2^{\frac{k}{2}-1}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{y^2}{2}\right) dy \\ &= \int_0^\infty x^{\frac{1}{2}}\frac{x^\frac{k-1}{2}}{2^{\frac{k}{2}-1}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{x}{2}\right) \frac{dy}{dx} dx \\ &= \int_0^\infty x^{\frac{1}{2}}\frac{x^\frac{k-1}{2}}{2^{\frac{k}{2}-1}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{x}{2}\right) \frac{1}{2\sqrt{x}} dx \\ &= \frac{1}{2^{\frac{k}{2}}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \int_0^\infty x^\frac{k-1}{2} \exp\left(-\frac{x}{2}\right) dx \\ &= \frac{\sqrt{2}}{\mathrm{\Gamma}\left(\frac{k}{2}\right)} \int_0^\infty \left(\frac{x}{2}\right)^\frac{k-1}{2} \exp\left(-\frac{x}{2}\right) d\frac{x}{2} \\ &= \sqrt{2}\frac{\mathrm{\Gamma}\left(\frac{k+1}{2}\right)}{\mathrm{\Gamma}\left(\frac{k}{2}\right)} \end{align}
となる。
同様に
\begin{align} \int_0^\infty y^2p_\chi(y|k)dx &= \int_0^\infty y^2\frac{y^{k-1}}{2^{\frac{k}{2}-1}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \exp\left(-\frac{y^2}{2}\right) dy \\ &= \frac{1}{2^{\frac{k}{2}}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \int_0^\infty x^\frac{1}{2}x^\frac{k-1}{2} \exp\left(-\frac{x}{2}\right) dx \\ &= \frac{1}{2^{\frac{k}{2}}\mathrm{\Gamma}\left(\frac{k}{2}\right)} \int_0^\infty x^\frac{k}{2} \exp\left(-\frac{x}{2}\right) dx \\ &= \frac{2}{\mathrm{\Gamma}\left(\frac{k}{2}\right)} \int_0^\infty \left(\frac{x}{2}\right)^\frac{k}{2} \exp\left(-\frac{x}{2}\right) d\frac{x}{2} \\ &= \frac{2\mathrm{\Gamma}\left(\frac{k}{2}+1\right)}{\mathrm{\Gamma}\left(\frac{k}{2}\right)} \\ &= 2\cdot\frac{k}{2} \\ &= k \end{align}
となることから、分散は
\begin{align} k-2\frac{\mathrm{\Gamma}\left(\frac{k+1}{2}\right)^2}{\mathrm{\Gamma}\left(\frac{k}{2}\right)^2} \end{align}
となる。
標本の標準偏差の平均と分散
したがって、標本の標準偏差の平均は、
\begin{align} \sqrt{\frac{2}{n}}\frac{\mathrm{\Gamma}\left(\frac{n}{2}\right)}{\mathrm{\Gamma}\left(\frac{n-1}{2}\right)}\sigma \end{align}
となる。
このことから、
\begin{align} \sqrt{\frac{\mathrm{\Gamma}\left(\frac{n-1}{2}\right)}{2\mathrm{\Gamma}\left(\frac{n}{2}\right)}\sum_{k=1}^n(x_k-\bar{x})^2} \end{align}
と計算した値が、標準偏差の不偏推定量になると言える。(不偏分散の平方根は標準偏差の不偏推定量にはならない)
また、標本の標準偏差の分散は、
\begin{align} \left(\frac{n-1}{n}-\frac{2}{n}\frac{\mathrm{\Gamma}\left(\frac{n}{2}\right)^2}{\mathrm{\Gamma}\left(\frac{n-1}{2}\right)^2}\right)\sigma^2 \end{align}
となる。