有限体
本稿では符号理論の基礎概念である有限体について解説する。
関連ページ
- 有限体 (本ページ)
- 誤り訂正符号 - BCH符号・RS符号
- QRコードの仕組み
- QRコード生成ツール
目次
有限体の構成方法
体の定義
体(可換体, field)とは、加算・乗算とそれぞれの逆演算(=減算・除算)が定義され、更に分配法則が成り立つような代数的構造(=集合と演算)。
- 加算 (\(+\))
- 交換法則が成り立つ: \(a+b=b+a\)
- 結合法則が成り立つ: \((a+b)+c=a+(b+c)\)
- 単位元\(0\)が存在: \(a+0=a\)
- 逆元\(-a\)が存在: \(a+(-a)=0\)
- したがって減算を定義可能: \(a-b=a+(-b)\)
- 乗算 (\(\times\))
- 交換法則が成り立つ: \(a\times b=b\times a\)
- 結合法則が成り立つ: \((a\times b)\times c=a\times(b\times c)\)
- 単位元\(1\)が存在: \(a\times1=a\)
- 0以外に対して逆元\(a^{-1}\)が存在: \(a\times a^{-1}=1\)
- したがって除算を定義可能: \(\frac{a}{b}=a\times b^{-1}\)
- 分配法則が成り立つ: \(a\times(b+c)=a\times b+a\times c\)
特に要素数が有限である体を有限体(Finite field, Galois field)と言う。また、有限体の要素数を位数と言う。
素数位数の有限体
位数が素数の有限体を具体的に構成してみよう。
\(p\)を任意の素数とする。
集合\(\mathbb{F}_p:=\{0, 1, 2, \cdots , p-1\}\)に対して\(p\)を法とした加算・乗算を定義する。つまり、\(\mathbb{F}_p\)の加算・乗算の結果は、通常の自然数の加算・乗算の結果を\(p\)で割った余りとなる。
例えば\(p=7\)のとき
\begin{array}{rlcll} 4+5 &=& 9 &=& 2 \\ 4\cdot5 &=& 20 &=& 6 \end{array}
というようになる。
このように構成した集合と演算が体の性質を満たすかどうか確認する。
- 交換法則・結合法則・単位元・分配法則については自然数で成立することから\(\mathbb{F}_p\)でも成立。
- 加法の逆元は、\(-a=p-a\in\mathbb{F}_p\)が存在する。
- 乗法の逆元についてはFermatの小定理より\(a\neq0\)に対して\(a^{p-1}=1\)となることから、\(a^{-1}=a^{p-2}\)が存在する。
素数\(p\)と、\(0<a<p\)を満たす整数\(a\)に対して次の式が成り立つ。
\begin{align} a^{p-1} \equiv 1 \pmod p \end{align}
\(a^p\equiv a\)の証明
まず\(0^p=0\)が成り立つ。
\(a^p\equiv a\)が成り立つとき、二項定理によって\((a+1)^p\)を展開すると、
\begin{align} (a+1)^p &= a^p + \sum_{k=1}^{p-1}\frac{p!}{(p-k)!k!}a^k + 1 \\ &\equiv a + \sum_{k=1}^{p-1}\frac{p!}{(p-k)!k!}a^k + 1 \end{align}
となる。
二項係数\(\frac{p!}{(p-k)!k!}\)は常に整数。また\(1\leq k\leq p-1\)のとき、分子は\(p\)を因数に持つ一方で、分母は\(p\)を因数に含まない。したがって、二項係数は\(p\)で割り切れる。よって、
\begin{align} (a+1)^p &\equiv a + \sum_{k=1}^{p-1}\frac{p!}{(p-k)!k!}a^k + 1 \\ &\equiv a + 0 + 1 \\ &= a + 1 \\ \end{align}
が成り立つ。
したがって帰納的に全ての\(a\geq0\)に対して\(a^p\equiv a\)が成り立つ。
\(a^{p-1}\equiv1\)の証明
これはつまり、\(a^p = a+np\)となる整数\(n\)が存在するということなので、
\begin{align} a(a^{p-1}-1) = np \end{align}
となる。
左辺は\(a\)を因数に持つが、右辺は\(a\)と\(p\)が互いに素なので\(n\)が\(a\)の倍数になっていなければならない。したがって、\(a\neq0\)のとき\(m:=\frac{n}{a}\)は整数。
\begin{align} a^{p-1}-1 = mp \end{align}
となることから、\(a^{p-1}\equiv1\)が成り立つ。
したがって\(\mathbb{F}_p\)は体の性質を全て満たし、有限体であることがわかる。
(位数\(p\)の有限体を\(\mathrm{GF}(p)\)と表す場合もある)
Fermatの小定理を用いる必要があるので、同様の方法では位数が素数以外の有限体を構成することはできない。
素数冪位数の有限体
別の方法で位数が素数の冪乗\(p^m\)の有限体を構成することもできる。
多項式環
\(\mathbb{F}_p\)係数の多項式の集合(=多項式環)を\(\mathbb{F}_p[x]\)と表す。
つまり、
\begin{align} \mathbb{F}_p[x] = \left\{a_mx^m+a_{m-1}x^{m-1}+\cdots+a_1x+a_0 \middle| m\geq0, a_k\in\mathbb{F}_p\right\} \end{align}
とする。
この集合には多項式としての加算・乗算を定義することができる。(多項式の係数は\(\mathbb{F}_p\)上で演算する)
例えば\(\mathbb{F}_7[x]\)の場合、加算・乗算は
\begin{align} (2x^2+5) + (5x^2+2x+3) &= (2+5)x^2+(0+2)x+(5+3) \\ &= 7x^2+2x+8 \\ &= 0x^2+2x+1 \\ &= 2x+1 \\ \end{align}
\begin{align} (2x^2+5)(5x^2+2x+3) &= 10x^4 + (4+0)x^3 + (6+0+25)x^2 + (10+0)x + 15 \\ &= 10x^4 + 4x^3 + 31x^2 + 10x + 15 \\ &= 3x^4 + 4x^3 + 3x^2 + 3x + 1 \\ \end{align}
となる。
これらの演算の本質は、有限個の\(\mathbb{F}_p\)の要素からなる組(=多項式の係数)同士に定義された演算でしかなく、\(x\)はあくまで形式的な表記であってその実体を考える必要はない。言い換えれば、単に視認しやすいように多項式のような表記で表しているに過ぎない。
このような多項式は形式的冪級数と呼ばれる。
Galois拡大
\(m\)次多項式\(f(x)\in\mathbb{F}_p[x]\)を取り、\(\mathbb{F}_p[x]\)の\(m-1\)次以下の多項式全体による部分集合に\(f(x)\)を法とした加算・乗算を定義したものを、\(\mathbb{F}_p[x]/(f(x))\)と表す。
つまり、\(\mathbb{F}_p[x]/(f(x))\)の加算・乗算の結果は、\(\mathbb{F}_p[x]\)上の加算・乗算の結果を\(f(x)\)で割った余りとなる。
例えば\(\mathbb{F}_7[x]/(x^3+5x^2+3)\)の場合の乗算は、
\begin{align} (2x^2+5)(5x^2+2x+3) &= 3x^4 + 4x^3 + 3x^2 + 3x + 1 \\ &= (3x+3)(x^3+5x^2+3)+2x^2+x+6 \\ &= 2x^2+x+6 \\ \end{align}
となる。(加算については\(2\)次多項式内で閉じているので余りを計算する必要はない)
このように定義された代数的構造はGalois拡大と呼ばれる。
\(\mathbb{F}_p[x]/(f(x))\)には\(\mathbb{F}_p\)係数の全ての\(m-1\)次多項式が含まれるので、要素数(=位数)は\(p^m\)、つまり素数冪となる。
\(\mathbb{F}_p[x]/(f(x))\)が有限体になるかどうか確認する。
- 交換法則・結合法則・単位元・分配法則については多項式同士・係数\(\mathbb{F}_p\)同士の演算でそれぞれ成立することから\(\mathbb{F}_p[x]/(f(x))\)でも成立。
- 加法の逆元は、多項式の各係数を\(p\)から引いた
\(-(a_nx^n+\cdots+a_1x+a_0)=(p-a_n)x^n+\cdots+(p-a_1)x+p-a_0\in\mathbb{F}_p[x]/(f(x))\)
が存在する。
ここまでの性質(体の性質から乗法の逆元の存在を除いたもの)を満たす代数的構造は可換環と呼ばれる。
可換環\(\mathbb{F}_p[x]/(f(x))\)に乗法の逆元を導入するためには、\(f(x)\)が一定の条件を満たさなければならない。\(\mathbb{F}_p[x]/(f(x))\)が有限体になる条件と、有限体の性質を以下にまとめて紹介する。
要素数\(q\)の可換環\(F\)に対して次は全て同値。(ここまでは素数位数の有限体についても成立)
- \(F\)が有限体 (つまり除算を定義できる)
- 原始元\(\alpha\in F\backslash\{0\}\)が存在して、かつ\(\alpha^{q-1}=1\)
(原始元とは任意の\(a\in F\backslash\{0\}\)に対して非負の整数\(n_a\)を用いて\(a=\alpha^{n_a}\)と表せるような\(\alpha\)のこと) - 任意の\(a\in F\backslash\{0\}\)に対して\(a^{q-1}=1\)
- 任意の\(a\in F\backslash\{0\}\)に対して\(a^{n_a}=1\)となるような整数\(n_a\geq1\)が存在
(そのような最小の\(n_a\)を\(a\)の位数と言う。このとき、\(a^n\)は\(n\)を1ずつ増やしていくと\(n_a\)周期で同じ値を繰り返すことになる。有限体の要素数を表す「位数」と同じ言葉だが別の概念なので注意)
更に位数\(q\)の有限体\(\mathbb{F}_q\)に対して\(F=\mathbb{F}_q[x]/(f(x))\)としたとき、次も同値。
(\(f(x)\)の次数を\(m\)とすると、\(q=p^m\))
- \(f(x)\)は既約多項式
(既約多項式とは、1次以上\(m-1\)次以下の多項式\(g(x),h(x)\)の積によって\(f(x)=g(x)h(x)\)と表すことが不可能な1次以上の多項式\(f(x)\)のこと)
なお既約多項式\(f(x)\)に関して、\(y(x):=x\)が\(\mathbb{F}_q[x]/(f(x))\)の原始元になるとき、\(f(x)\)は原始多項式であると言う。
下図のように証明していく。
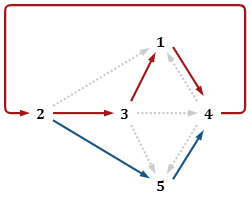
証明の流れ (点線の方向にも容易に証明することができる)
2⇒3
任意の\(a\in F\)に対して\(a^{q-1}=\left(\alpha^{n_a}\right)^{q-1}=\left(\alpha^{q-1}\right)^{n_a}=1^{n_a}=1\)が成り立つ。
3⇒1
\(a^{-1}:=a^{q-2}\)とすれば、\(a\cdot a^{-1}=a\cdot a^{q-2}=a^{q-1}=1\)が成り立つ。
1⇒4
\(F\)の要素数が有限であることから、\(a^n\)の\(n\)を0から増やしていくとどこかで同じ値が出現しそれ以降ループする。(\(a^n=0\)でループする場合も含めて良い)
つまり、\(a^n=a^m\)となるような\(0\leq m<n\)が共に存在する。このとき、\(a^{n-m}=a^n/a^m=a^m/a^m=1\)なので、4の条件を満たす\(n_a=n-m \geq 1\)が存在すると言える。
4⇒2
\(a\in F\backslash\{0\}\)を任意に取り、\(a\)の位数を\(n_a\)とする。
\(a^m=a^n\)となるような\(m<n<n_a\)が存在すると仮定すると、\(n_a\)より小さい\(n_a-(n-m)>0\)に対して
\begin{align} 1 &= a^{n_a} \\ &= a^{n_a-n}a^n \\ &= a^{n_a-n}a^m \\ &= a^{n_a-(n-m)} \\ \end{align}
となり、位数\(n_a\)の最小性に矛盾する。
よって\(0\leq n<n_a\)において\(a^n\)は全て異なる値を取る。つまり、\(\{a^n|0\leq n\} = \{a^n|0\leq n<n_a\}\)の要素数は\(n_a\)である。
3⇒1の証明と同様に、4⇒1も成立する。したがって\(F\)は(有限)体。
後述の補題1より、体\(F\)において\(y^{n_a}-1=0\)となるような\(y\in F\)は高々\(n_a\)個しか存在しない。
一方、\(\{a^n|0\leq n\}\)の\(n_a\)個の要素は全て\(y^{n_a}=1\)を満たす。
したがって集合の大きさが一致するので、\(\{a^n|0\leq n\}=\{y|y^{n_a}=1\}\)となる。
\(\{a^n|0\leq n\} = F\backslash\{0\}\)のときは\(a\)が原始元となるので直ちに2が成立。
\(\{a^n|0\leq n\} \neq F\backslash\{0\}\)のときを考える。
\(b\in F\backslash\left(\{0\}\cup\{a^n|0\leq n\}\right)\)を取り、その位数を\(n_b\)とする。
\(\{a^n|0\leq n\}=\{y|y^{n_a}=1\}\)なので、\(b^{n_a}\neq1\)が成立する。ここで\(n_b\)が\(n_a\)を割り切ると仮定すると、\(b^{n_a}=\left(b^{n_b}\right)^{n_a/n_b}=1^{n_a/n_b}=1\)となって矛盾するので、\(n_b\)は\(n_a\)を割り切らないことがわかる。
\(n_a\)と\(n_b\)が互いに素のとき、\(c:=ab\)としてその位数を\(n_c\)とする。
- \(c^{n_an_b}=\left(a^{n_a}\right)^{n_b}\left(b^{n_b}\right)^{n_a}=1^{n_b}1^{n_a}=1\cdot1=1\)なので、\(n_an_b\)は\(n_c\)で割り切れる。
- \(a^{n_bn_c}=a^{n_bn_c}b^{n_bn_c}=(ab)^{n_cn_b}=1^{n_b}=1\)なので、\(n_bn_c\)は\(n_a\)で割り切れる。\(n_a\)と\(n_b\)は互いに素なので、\(n_c\)は\(n_a\)で割り切れる。
同様に\(n_c\)は\(n_b\)で割り切れる。
これらより、\(n_c=n_an_b\)となり、\(n_a\)より位数の大きい要素\(c=ab\)が存在することがわかる。
\(n_a\)と\(n_b\)が互いに素ではないとき、\(n_a\)と\(n_b\)をそれぞれ素因数分解して\(n_a=\prod_ip_i^{a_i}, n_b=\prod_ip_i^{b_i}\)とする。
また、これらを用いて新たに\(n_a':=\prod_{a_i\geq b_i}p_i^{a_i}, n_b'=\prod_{a_i<b_i}p_i^{b_i}\)という自然数を定義する。\(n_a'\)は\(n_a\)を、\(n_b'\)は\(n_b\)を割り切る。また、\(n_a'\)と\(n_b'\)は互いに素。
\(a\)の位数は\(n_a\)なので、\(a':=a^{n_a/n_a'}\)の位数は\(n_a'\)である。同様に\(b':=a^{n_b/n_b'}\)の位数は\(n_b'\)である。
したがって\(n_a\)と\(n_b\)が互いに素のときと同様に、\(c:=a'b'\)の位数は\(n_c:=n_a'n_b'\)となる。\(n_c\)は\(n_a\)と\(n_b\)の最小公倍数で、更に\(n_b\)は\(n_a\)を割り切らないので、\(n_c>n_a\)となる。
よっていずれの場合も\(n_a\)より大きい位数の要素\(c\)を新たに得ることができる。
\(c\)を改めて\(a\)と置けば、\(\{a^n|0\leq n\}\neq F\backslash\{0\}\)となる限りこの手順を繰り返すことができ、位数は増大し続ける。位数には上限があるので、最終的に\(\{a^n|0\leq n\}=F\backslash\{0\}\)となるような\(a\)が得られることで手順の繰り返しが止まる。このようにして得られた最終的な\(a\)は\(F\)の原始元となる。
また、\(\{a^n|0\leq n\}=F\backslash\{0\}\)のそれぞれの要素数を取ると、\(n_a=q-1\)となり原始元の位数が\(q-1\)であることもわかる。
2⇒5
まず、常に\(\alpha^n\neq0\)となることを示す。
原始元の性質より、\(F\backslash\{0\}\subset\{\alpha^n|0\leq n\}\)。また\(q-1\leq n\)のとき\(\alpha^n=\alpha^{n-(q-1)}\alpha^{q-1}=\alpha^{n-(q-1)}\)なので、\(\{\alpha^n|0\leq n\}=\{\alpha^n|0\leq n\leq q-2\}\)という包含関係が成り立つ。したがって、\(F\backslash\{0\}\subset\{\alpha^n|0\leq n\leq q-2\}\)となるが、左右の要素の個数はどちらも\(q-1\)なので集合は一致する。
よって常に\(\alpha^n\neq0\)となる。
¬5を仮定する。つまり、1次以上\(m-1\)次以下の多項式\(g(x), h(x)\)を用いて\(f(x)=g(x)h(x)\)と表される。(このことを「\(f(x)\)は可約である」と言う)
\(g,h\)は\(F\backslash\{0\}\)の要素でもあるので、2の条件から\(g=\alpha^{n_g}, h=\alpha^{n_h}\)と表すことができる。\(F=F_q[x]/(f(x))\)上の演算は\(f(x)\)で割った余りが結果になるので、\(\alpha^{n_g+n_h} = \alpha^{n_g}\alpha^{n_h} = gh = f = 0\)となるが、これは最初に示した\(\alpha^n\neq0\)という事実に矛盾する。
したがって、¬5の仮定が正しくなかったことがわかる。
5⇒4
1⇒4の証明と同様に¬4を仮定すると、ある\(a\in F\backslash\{0\}\)に対して、\(a^m=a^n\)かつ\(a^{m-1}\neq a^{n-1}\)となるような\(1\leq m<n\)が存在する。
したがって、
\begin{align} 0 &\equiv a^n-a^m \pmod {f(x)} \\ &= a\left(a^{n-1}-a^{m-1}\right)\\ \end{align}
となる。
\(f(x)\)は既約なので、\(f\)と\(a^{n-1}-a^{m-1}\)の最小公倍数は\(1\)となる。したがって、後述の補題2より
\begin{align} 1 = sf + t(a^{n-1}-a^{m-1}) \end{align}
となるような多項式\(s, t\)が存在する。両辺に\(a\)を掛けると、
\begin{align} a &= saf + ta(a^{n-1}-a^{m-1}) \\ &\equiv sa\times 0 + t\times0 \pmod {f(x)} \\ &= 0 \end{align}
となり、\(a\in F\backslash\{0\}\)と選んだことと矛盾する。よって、¬4の仮定が正しくなかったことがわかる。
体\(F\)値の\(n\)次多項式\(f(y)\)について、根(=\(f(y)=0\)を満たす解\(y\))の個数は高々\(n\)個。
\(f(y)=0\)に\(n+1\)個の異なる解\(\{y_k\}_{k=0}^n\)が存在すると仮定する。
\(f_n(y):=f(y)\)とする。このとき、\(f_n(y\))は\(n\)次多項式であり、\(\{y_k\}_{k=0}^n\)は\(f_n(y)\)の根となる。
\(f_n(y)\)を\(y-y_n\)で割ると、\(n-1\)次多項式\(f_{n-1}(y)\)と定数\(h\)によって
\begin{align} f_n(y) = f_{n-1}(y)(y-y_n) + h \end{align}
と表すことができる。ここで、\(y\)に\(y_n\)を代入すると\(0=f_n(y_n)=0+h=h\)となるので、
\begin{align} f_n(y) = f_{n-1}(y)(y-y_n) \end{align}
となる。
\(\{y_k\}_{k=0}^n\)は互いに異なる値なので、任意の\(0\leq k\leq n-1\)に対して\(y_k-y_n\neq0\)が成り立つ。したがって、上の式に\(y=y_k\)を代入して両辺を\(y-y_n\)で割ることで
\begin{align} f_{n-1}(y_k) &= \frac{f_n(y_k)}{y_k-y_n} \\ &= \frac{0}{y_k-y_n} \\ &= 0 \end{align}
となり、\(\{y_k\}_{k=0}^{n-1}\)は\(n-1\)次方程式\(f_{n-1}(y)\)の根になることがわかる。
これを繰り返すことで、0次多項式(つまり定数)\(f_0(y)=a\neq0\)を用いて
\begin{align} f(y) &= f_n(y) \\ &= f_{n-1}(y)(y-y_n) \\ &\:\; \vdots \\ &= f_0(y)(y-y_n)(y-y_{n-1})\cdots(y-y_1) \\ &= a(y-y_n)(y-y_{n-1})\cdots(y-y_1) \\ \end{align}
と表すことができる。
\(y=y_0\)を代入すると、
\begin{align} 0 &= f(y_0) \\ &= a(y_0-y_n)(y_0-y_{n-1})\cdots(y_0-y_1) \\ \end{align}
となり、更に両辺を\((y_0-y_n)(y_0-y_{n-1})\cdots(y_0-y_1)\)で割ると\(a=0\)となって矛盾。
したがって\(f(y)=0\)に\(n+1\)個の異なる解\(\{y_k\}_{k=0}^n\)が存在するという仮定が間違っていたことがわかる。
有限体\(F_q\)と既約多項式\(f(x)\)に対して\(F=F_q[x]/(f(x))\)とする。
多項式\(a, b\in F\)を取り、\(a, b\)の最大公約数(=\(a,b\)を共に割り切る最大次数の多項式)を\(c\)とする。このとき、
\begin{align} sa+tb=c \end{align}
を満たす多項式\(s, t\in F\)が存在する。
公約数を求める
\(a, b\)の内、次数が大きい方を\(r_0\)、次数が小さい方を\(r_1\)とする。
\(r_0\)を\(r_1\)で割ると、次の関係を満たすように\(r_1\)より低次数の多項式\(r_2\)を取ることができる。
(ただし\(r_1\)が0以外の定数のときは\(r_2=0\))
\begin{align} r_0 = q_2r_1 + r_2 \end{align}
\(r_2\neq 0\)のとき、\(r_1\)を\(r_2\)で割ると、次の関係を満たすように\(r_2\)より低次数の多項式\(r_3\)を取ることができる。
(ただし\(r_2\)が0以外の定数のときは\(r_3=0\))
\begin{align} r_1 = q_3r_2 + r_3 \end{align}
これを繰り返すことで\(r_k\)の次数は減少し続け、いつか\(r_{n+1}=0\)となるような\(n\)に行き着く。(このような手法をEuclidの互除法と言う)
\begin{align} r_0 &= q_2r_1 + r_2 \\ r_1 &= q_3r_2 + r_3 \\ r_2 &= q_4r_3 + r_4 \\ &\:\;\vdots \\ r_{n-3} &= q_{n-1}r_{n-2} + r_{n-1} \\ r_{n-2} &= q_nr_{n-1} + r_n \\ r_{n-1} &= q_{n+1}r_n + r_{n+1} \\ &= q_{n+1}r_n \end{align}
これは、\(r_n\)が\(r_{n-1}\)を割り切ることを意味する。
また、一つ前の式に遡ると、
\begin{align} r_{n-2} &= q_nr_{n-1} + r_n \\ &= q_nq_{n+1}r_n + r_n \\ &= (q_nq_{n+1} + 1)r_n \\ \end{align}
となるので、\(r_{n-2}\)も\(r_n\)で割り切れることがわかる。
これを繰り返すことで、全ての\(r_k\)は\(r_n\)で割り切れることがわかる。したがって、\(r_n\)は\(a,b\)の公約数となる。
目的の式を構築する
再びEuclidの互除法の式を下から見てみよう。
\(s_n=1, s_{n-1}=-q_n\)とすると、\(r_{n-2} = q_nr_{n-1} + r_n\)という式は次のように表すこともできる。
\begin{align} s_nr_{n-2} &= -s_{n-1}r_{n-1} + r_n \end{align}
また、
\begin{align} r_{n-3} &= q_{n-1}r_{n-2} + r_{n-1} \\ s_nr_{n-2} &= -s_{n-1}r_{n-1} + r_n \end{align}
から\(r_{n-1}\)を消去すると、
\begin{align} s_{n-1}r_{n-3} &= -(s_n-s_{n-1}q_{n-1})r_{n-2} + r_n \\ &=: -s_{n-2}r_{n-2} + r_n \end{align}
と表すことができる。(ただし、\(s_{n-2}:=s_n-s_{n-1}q_{n-1}\)とした)
これを繰り返すことで、
\begin{align} s_2r_0 &= -s_1r_1 + r_n \end{align}
となるような\(s_2, s_1\)が存在することがわかる。\(s:=s_2, t:=s_1, c:=r_n\)とすることで、
\begin{align} sa + tb = c \end{align}
となる。
\(c\)が最大公約数であることを示す
\(a,b\)の公約数\(d\)を任意に取る。つまり、\(a=q_ad, b=q_bd\)となるような\(q_a, q_b\)が存在する。
このとき、
\begin{align} c &= sa + tb \\ &= (sq_a + tq_b)d \end{align}
となって、\(d\)は\(c\)を割り切る。
よって、どんな\(d\)に対しても\(c\)の次数は\(d\)の次数以上になるので、\(c\)は最大公約数である。
したがって、\(f(x)\)が\(\mathbb{F}_p[x]\)上の既約多項式ならば、\(F=\mathbb{F}_p[x]/(f(x))\)は有限体となる。
このときの\(F\)の位数は\(p^m\)なので、\(\mathbb{F}_p[x]/(f(x)) = \mathbb{F}_{p^m}\)と表す。(あるいは\(\mathrm{GF}(p^m)\)と表す)
素数冪以外の位数の有限体
素数冪以外、つまり複数の異なる素数の合成数となるような位数の有限体は存在しない。
有限体\(F\)に対して素数\(p\)と自然数\(n\)が存在して、\(F\)の位数は\(p^n\)となる。
標数の基本的な性質
\(u\in F\)を\(s\)回足す演算を\(s\#u\)と表す。このとき
\begin{align} (s+t)\#u &= s\#u + t\#u \\ s\#(u+v) &= s\#u + s\#v \\ (st)\#u &= s\#(t\#u) \\ 1\#u &= u \end{align}
が成り立つ。(これは線形空間のスカラー倍が満たすべき要件である)
また、\(F\)は有限体なので
\begin{align} (s\#u)\cdot(t\#v)=(st)\#(u\cdot v) \end{align}
という関係も成り立つ。(\(\cdot\)は\(F\)で定義された乗算)
\(F\)の要素数は有限なので、\(1\in F\)に対して\(s\#1=0\)となるような正の整数\(s\)が存在する。そのような最小の\(s\)を\(F\)の標数と言う。
\(s\)が\(F\)の標数であるとき、1以外の任意の\(u\in F\backslash\{0,1\}\)に対しても、
\begin{align} s\#u &= s\#(1\cdot u) \\ &= (s\#1)\cdot u \\ &= 0\cdot u \\ &= 0 \\ \end{align}
が成り立つ。
また逆に、\(t<s\)に対して\(t\#u=0\)となると仮定すると、
\begin{align} 0 &= 0\cdot u^{-1} \\ &= (t\#u)\cdot u^{-1} \\ &= (t\#1)\cdot u\cdot u^{-1} \\ &= t\#1 \\ \end{align}
となって\(s\)の最小性に矛盾する。
したがって、標数\(s\)は任意の\(u\in F\backslash\{0\}\)に対しても\(s\#u=0\)となる最小の自然数であると言える。
\(F\)の標数は素数
標数\(s\)が合成数\(s=ab\)であると仮定すると、
\begin{align} 0 &= (ab)\#1 \\ &= (ab)\#(1\cdot1) \\ &= (a\#1)\cdot(b\#1) \end{align}
となるが、\(s\)の最小性より\(a\#1\)も\(b\#1\)も0とはならないので上の式は矛盾している。
したがって\(s\)は素数あるいは1である。(ただし標数1の体は要素が\(\{0\}\)しかない自明な体となり、考察する意味がほとんどないのでここでは\(s\)は素数とする)
\(F\)の位数は素数冪
\(s\)は素数なので、\(\mathbb{F}_s=\{0, 1, 2, \cdots, s-1\}\)は有限体である。
\(F\)の\(\mathbb{F}_s\)上のスカラー倍を上記の\(\#\)演算によって定めると、\(F\)は線形空間の要件を満たす。
\(F\)は有限の線形空間なので有限個の基底\(\{e_i\}_{i=1}^n\)が存在し、それぞれの基底の係数は\(\mathbb{F}_s\)値なので\(s\)個の値を取る。
したがって、\(F\)の位数は\(s^n\)となり、これは素数冪である。(\(n=1\)のときは素数)
例
素数位数の有限体
\(p=2, 3, 5, 7, 11, 13\)のときの\(\mathbb{F}_p\)の例を見てみよう。
p=2
\(p=2\)の場合\(\mathbb{F}_p=\{0, 1\}\)であり、演算は次のように定めれば良い。
\begin{align} 0 + 0 &= 0 \\ 0 + 1 &= 1 \\ 1 + 1 &= 0 \end{align}
\begin{align} 0 - 0 &= 0 \\ 0 - 1 &= 1 \\ 1 - 0 &= 1 \\ 1 - 1 &= 0 \end{align}
\begin{align} 0 \times 0 &= 0 \\ 0 \times 1 &= 0 \\ 1 \times 1 &= 1 \end{align}
\begin{align} 0 / 1 &= 0 \\ 1 / 1 &= 1 \end{align}
式を見ると減算と加算は結果が全く同じになっているので、\(\mathbb{F}_2\)では\(a-b=a+b\)と置き換えて良いことがわかる。加算と減算はXOR演算と捉えることもできる。
\(\mathbb{F}_p\backslash\{0\}=\{1\}\)なので、原始元は\(\alpha=1\)。
p=3
\(p=3\)の場合\(\mathbb{F}_p=\{0, 1, 2\}\)である。各要素の冪乗を下の表に示す。
原始元は\(\alpha=2\)。(表内の黄色の行)
| \(a^0\) | \(a^1\) | \(a^2\) |
|---|---|---|
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 1 | 2 | 1 |
p=5
原始元は\(\alpha=2,3\)。
| \(a^0\) | \(a^1\) | \(a^2\) | \(a^3\) | \(a^4\) |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 4 | 3 | 1 |
| 1 | 3 | 4 | 2 | 1 |
| 1 | 4 | 1 | 4 | 1 |
p=7
原始元は\(\alpha=3,5\)。
| \(a^0\) | \(a^1\) | \(a^2\) | \(a^3\) | \(a^4\) | \(a^5\) | \(a^6\) |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 4 | 1 | 2 | 4 | 1 |
| 1 | 3 | 2 | 6 | 4 | 5 | 1 |
| 1 | 4 | 2 | 1 | 4 | 2 | 1 |
| 1 | 5 | 4 | 6 | 2 | 3 | 1 |
| 1 | 6 | 1 | 6 | 1 | 6 | 1 |
p=11
原始元は\(\alpha=2,6,7,8\)。
| \(a^0\) | \(a^1\) | \(a^2\) | \(a^3\) | \(a^4\) | \(a^5\) | \(a^6\) | \(a^7\) | \(a^8\) | \(a^9\) | \(a^{10}\) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 4 | 8 | 5 | 10 | 9 | 7 | 3 | 6 | 1 |
| 1 | 3 | 9 | 5 | 4 | 1 | 3 | 9 | 5 | 4 | 1 |
| 1 | 4 | 5 | 9 | 3 | 1 | 4 | 5 | 9 | 3 | 1 |
| 1 | 5 | 3 | 4 | 9 | 1 | 5 | 3 | 4 | 9 | 1 |
| 1 | 6 | 3 | 7 | 9 | 10 | 5 | 8 | 4 | 2 | 1 |
| 1 | 7 | 5 | 2 | 3 | 10 | 4 | 6 | 9 | 8 | 1 |
| 1 | 8 | 9 | 6 | 4 | 10 | 3 | 2 | 5 | 7 | 1 |
| 1 | 9 | 4 | 3 | 5 | 1 | 9 | 4 | 3 | 5 | 1 |
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | 1 |
p=13
原始元は\(\alpha=2,6,7,11\)。
| \(a^0\) | \(a^1\) | \(a^2\) | \(a^3\) | \(a^4\) | \(a^5\) | \(a^6\) | \(a^7\) | \(a^8\) | \(a^9\) | \(a^{10}\) | \(a^{11}\) | \(a^{12}\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 4 | 8 | 3 | 6 | 12 | 11 | 9 | 5 | 10 | 7 | 1 |
| 1 | 3 | 9 | 1 | 3 | 9 | 1 | 3 | 9 | 1 | 3 | 9 | 1 |
| 1 | 4 | 3 | 12 | 9 | 10 | 1 | 4 | 3 | 12 | 9 | 10 | 1 |
| 1 | 5 | 12 | 8 | 1 | 5 | 12 | 8 | 1 | 5 | 12 | 8 | 1 |
| 1 | 6 | 10 | 8 | 9 | 2 | 12 | 7 | 3 | 5 | 4 | 11 | 1 |
| 1 | 7 | 10 | 5 | 9 | 11 | 12 | 6 | 3 | 8 | 4 | 2 | 1 |
| 1 | 8 | 12 | 5 | 1 | 8 | 12 | 5 | 1 | 8 | 12 | 5 | 1 |
| 1 | 9 | 3 | 1 | 9 | 3 | 1 | 9 | 3 | 1 | 9 | 3 | 1 |
| 1 | 10 | 9 | 12 | 3 | 4 | 1 | 10 | 9 | 12 | 3 | 4 | 1 |
| 1 | 11 | 4 | 5 | 3 | 7 | 12 | 2 | 9 | 8 | 10 | 6 | 1 |
| 1 | 12 | 1 | 12 | 1 | 12 | 1 | 12 | 1 | 12 | 1 | 12 | 1 |
素数冪位数の有限体
既約多項式
\(\mathbb{F}_{p^m}\)の例を見る前に、まずは既約多項式について調べる。
ある多項式が既約であるかどうかは、より低次の既知の既約多項式全てで割ってみることで判定することができる。
\(\mathbb{F}_2[x]\)の11次までの既約多項式を次の表に掲載する。
表内では係数を並べることで多項式を表現する。例えば\(x^4+x^3+1\)は\(x^4, x^3, x^2, x, 1\)の係数がそれぞれ\(1,1,0,0,1\)なので2進表記は11001となる。
既約多項式の中で更に原始多項式となるものは黄色の背景で表す。
| 次数 | 既約多項式 |
|---|---|
| 1 | 10 |
| 11 | |
| 2 | 111 |
| 3 | 1011 |
| 1101 | |
| 4 | 10011 |
| 11001 | |
| 11111 | |
| 5 | 100101 |
| 101001 | |
| 101111 | |
| 110111 | |
| 111011 | |
| 111101 | |
| 6 | 1000011 |
| 1001001 | |
| 1010111 | |
| 1011011 | |
| 1100001 | |
| 1100111 | |
| 1101101 | |
| 1110011 | |
| 1110101 | |
| 7 | 10000011 |
| 10001001 | |
| 10001111 | |
| 10010001 | |
| 10011101 | |
| 10100111 | |
| 10101011 | |
| 10111001 | |
| 10111111 | |
| 11000001 | |
| 11001011 | |
| 11010011 | |
| 11010101 | |
| 11100101 | |
| 11101111 | |
| 11110001 | |
| 11110111 | |
| 11111101 | |
| 8 | 100011011 |
| 100011101 | |
| 100101011 | |
| 100101101 | |
| 100111001 | |
| 100111111 | |
| 101001101 | |
| 101011111 | |
| 101100011 | |
| 101100101 | |
| 101101001 | |
| 101110001 | |
| 101110111 | |
| 101111011 | |
| 110000111 | |
| 110001011 | |
| 110001101 | |
| 110011111 | |
| 110100011 | |
| 110101001 | |
| 110110001 | |
| 110111101 | |
| 111000011 | |
| 111001111 | |
| 111010111 | |
| 111011101 | |
| 111100111 | |
| 111110011 | |
| 111110101 | |
| 111111001 | |
| 9 | 1000000011 |
| 1000010001 | |
| 1000010111 | |
| 1000011011 | |
| 1000100001 | |
| 1000101101 | |
| 1000110011 | |
| 1001001011 | |
| 1001011001 | |
| 1001011111 | |
| 1001100101 | |
| 1001101001 | |
| 1001101111 | |
| 1001110111 | |
| 1001111101 | |
| 1010000111 | |
| 1010010101 | |
| 1010011001 | |
| 1010100011 | |
| 1010100101 | |
| 1010101111 | |
| 1010110111 | |
| 1010111101 | |
| 1011001111 | |
| 1011010001 | |
| 1011011011 | |
| 1011110101 | |
| 1011111001 | |
| 1100000001 | |
| 1100010011 | |
| 1100010101 | |
| 1100011111 | |
| 1100100011 | |
| 1100110001 | |
| 1100111011 | |
| 1101001001 | |
| 1101001111 | |
| 1101011011 | |
| 1101100001 | |
| 1101101011 | |
| 1101101101 | |
| 1101110011 | |
| 1101111111 | |
| 1110000101 | |
| 1110001111 | |
| 1110100001 | |
| 1110110101 | |
| 1110111001 | |
| 1111000111 | |
| 1111001011 | |
| 1111001101 | |
| 1111010101 | |
| 1111011001 | |
| 1111100011 | |
| 1111101001 | |
| 1111111011 | |
| 10 | 10000001001 |
| 10000001111 | |
| 10000011011 | |
| 10000011101 | |
| 10000100111 | |
| 10000101101 | |
| 10000110101 | |
| 10001000111 | |
| 10001010011 | |
| 10001100011 | |
| 10001100101 | |
| 10001101111 | |
| 10010000001 | |
| 10010001011 | |
| 10010011001 | |
| 10010101001 | |
| 10010101111 | |
| 10011000101 | |
| 10011001001 | |
| 10011010111 | |
| 10011100111 | |
| 10011101101 | |
| 10011110011 | |
| 10011111111 | |
| 10100001011 | |
| 10100001101 | |
| 10100011001 | |
| 10100011111 | |
| 10100100011 | |
| 10100110001 | |
| 10100111101 | |
| 10101000011 | |
| 10101010111 | |
| 10101100001 | |
| 10101100111 | |
| 10101101011 | |
| 10110000101 | |
| 10110001111 | |
| 10110010111 | |
| 10110011011 | |
| 10110100001 | |
| 10110101011 | |
| 10110111001 | |
| 10111000001 | |
| 10111000111 | |
| 10111100101 | |
| 10111110111 | |
| 10111111011 | |
| 11000010011 | |
| 11000010101 | |
| 11000100011 | |
| 11000100101 | |
| 11000110001 | |
| 11000110111 | |
| 11001000011 | |
| 11001001111 | |
| 11001010001 | |
| 11001011011 | |
| 11001111001 | |
| 11001111111 | |
| 11010000101 | |
| 11010001001 | |
| 11010100111 | |
| 11010101101 | |
| 11010110101 | |
| 11010111111 | |
| 11011000001 | |
| 11011001101 | |
| 11011010011 | |
| 11011011111 | |
| 11011110111 | |
| 11011111101 | |
| 11100001111 | |
| 11100010001 | |
| 11100010111 | |
| 11100011101 | |
| 11100100001 | |
| 11100101011 | |
| 11100110101 | |
| 11100111001 | |
| 11101000111 | |
| 11101001101 | |
| 11101010101 | |
| 11101011001 | |
| 11101100011 | |
| 11101111011 | |
| 11101111101 | |
| 11110000001 | |
| 11110000111 | |
| 11110001101 | |
| 11110010011 | |
| 11110101001 | |
| 11110110001 | |
| 11111000101 | |
| 11111011011 | |
| 11111101011 | |
| 11111110011 | |
| 11111111001 | |
| 11111111111 | |
| 11 | 100000000101 |
| 100000010111 | |
| 100000101011 | |
| 100000101101 | |
| 100001000111 | |
| 100001100011 | |
| 100001100101 | |
| 100001110001 | |
| 100001111011 | |
| 100010001101 | |
| 100010010101 | |
| 100010011111 | |
| 100010101001 | |
| 100010110001 | |
| 100011000011 | |
| 100011001111 | |
| 100011010001 | |
| 100011100001 | |
| 100011100111 | |
| 100011101011 | |
| 100011110101 | |
| 100100001101 | |
| 100100010011 | |
| 100100100101 | |
| 100100101001 | |
| 100100110111 | |
| 100100111011 | |
| 100100111101 | |
| 100101000101 | |
| 100101001001 | |
| 100101010001 | |
| 100101011011 | |
| 100101110011 | |
| 100101110101 | |
| 100101111111 | |
| 100110000011 | |
| 100110001111 | |
| 100110101011 | |
| 100110101101 | |
| 100110111001 | |
| 100111000111 | |
| 100111011001 | |
| 100111100101 | |
| 100111101111 | |
| 100111110111 | |
| 101000000001 | |
| 101000000111 | |
| 101000010011 | |
| 101000010101 | |
| 101000101001 | |
| 101001001001 | |
| 101001100001 | |
| 101001101101 | |
| 101001111001 | |
| 101001111111 | |
| 101010000101 | |
| 101010010001 | |
| 101010011101 | |
| 101010100111 | |
| 101010101011 | |
| 101010110011 | |
| 101010110101 | |
| 101011010101 | |
| 101011011111 | |
| 101011100011 | |
| 101011101001 | |
| 101011101111 | |
| 101011110001 | |
| 101011111011 | |
| 101100000011 | |
| 101100001001 | |
| 101100010001 | |
| 101100110011 | |
| 101100111111 | |
| 101101000001 | |
| 101101001011 | |
| 101101011001 | |
| 101101011111 | |
| 101101100101 | |
| 101101101111 | |
| 101101111101 | |
| 101110000111 | |
| 101110001011 | |
| 101110010011 | |
| 101110010101 | |
| 101110101111 | |
| 101110110111 | |
| 101110111101 | |
| 101111001001 | |
| 101111011011 | |
| 101111011101 | |
| 101111100111 | |
| 101111101101 | |
| 110000001011 | |
| 110000001101 | |
| 110000011001 | |
| 110000011111 | |
| 110000110001 | |
| 110001010111 | |
| 110001100001 | |
| 110001101011 | |
| 110001110011 | |
| 110001110101 | |
| 110010000101 | |
| 110010001001 | |
| 110010010111 | |
| 110010011011 | |
| 110010011101 | |
| 110010110011 | |
| 110010111111 | |
| 110011000111 | |
| 110011001101 | |
| 110011010011 | |
| 110011010101 | |
| 110011100011 | |
| 110011101001 | |
| 110011110111 | |
| 110100000011 | |
| 110100001111 | |
| 110100011101 | |
| 110100100111 | |
| 110100101101 | |
| 110101000001 | |
| 110101000111 | |
| 110101010101 | |
| 110101011001 | |
| 110101100011 | |
| 110101101111 | |
| 110101110001 | |
| 110110010011 | |
| 110110011111 | |
| 110110101001 | |
| 110110111011 | |
| 110110111101 | |
| 110111001001 | |
| 110111010111 | |
| 110111011011 | |
| 110111100001 | |
| 110111100111 | |
| 110111110101 | |
| 110111111111 | |
| 111000000101 | |
| 111000011101 | |
| 111000100001 | |
| 111000100111 | |
| 111000101011 | |
| 111000110011 | |
| 111000111001 | |
| 111001000111 | |
| 111001001011 | |
| 111001010101 | |
| 111001011111 | |
| 111001110001 | |
| 111001111011 | |
| 111001111101 | |
| 111010000001 | |
| 111010010011 | |
| 111010011111 | |
| 111010100011 | |
| 111010111011 | |
| 111011001001 | |
| 111011001111 | |
| 111011011101 | |
| 111011110011 | |
| 111011111001 | |
| 111100001011 | |
| 111100011001 | |
| 111100110001 | |
| 111100110111 | |
| 111101011101 | |
| 111101101011 | |
| 111101101101 | |
| 111101110101 | |
| 111101111001 | |
| 111110000011 | |
| 111110010001 | |
| 111110010111 | |
| 111110011011 | |
| 111110100111 | |
| 111110101101 | |
| 111110110101 | |
| 111111001101 | |
| 111111010011 | |
| 111111100101 | |
| 111111101001 | |
| 111111111011 |
(この表を作るために使ったJSコードはこちら)
\(f(x)=x^8+x^4+x^3+x^2+1\)
8次の既約多項式\(f(x)=x^8+x^4+x^3+x^2+1\)(2進表記で100011101)を選び、\(\mathbb{F}_{2^8}=\mathbb{F}_2[x]/(f(x))\)とした場合の例を見てみよう。
下の表で確かめられるように、この例では\(y = \alpha(x) := x = \) 00000010が原始元となる。
全ての\(y\in\mathbb{F}_{2^8}\)は8桁の2進数で表記することができるが、その値を10進数に変換することで0から255までの値と対応付けることができる。
| \(y\) | \(y^{-1}\) | ||||
|---|---|---|---|---|---|
| 10進表記 | 2進表記 | 冪乗表記 | 10進表記 | 2進表記 | 冪乗表記 |
| 0 | 00000000 | ||||
| 1 | 00000001 | \(\alpha^{0}\) | 1 | 00000001 | \(\alpha^{0}\) |
| 2 | 00000010 | \(\alpha^{1}\) | 142 | 10001110 | \(\alpha^{254}\) |
| 3 | 00000011 | \(\alpha^{25}\) | 244 | 11110100 | \(\alpha^{230}\) |
| 4 | 00000100 | \(\alpha^{2}\) | 71 | 01000111 | \(\alpha^{253}\) |
| 5 | 00000101 | \(\alpha^{50}\) | 167 | 10100111 | \(\alpha^{205}\) |
| 6 | 00000110 | \(\alpha^{26}\) | 122 | 01111010 | \(\alpha^{229}\) |
| 7 | 00000111 | \(\alpha^{198}\) | 186 | 10111010 | \(\alpha^{57}\) |
| 8 | 00001000 | \(\alpha^{3}\) | 173 | 10101101 | \(\alpha^{252}\) |
| 9 | 00001001 | \(\alpha^{223}\) | 157 | 10011101 | \(\alpha^{32}\) |
| 10 | 00001010 | \(\alpha^{51}\) | 221 | 11011101 | \(\alpha^{204}\) |
| 11 | 00001011 | \(\alpha^{238}\) | 152 | 10011000 | \(\alpha^{17}\) |
| 12 | 00001100 | \(\alpha^{27}\) | 61 | 00111101 | \(\alpha^{228}\) |
| 13 | 00001101 | \(\alpha^{104}\) | 170 | 10101010 | \(\alpha^{151}\) |
| 14 | 00001110 | \(\alpha^{199}\) | 93 | 01011101 | \(\alpha^{56}\) |
| 15 | 00001111 | \(\alpha^{75}\) | 150 | 10010110 | \(\alpha^{180}\) |
| 16 | 00010000 | \(\alpha^{4}\) | 216 | 11011000 | \(\alpha^{251}\) |
| 17 | 00010001 | \(\alpha^{100}\) | 114 | 01110010 | \(\alpha^{155}\) |
| 18 | 00010010 | \(\alpha^{224}\) | 192 | 11000000 | \(\alpha^{31}\) |
| 19 | 00010011 | \(\alpha^{14}\) | 88 | 01011000 | \(\alpha^{241}\) |
| 20 | 00010100 | \(\alpha^{52}\) | 224 | 11100000 | \(\alpha^{203}\) |
| 21 | 00010101 | \(\alpha^{141}\) | 62 | 00111110 | \(\alpha^{114}\) |
| 22 | 00010110 | \(\alpha^{239}\) | 76 | 01001100 | \(\alpha^{16}\) |
| 23 | 00010111 | \(\alpha^{129}\) | 102 | 01100110 | \(\alpha^{126}\) |
| 24 | 00011000 | \(\alpha^{28}\) | 144 | 10010000 | \(\alpha^{227}\) |
| 25 | 00011001 | \(\alpha^{193}\) | 222 | 11011110 | \(\alpha^{62}\) |
| 26 | 00011010 | \(\alpha^{105}\) | 85 | 01010101 | \(\alpha^{150}\) |
| 27 | 00011011 | \(\alpha^{248}\) | 128 | 10000000 | \(\alpha^{7}\) |
| 28 | 00011100 | \(\alpha^{200}\) | 160 | 10100000 | \(\alpha^{55}\) |
| 29 | 00011101 | \(\alpha^{8}\) | 131 | 10000011 | \(\alpha^{247}\) |
| 30 | 00011110 | \(\alpha^{76}\) | 75 | 01001011 | \(\alpha^{179}\) |
| 31 | 00011111 | \(\alpha^{113}\) | 42 | 00101010 | \(\alpha^{142}\) |
| 32 | 00100000 | \(\alpha^{5}\) | 108 | 01101100 | \(\alpha^{250}\) |
| 33 | 00100001 | \(\alpha^{138}\) | 237 | 11101101 | \(\alpha^{117}\) |
| 34 | 00100010 | \(\alpha^{101}\) | 57 | 00111001 | \(\alpha^{154}\) |
| 35 | 00100011 | \(\alpha^{47}\) | 81 | 01010001 | \(\alpha^{208}\) |
| 36 | 00100100 | \(\alpha^{225}\) | 96 | 01100000 | \(\alpha^{30}\) |
| 37 | 00100101 | \(\alpha^{36}\) | 86 | 01010110 | \(\alpha^{219}\) |
| 38 | 00100110 | \(\alpha^{15}\) | 44 | 00101100 | \(\alpha^{240}\) |
| 39 | 00100111 | \(\alpha^{33}\) | 138 | 10001010 | \(\alpha^{222}\) |
| 40 | 00101000 | \(\alpha^{53}\) | 112 | 01110000 | \(\alpha^{202}\) |
| 41 | 00101001 | \(\alpha^{147}\) | 208 | 11010000 | \(\alpha^{108}\) |
| 42 | 00101010 | \(\alpha^{142}\) | 31 | 00011111 | \(\alpha^{113}\) |
| 43 | 00101011 | \(\alpha^{218}\) | 74 | 01001010 | \(\alpha^{37}\) |
| 44 | 00101100 | \(\alpha^{240}\) | 38 | 00100110 | \(\alpha^{15}\) |
| 45 | 00101101 | \(\alpha^{18}\) | 139 | 10001011 | \(\alpha^{237}\) |
| 46 | 00101110 | \(\alpha^{130}\) | 51 | 00110011 | \(\alpha^{125}\) |
| 47 | 00101111 | \(\alpha^{69}\) | 110 | 01101110 | \(\alpha^{186}\) |
| 48 | 00110000 | \(\alpha^{29}\) | 72 | 01001000 | \(\alpha^{226}\) |
| 49 | 00110001 | \(\alpha^{181}\) | 137 | 10001001 | \(\alpha^{74}\) |
| 50 | 00110010 | \(\alpha^{194}\) | 111 | 01101111 | \(\alpha^{61}\) |
| 51 | 00110011 | \(\alpha^{125}\) | 46 | 00101110 | \(\alpha^{130}\) |
| 52 | 00110100 | \(\alpha^{106}\) | 164 | 10100100 | \(\alpha^{149}\) |
| 53 | 00110101 | \(\alpha^{39}\) | 195 | 11000011 | \(\alpha^{216}\) |
| 54 | 00110110 | \(\alpha^{249}\) | 64 | 01000000 | \(\alpha^{6}\) |
| 55 | 00110111 | \(\alpha^{185}\) | 94 | 01011110 | \(\alpha^{70}\) |
| 56 | 00111000 | \(\alpha^{201}\) | 80 | 01010000 | \(\alpha^{54}\) |
| 57 | 00111001 | \(\alpha^{154}\) | 34 | 00100010 | \(\alpha^{101}\) |
| 58 | 00111010 | \(\alpha^{9}\) | 207 | 11001111 | \(\alpha^{246}\) |
| 59 | 00111011 | \(\alpha^{120}\) | 169 | 10101001 | \(\alpha^{135}\) |
| 60 | 00111100 | \(\alpha^{77}\) | 171 | 10101011 | \(\alpha^{178}\) |
| 61 | 00111101 | \(\alpha^{228}\) | 12 | 00001100 | \(\alpha^{27}\) |
| 62 | 00111110 | \(\alpha^{114}\) | 21 | 00010101 | \(\alpha^{141}\) |
| 63 | 00111111 | \(\alpha^{166}\) | 225 | 11100001 | \(\alpha^{89}\) |
| 64 | 01000000 | \(\alpha^{6}\) | 54 | 00110110 | \(\alpha^{249}\) |
| 65 | 01000001 | \(\alpha^{191}\) | 95 | 01011111 | \(\alpha^{64}\) |
| 66 | 01000010 | \(\alpha^{139}\) | 248 | 11111000 | \(\alpha^{116}\) |
| 67 | 01000011 | \(\alpha^{98}\) | 213 | 11010101 | \(\alpha^{157}\) |
| 68 | 01000100 | \(\alpha^{102}\) | 146 | 10010010 | \(\alpha^{153}\) |
| 69 | 01000101 | \(\alpha^{221}\) | 78 | 01001110 | \(\alpha^{34}\) |
| 70 | 01000110 | \(\alpha^{48}\) | 166 | 10100110 | \(\alpha^{207}\) |
| 71 | 01000111 | \(\alpha^{253}\) | 4 | 00000100 | \(\alpha^{2}\) |
| 72 | 01001000 | \(\alpha^{226}\) | 48 | 00110000 | \(\alpha^{29}\) |
| 73 | 01001001 | \(\alpha^{152}\) | 136 | 10001000 | \(\alpha^{103}\) |
| 74 | 01001010 | \(\alpha^{37}\) | 43 | 00101011 | \(\alpha^{218}\) |
| 75 | 01001011 | \(\alpha^{179}\) | 30 | 00011110 | \(\alpha^{76}\) |
| 76 | 01001100 | \(\alpha^{16}\) | 22 | 00010110 | \(\alpha^{239}\) |
| 77 | 01001101 | \(\alpha^{145}\) | 103 | 01100111 | \(\alpha^{110}\) |
| 78 | 01001110 | \(\alpha^{34}\) | 69 | 01000101 | \(\alpha^{221}\) |
| 79 | 01001111 | \(\alpha^{136}\) | 147 | 10010011 | \(\alpha^{119}\) |
| 80 | 01010000 | \(\alpha^{54}\) | 56 | 00111000 | \(\alpha^{201}\) |
| 81 | 01010001 | \(\alpha^{208}\) | 35 | 00100011 | \(\alpha^{47}\) |
| 82 | 01010010 | \(\alpha^{148}\) | 104 | 01101000 | \(\alpha^{107}\) |
| 83 | 01010011 | \(\alpha^{206}\) | 140 | 10001100 | \(\alpha^{49}\) |
| 84 | 01010100 | \(\alpha^{143}\) | 129 | 10000001 | \(\alpha^{112}\) |
| 85 | 01010101 | \(\alpha^{150}\) | 26 | 00011010 | \(\alpha^{105}\) |
| 86 | 01010110 | \(\alpha^{219}\) | 37 | 00100101 | \(\alpha^{36}\) |
| 87 | 01010111 | \(\alpha^{189}\) | 97 | 01100001 | \(\alpha^{66}\) |
| 88 | 01011000 | \(\alpha^{241}\) | 19 | 00010011 | \(\alpha^{14}\) |
| 89 | 01011001 | \(\alpha^{210}\) | 193 | 11000001 | \(\alpha^{45}\) |
| 90 | 01011010 | \(\alpha^{19}\) | 203 | 11001011 | \(\alpha^{236}\) |
| 91 | 01011011 | \(\alpha^{92}\) | 99 | 01100011 | \(\alpha^{163}\) |
| 92 | 01011100 | \(\alpha^{131}\) | 151 | 10010111 | \(\alpha^{124}\) |
| 93 | 01011101 | \(\alpha^{56}\) | 14 | 00001110 | \(\alpha^{199}\) |
| 94 | 01011110 | \(\alpha^{70}\) | 55 | 00110111 | \(\alpha^{185}\) |
| 95 | 01011111 | \(\alpha^{64}\) | 65 | 01000001 | \(\alpha^{191}\) |
| 96 | 01100000 | \(\alpha^{30}\) | 36 | 00100100 | \(\alpha^{225}\) |
| 97 | 01100001 | \(\alpha^{66}\) | 87 | 01010111 | \(\alpha^{189}\) |
| 98 | 01100010 | \(\alpha^{182}\) | 202 | 11001010 | \(\alpha^{73}\) |
| 99 | 01100011 | \(\alpha^{163}\) | 91 | 01011011 | \(\alpha^{92}\) |
| 100 | 01100100 | \(\alpha^{195}\) | 185 | 10111001 | \(\alpha^{60}\) |
| 101 | 01100101 | \(\alpha^{72}\) | 196 | 11000100 | \(\alpha^{183}\) |
| 102 | 01100110 | \(\alpha^{126}\) | 23 | 00010111 | \(\alpha^{129}\) |
| 103 | 01100111 | \(\alpha^{110}\) | 77 | 01001101 | \(\alpha^{145}\) |
| 104 | 01101000 | \(\alpha^{107}\) | 82 | 01010010 | \(\alpha^{148}\) |
| 105 | 01101001 | \(\alpha^{58}\) | 141 | 10001101 | \(\alpha^{197}\) |
| 106 | 01101010 | \(\alpha^{40}\) | 239 | 11101111 | \(\alpha^{215}\) |
| 107 | 01101011 | \(\alpha^{84}\) | 179 | 10110011 | \(\alpha^{171}\) |
| 108 | 01101100 | \(\alpha^{250}\) | 32 | 00100000 | \(\alpha^{5}\) |
| 109 | 01101101 | \(\alpha^{133}\) | 236 | 11101100 | \(\alpha^{122}\) |
| 110 | 01101110 | \(\alpha^{186}\) | 47 | 00101111 | \(\alpha^{69}\) |
| 111 | 01101111 | \(\alpha^{61}\) | 50 | 00110010 | \(\alpha^{194}\) |
| 112 | 01110000 | \(\alpha^{202}\) | 40 | 00101000 | \(\alpha^{53}\) |
| 113 | 01110001 | \(\alpha^{94}\) | 209 | 11010001 | \(\alpha^{161}\) |
| 114 | 01110010 | \(\alpha^{155}\) | 17 | 00010001 | \(\alpha^{100}\) |
| 115 | 01110011 | \(\alpha^{159}\) | 217 | 11011001 | \(\alpha^{96}\) |
| 116 | 01110100 | \(\alpha^{10}\) | 233 | 11101001 | \(\alpha^{245}\) |
| 117 | 01110101 | \(\alpha^{21}\) | 251 | 11111011 | \(\alpha^{234}\) |
| 118 | 01110110 | \(\alpha^{121}\) | 218 | 11011010 | \(\alpha^{134}\) |
| 119 | 01110111 | \(\alpha^{43}\) | 121 | 01111001 | \(\alpha^{212}\) |
| 120 | 01111000 | \(\alpha^{78}\) | 219 | 11011011 | \(\alpha^{177}\) |
| 121 | 01111001 | \(\alpha^{212}\) | 119 | 01110111 | \(\alpha^{43}\) |
| 122 | 01111010 | \(\alpha^{229}\) | 6 | 00000110 | \(\alpha^{26}\) |
| 123 | 01111011 | \(\alpha^{172}\) | 187 | 10111011 | \(\alpha^{83}\) |
| 124 | 01111100 | \(\alpha^{115}\) | 132 | 10000100 | \(\alpha^{140}\) |
| 125 | 01111101 | \(\alpha^{243}\) | 205 | 11001101 | \(\alpha^{12}\) |
| 126 | 01111110 | \(\alpha^{167}\) | 254 | 11111110 | \(\alpha^{88}\) |
| 127 | 01111111 | \(\alpha^{87}\) | 252 | 11111100 | \(\alpha^{168}\) |
| 128 | 10000000 | \(\alpha^{7}\) | 27 | 00011011 | \(\alpha^{248}\) |
| 129 | 10000001 | \(\alpha^{112}\) | 84 | 01010100 | \(\alpha^{143}\) |
| 130 | 10000010 | \(\alpha^{192}\) | 161 | 10100001 | \(\alpha^{63}\) |
| 131 | 10000011 | \(\alpha^{247}\) | 29 | 00011101 | \(\alpha^{8}\) |
| 132 | 10000100 | \(\alpha^{140}\) | 124 | 01111100 | \(\alpha^{115}\) |
| 133 | 10000101 | \(\alpha^{128}\) | 204 | 11001100 | \(\alpha^{127}\) |
| 134 | 10000110 | \(\alpha^{99}\) | 228 | 11100100 | \(\alpha^{156}\) |
| 135 | 10000111 | \(\alpha^{13}\) | 176 | 10110000 | \(\alpha^{242}\) |
| 136 | 10001000 | \(\alpha^{103}\) | 73 | 01001001 | \(\alpha^{152}\) |
| 137 | 10001001 | \(\alpha^{74}\) | 49 | 00110001 | \(\alpha^{181}\) |
| 138 | 10001010 | \(\alpha^{222}\) | 39 | 00100111 | \(\alpha^{33}\) |
| 139 | 10001011 | \(\alpha^{237}\) | 45 | 00101101 | \(\alpha^{18}\) |
| 140 | 10001100 | \(\alpha^{49}\) | 83 | 01010011 | \(\alpha^{206}\) |
| 141 | 10001101 | \(\alpha^{197}\) | 105 | 01101001 | \(\alpha^{58}\) |
| 142 | 10001110 | \(\alpha^{254}\) | 2 | 00000010 | \(\alpha^{1}\) |
| 143 | 10001111 | \(\alpha^{24}\) | 245 | 11110101 | \(\alpha^{231}\) |
| 144 | 10010000 | \(\alpha^{227}\) | 24 | 00011000 | \(\alpha^{28}\) |
| 145 | 10010001 | \(\alpha^{165}\) | 223 | 11011111 | \(\alpha^{90}\) |
| 146 | 10010010 | \(\alpha^{153}\) | 68 | 01000100 | \(\alpha^{102}\) |
| 147 | 10010011 | \(\alpha^{119}\) | 79 | 01001111 | \(\alpha^{136}\) |
| 148 | 10010100 | \(\alpha^{38}\) | 155 | 10011011 | \(\alpha^{217}\) |
| 149 | 10010101 | \(\alpha^{184}\) | 188 | 10111100 | \(\alpha^{71}\) |
| 150 | 10010110 | \(\alpha^{180}\) | 15 | 00001111 | \(\alpha^{75}\) |
| 151 | 10010111 | \(\alpha^{124}\) | 92 | 01011100 | \(\alpha^{131}\) |
| 152 | 10011000 | \(\alpha^{17}\) | 11 | 00001011 | \(\alpha^{238}\) |
| 153 | 10011001 | \(\alpha^{68}\) | 220 | 11011100 | \(\alpha^{187}\) |
| 154 | 10011010 | \(\alpha^{146}\) | 189 | 10111101 | \(\alpha^{109}\) |
| 155 | 10011011 | \(\alpha^{217}\) | 148 | 10010100 | \(\alpha^{38}\) |
| 156 | 10011100 | \(\alpha^{35}\) | 172 | 10101100 | \(\alpha^{220}\) |
| 157 | 10011101 | \(\alpha^{32}\) | 9 | 00001001 | \(\alpha^{223}\) |
| 158 | 10011110 | \(\alpha^{137}\) | 199 | 11000111 | \(\alpha^{118}\) |
| 159 | 10011111 | \(\alpha^{46}\) | 162 | 10100010 | \(\alpha^{209}\) |
| 160 | 10100000 | \(\alpha^{55}\) | 28 | 00011100 | \(\alpha^{200}\) |
| 161 | 10100001 | \(\alpha^{63}\) | 130 | 10000010 | \(\alpha^{192}\) |
| 162 | 10100010 | \(\alpha^{209}\) | 159 | 10011111 | \(\alpha^{46}\) |
| 163 | 10100011 | \(\alpha^{91}\) | 198 | 11000110 | \(\alpha^{164}\) |
| 164 | 10100100 | \(\alpha^{149}\) | 52 | 00110100 | \(\alpha^{106}\) |
| 165 | 10100101 | \(\alpha^{188}\) | 194 | 11000010 | \(\alpha^{67}\) |
| 166 | 10100110 | \(\alpha^{207}\) | 70 | 01000110 | \(\alpha^{48}\) |
| 167 | 10100111 | \(\alpha^{205}\) | 5 | 00000101 | \(\alpha^{50}\) |
| 168 | 10101000 | \(\alpha^{144}\) | 206 | 11001110 | \(\alpha^{111}\) |
| 169 | 10101001 | \(\alpha^{135}\) | 59 | 00111011 | \(\alpha^{120}\) |
| 170 | 10101010 | \(\alpha^{151}\) | 13 | 00001101 | \(\alpha^{104}\) |
| 171 | 10101011 | \(\alpha^{178}\) | 60 | 00111100 | \(\alpha^{77}\) |
| 172 | 10101100 | \(\alpha^{220}\) | 156 | 10011100 | \(\alpha^{35}\) |
| 173 | 10101101 | \(\alpha^{252}\) | 8 | 00001000 | \(\alpha^{3}\) |
| 174 | 10101110 | \(\alpha^{190}\) | 190 | 10111110 | \(\alpha^{65}\) |
| 175 | 10101111 | \(\alpha^{97}\) | 183 | 10110111 | \(\alpha^{158}\) |
| 176 | 10110000 | \(\alpha^{242}\) | 135 | 10000111 | \(\alpha^{13}\) |
| 177 | 10110001 | \(\alpha^{86}\) | 229 | 11100101 | \(\alpha^{169}\) |
| 178 | 10110010 | \(\alpha^{211}\) | 238 | 11101110 | \(\alpha^{44}\) |
| 179 | 10110011 | \(\alpha^{171}\) | 107 | 01101011 | \(\alpha^{84}\) |
| 180 | 10110100 | \(\alpha^{20}\) | 235 | 11101011 | \(\alpha^{235}\) |
| 181 | 10110101 | \(\alpha^{42}\) | 242 | 11110010 | \(\alpha^{213}\) |
| 182 | 10110110 | \(\alpha^{93}\) | 191 | 10111111 | \(\alpha^{162}\) |
| 183 | 10110111 | \(\alpha^{158}\) | 175 | 10101111 | \(\alpha^{97}\) |
| 184 | 10111000 | \(\alpha^{132}\) | 197 | 11000101 | \(\alpha^{123}\) |
| 185 | 10111001 | \(\alpha^{60}\) | 100 | 01100100 | \(\alpha^{195}\) |
| 186 | 10111010 | \(\alpha^{57}\) | 7 | 00000111 | \(\alpha^{198}\) |
| 187 | 10111011 | \(\alpha^{83}\) | 123 | 01111011 | \(\alpha^{172}\) |
| 188 | 10111100 | \(\alpha^{71}\) | 149 | 10010101 | \(\alpha^{184}\) |
| 189 | 10111101 | \(\alpha^{109}\) | 154 | 10011010 | \(\alpha^{146}\) |
| 190 | 10111110 | \(\alpha^{65}\) | 174 | 10101110 | \(\alpha^{190}\) |
| 191 | 10111111 | \(\alpha^{162}\) | 182 | 10110110 | \(\alpha^{93}\) |
| 192 | 11000000 | \(\alpha^{31}\) | 18 | 00010010 | \(\alpha^{224}\) |
| 193 | 11000001 | \(\alpha^{45}\) | 89 | 01011001 | \(\alpha^{210}\) |
| 194 | 11000010 | \(\alpha^{67}\) | 165 | 10100101 | \(\alpha^{188}\) |
| 195 | 11000011 | \(\alpha^{216}\) | 53 | 00110101 | \(\alpha^{39}\) |
| 196 | 11000100 | \(\alpha^{183}\) | 101 | 01100101 | \(\alpha^{72}\) |
| 197 | 11000101 | \(\alpha^{123}\) | 184 | 10111000 | \(\alpha^{132}\) |
| 198 | 11000110 | \(\alpha^{164}\) | 163 | 10100011 | \(\alpha^{91}\) |
| 199 | 11000111 | \(\alpha^{118}\) | 158 | 10011110 | \(\alpha^{137}\) |
| 200 | 11001000 | \(\alpha^{196}\) | 210 | 11010010 | \(\alpha^{59}\) |
| 201 | 11001001 | \(\alpha^{23}\) | 247 | 11110111 | \(\alpha^{232}\) |
| 202 | 11001010 | \(\alpha^{73}\) | 98 | 01100010 | \(\alpha^{182}\) |
| 203 | 11001011 | \(\alpha^{236}\) | 90 | 01011010 | \(\alpha^{19}\) |
| 204 | 11001100 | \(\alpha^{127}\) | 133 | 10000101 | \(\alpha^{128}\) |
| 205 | 11001101 | \(\alpha^{12}\) | 125 | 01111101 | \(\alpha^{243}\) |
| 206 | 11001110 | \(\alpha^{111}\) | 168 | 10101000 | \(\alpha^{144}\) |
| 207 | 11001111 | \(\alpha^{246}\) | 58 | 00111010 | \(\alpha^{9}\) |
| 208 | 11010000 | \(\alpha^{108}\) | 41 | 00101001 | \(\alpha^{147}\) |
| 209 | 11010001 | \(\alpha^{161}\) | 113 | 01110001 | \(\alpha^{94}\) |
| 210 | 11010010 | \(\alpha^{59}\) | 200 | 11001000 | \(\alpha^{196}\) |
| 211 | 11010011 | \(\alpha^{82}\) | 246 | 11110110 | \(\alpha^{173}\) |
| 212 | 11010100 | \(\alpha^{41}\) | 249 | 11111001 | \(\alpha^{214}\) |
| 213 | 11010101 | \(\alpha^{157}\) | 67 | 01000011 | \(\alpha^{98}\) |
| 214 | 11010110 | \(\alpha^{85}\) | 215 | 11010111 | \(\alpha^{170}\) |
| 215 | 11010111 | \(\alpha^{170}\) | 214 | 11010110 | \(\alpha^{85}\) |
| 216 | 11011000 | \(\alpha^{251}\) | 16 | 00010000 | \(\alpha^{4}\) |
| 217 | 11011001 | \(\alpha^{96}\) | 115 | 01110011 | \(\alpha^{159}\) |
| 218 | 11011010 | \(\alpha^{134}\) | 118 | 01110110 | \(\alpha^{121}\) |
| 219 | 11011011 | \(\alpha^{177}\) | 120 | 01111000 | \(\alpha^{78}\) |
| 220 | 11011100 | \(\alpha^{187}\) | 153 | 10011001 | \(\alpha^{68}\) |
| 221 | 11011101 | \(\alpha^{204}\) | 10 | 00001010 | \(\alpha^{51}\) |
| 222 | 11011110 | \(\alpha^{62}\) | 25 | 00011001 | \(\alpha^{193}\) |
| 223 | 11011111 | \(\alpha^{90}\) | 145 | 10010001 | \(\alpha^{165}\) |
| 224 | 11100000 | \(\alpha^{203}\) | 20 | 00010100 | \(\alpha^{52}\) |
| 225 | 11100001 | \(\alpha^{89}\) | 63 | 00111111 | \(\alpha^{166}\) |
| 226 | 11100010 | \(\alpha^{95}\) | 230 | 11100110 | \(\alpha^{160}\) |
| 227 | 11100011 | \(\alpha^{176}\) | 240 | 11110000 | \(\alpha^{79}\) |
| 228 | 11100100 | \(\alpha^{156}\) | 134 | 10000110 | \(\alpha^{99}\) |
| 229 | 11100101 | \(\alpha^{169}\) | 177 | 10110001 | \(\alpha^{86}\) |
| 230 | 11100110 | \(\alpha^{160}\) | 226 | 11100010 | \(\alpha^{95}\) |
| 231 | 11100111 | \(\alpha^{81}\) | 241 | 11110001 | \(\alpha^{174}\) |
| 232 | 11101000 | \(\alpha^{11}\) | 250 | 11111010 | \(\alpha^{244}\) |
| 233 | 11101001 | \(\alpha^{245}\) | 116 | 01110100 | \(\alpha^{10}\) |
| 234 | 11101010 | \(\alpha^{22}\) | 243 | 11110011 | \(\alpha^{233}\) |
| 235 | 11101011 | \(\alpha^{235}\) | 180 | 10110100 | \(\alpha^{20}\) |
| 236 | 11101100 | \(\alpha^{122}\) | 109 | 01101101 | \(\alpha^{133}\) |
| 237 | 11101101 | \(\alpha^{117}\) | 33 | 00100001 | \(\alpha^{138}\) |
| 238 | 11101110 | \(\alpha^{44}\) | 178 | 10110010 | \(\alpha^{211}\) |
| 239 | 11101111 | \(\alpha^{215}\) | 106 | 01101010 | \(\alpha^{40}\) |
| 240 | 11110000 | \(\alpha^{79}\) | 227 | 11100011 | \(\alpha^{176}\) |
| 241 | 11110001 | \(\alpha^{174}\) | 231 | 11100111 | \(\alpha^{81}\) |
| 242 | 11110010 | \(\alpha^{213}\) | 181 | 10110101 | \(\alpha^{42}\) |
| 243 | 11110011 | \(\alpha^{233}\) | 234 | 11101010 | \(\alpha^{22}\) |
| 244 | 11110100 | \(\alpha^{230}\) | 3 | 00000011 | \(\alpha^{25}\) |
| 245 | 11110101 | \(\alpha^{231}\) | 143 | 10001111 | \(\alpha^{24}\) |
| 246 | 11110110 | \(\alpha^{173}\) | 211 | 11010011 | \(\alpha^{82}\) |
| 247 | 11110111 | \(\alpha^{232}\) | 201 | 11001001 | \(\alpha^{23}\) |
| 248 | 11111000 | \(\alpha^{116}\) | 66 | 01000010 | \(\alpha^{139}\) |
| 249 | 11111001 | \(\alpha^{214}\) | 212 | 11010100 | \(\alpha^{41}\) |
| 250 | 11111010 | \(\alpha^{244}\) | 232 | 11101000 | \(\alpha^{11}\) |
| 251 | 11111011 | \(\alpha^{234}\) | 117 | 01110101 | \(\alpha^{21}\) |
| 252 | 11111100 | \(\alpha^{168}\) | 127 | 01111111 | \(\alpha^{87}\) |
| 253 | 11111101 | \(\alpha^{80}\) | 255 | 11111111 | \(\alpha^{175}\) |
| 254 | 11111110 | \(\alpha^{88}\) | 126 | 01111110 | \(\alpha^{167}\) |
| 255 | 11111111 | \(\alpha^{175}\) | 253 | 11111101 | \(\alpha^{80}\) |
\(\mathbb{F}_{2^8}\)の加算は各桁を\(\mathbb{F}_2\)の上で加算することで計算される。\(\mathbb{F}_2\)の上の加算はXOR演算と同じなので、\(\mathbb{F}_{2^8}\)の加算は各桁のXOR演算となる。また、この場合も減算と加算は同じ結果になる。
例えば\(91+188\)は次のように計算することができる。(\(91-188\)も全く同じ結果になる)
\begin{align} 91+188 &= \mathrm{0b01011011} + \mathrm{10111100} \\ &= \mathrm{0b11100111} \\ &= 231 \end{align}
\(\mathbb{F}_{2^8}\)の乗算は原始元\(\alpha\)を用いた冪乗表記を経由することで簡単に計算できる。
各\(y\in\mathbb{F}_{2^8}\)に対応する\(\alpha^n\)の指数を予め保持しておくことで、\(y\)と\(n\)を相互に変換することができる。この対応を利用することで、\(y_1\times y_2 = \alpha^{n_1}\times\alpha^{n_2} = \alpha^{n_1+n_2}\)となることから\(n_1+n_2\)に対応する\(y\)を求めれば良い。
除算についても、\(\alpha^{255}=1\)となることから\(y^{-1}=\alpha^{255-n}\)と言えるので、\(y_1/y_2 = y_1\times y_2^{-1}\)を冪乗表記を経由して求めれば良い。
例えば\(91\times188\)は次のように計算することができる。
\begin{align} 91\times188 &= \alpha^{92}\times\alpha^{71} \\ &= \alpha^{163} \\ &= 99 \end{align}
また、\(91/188\)は次のように計算することができる。
\begin{align} 91/188 &= \alpha^{92}\times\alpha^{255-71} \\ &= \alpha^{255+21} \\ &= \alpha^{21} \\ &= 117 \end{align}
参考
- 先名健一 - 例題で学ぶ符号理論入門
- 岡本吉央 - 離散数理工学 第7回 離散代数:多項式環による有限体の構成
- 有限体 GF(2^n) の既約多項式および原始多項式の一覧: 1 次から 8 次まで #数学 - Qiita
- 有限体 – 標数 |その標数は必ず素数【位数は素数ベキ】 | 岩井の数学ブログ