誤り訂正符号 - BCH符号・RS符号
関連ページ
- 有限体
- 誤り訂正符号 - BCH符号・RS符号 (本ページ)
- QRコードの仕組み
- QRコード生成ツール
目次
誤り訂正符号
情報を送受信したり記録したりする際には、通信路のノイズや記録媒体の劣化により、ビット反転や欠落が発生する可能性がある。このような誤りに対処することを目的に発展してきたのが、誤り検出・訂正理論である。
最も単純な誤り検出の例がチェックサム(チェックディジット)である。例えば日本のバーコード規格であるJANコードでは、10進数の12桁からなる情報\(a_1, a_2, a_3, \cdots , a_{12}\)に対して、
\begin{align} s := a_1 + 3a_2 + a_3 + 3a_4 + \cdots + a_{11} + 3a_{12} \end{align}
を計算し、\(s+a_{13}\)が10で割り切れるように追加の桁\(a_{13}\)を付与することで、13桁のコードを生成する。この仕組みによって、仮に1桁分の誤りが発生した場合ににチェックサムの整合性が取れなくなるので、読み取ったコードが破損していることを検出できるようになる。
チェックサムの例では12桁の元データに対して13桁の値を対応付けたが、このように誤り訂正符号では「保持したい情報」(元データ)と「より冗長な情報」を一対一で対応させることで、誤りの検出・訂正を可能にする余地を生み出す。
元のデータに対応する冗長な情報のことを符号語と言い、符号語の集合のことを符号と言う。
線形符号
符号\(C\)が線形空間であるとき、符号\(C\)は線形符号であると言う。つまり線形符号\(C\)では、2つの符号語\(c_1,c_2\in C\)とスカラー\(a_1, a_2\)に対して\(a_1c_1+a_2c_2\)もまた\(C\)の符号となる。
符号理論では通常ビット列のデータを扱うので、線形符号は有限体上で実装される。
例えば\(C\subseteq\{0,1\}^n\)の場合、符号語は長さ\(n\)のビット列であり、符号語同士の加算はXOR演算で定義することで線形符号となる。(この例ではスカラー倍は0倍と1倍しかないので、スカラー倍に関して線形空間の要件を満たすことは自明)
一例として、
\begin{align} C = \{00000, 01101, 10011, 11110\} \end{align}
は線形符号になる。
線形符号の中でも特に符号語の先頭が元データと一致するものを組織符号と言う。上記の例はそれぞれ2桁の元データ00, 01, 10, 11と対応しているとすると組織符号であると言える。
更に、組織符号の元データの先頭に\(s\)個の0が連続するという制約を加えると、組織符号の符号語の先頭にも同様に\(s\)個の0が連続することになる。このとき、元データと符号語の両方で先頭から\(s\)個の0を省略することができる。このように符号の先頭を省略して得られる線形符号を短縮符号と言う。
生成行列
\(\mathbb{F}_q\)を位数\(q\)の有限体とし、線形符号\(C\)は\(C\subseteq\mathbb{F}_{q^n}\)から構成されているとする。このとき、\(C\)は\(n\)次元線形空間の部分空間なので\(n\)個以下の直交基底が存在する。直交基底の個数を\(k\leq n\)とし、直交基底を\(\{g^{(j)}\}_{j=1}^k\subseteq C\)と表す。
規定の性質から、任意の符号語\(c\in C\)は基底\(g^{(1)}, g^{(2)}, \cdots , g^{(k)}\in C\)と一意な係数\(u_1, u_2, \cdots , u_k\in\mathbb{F}_q\)によって、
\begin{align} c = u_1g^{(1)} + u_2g^{(2)} + \cdots u_kg^{(k)} \end{align}
と線形結合で表すことができる。また、逆に係数を任意に取っても、線形空間の性質から\(c\)は\(C\)の符号語となる。
ここで、\(n\times k\)行列\(G\)の各成分を\(G_{ij}=g^{(j)}_i\in\mathbb{F}_q\)となるように定める。このように構成した\(\mathbb{F}_q\)値行列\(G\)を生成行列と言う。(ただし、一般的には\(G\)ではなく\(G^\top\)を生成行列と定義することが多い)
列ベクトル\(u\)の各成分を\(u_j\)とすると、上記の関係は、
\begin{align} c=Gu \end{align}
と表すこともできる。
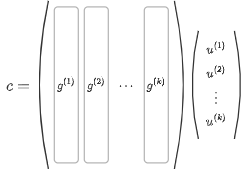
したがって、\(c\in C\)と\(u\in\mathbb{F}_q^k\)は一対一に対応していると言える。
\(u\)には\(q\)進数\(k\)桁の任意の値を取ることができるので、\(u\)を変換したい元データとすることで、生成行列を用いて符号語\(c\)に変換することができる。
検査行列
符号語に誤りが発生した場合を考える。
つまり、\(c\in C\)の一部の成分が異なる値に変化して、\(c+e\in\mathbb{F}_q^n\backslash C\)となったとする。
\(C\)は\(\mathbb{F}_q^n\)の部分線形空間なので、\(C\)の直交基底\(\{g^{(j)}\}_{j=1}^k\)に\(n-k\)個のベクトル\(\{h^{(j)}\}_{j=1}^{n-k}\subseteq \mathbb{F}_q^n\)を追加して、\(\mathbb{F}_q^n\)の直交基底にすることができる。
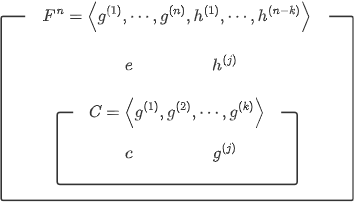
\(F^n\)の基底の関係
このとき、誤りのない符号語\(c\in C\)は前述のように\(\{g^{(j)}\}_{j=1}^k\)の線形結合で表すことができるので、どんな\(h^{(j)}\)とも直交する。つまり、どんな\(j\)に対しても\(c\cdot h^{(j)}=0\)となる。
一方、誤りを含んだベクトル\(c+e\in \mathbb{F}_q^n\backslash C\)は\(\{g^{(j)}\}_{j=1}^k\)の線形結合で表すことはできないので、必ず1つ以上の\(h^{(j)}\)の成分を持つ。つまり、\((c+e)\cdot h^{(j)}\neq0\)となるような\(j\)が存在する。
したがって、受信語\(r=c+e\)(\(e\)は0の場合も含む)に誤りが存在するかどうかは次のように判定することができる。
- 全ての\(j\)に対して\(r\cdot h^{(j)}=0\) ⇒ \(r\)には誤りがない
- \(r\cdot h^{(j)}\neq0\)となる\(j\)が存在 ⇒ \(r\)には誤りがある
ここで、追加された基底\(\{h^{(j)}\}_{j=1}^{n-k}\subseteq \mathbb{F}_q^n\)を用いて、\((n-k)\times n\)行列\(H\)の各成分を\(H_{ij}=h^{(i)}_j\in\mathbb{F}_q\)となるように定める。このように構成した\(\mathbb{F}_q\)値行列\(H\)を検査行列と言う。
上記の判定法は行列を使って表すと、符号語\(r\)に検査行列\(H\)を作用させて
\begin{align} s:&=Hr \\ &=H(c+e) \\ &=Hc+He \\ &=0+He \\ &=He \\ \end{align}
としたときに、\(s=0\)ならば誤りなし、\(s\neq0\)ならば誤りありと判定できるということになる。ここで、\(s\in \mathbb{F}_q^{n-k}\)はシンドロームと呼ばれるベクトルである。
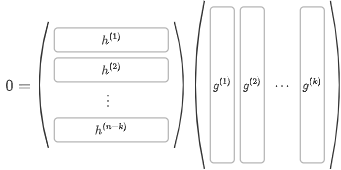
検査行列
最小距離
線形空間\(\mathbb{F}_q^n\)にはHamming距離と呼ばれる距離関数を導入することができる。Hamming距離\(d_H(c_1,c_2)\)は、2つの符号語\(c_1, c_2\)の値の異なる成分の個数と定義される。例えば\((1, 0, 5, 6, 2)\)と\((1, 4, 5, 6, 3)\)のHamming距離は\(2\)である。
Hamming距離は\(c_1-c_2\)の0ではない成分の数と捉えることもできる。つまり、\(d_H(c_1,c_2)=d_H(c_1-c_2,0)\)となる。ここで、Hamming重みを\(w_H(c)=d_H(c,0)\)と定義すると、\(d_H(c_1,c_2)=w_H(c_1-c_2)\)となる。
\(C\)の異なる要素同士の距離の最小値
\begin{align} d:=\min\left\{d_H(c_1,c_2)|c_1,c_2\in C, c_1\neq c_2\right\} \end{align}
を最小距離と言う。最小距離は0以外の最小のHamming重み\(\min\left\{w_H(c)|c\in C\backslash\{0\}\right\}\)と一致する。
符号語\(c\)に\(d-1\)個以下の誤りが付与されて受信語\(r\)となったとする。このとき、\(r\in C\)と仮定すると\(d_H(c,r)\leq d-1\)となって\(d\)が最小距離であることと矛盾するので、\(r\in \mathbb{F}_q^n\backslash C\)である。
したがって、最小距離\(d\)の符号では\(d-1\)個までの誤りが付与された受信語\(r\)は\(C\)に含まれることはないので、検査行列を作用させることで誤りのある受信語であると判定することができる。言い換えると、\(d-1\)個までの誤り検出ができることになる。
また誤り訂正については、誤りを含んだ受信語\(r\)に対して、\(r\)に最も近い符号語\(c\)を選択する復号法を考える。誤りの個数を\(t\)としたとき、\(t<d-t\)となれば正しく復号することができ、そうでなければ誤った符号語に復号されてしまう可能性がある。\(t<d-t\)を解くと、
\begin{align} t < \frac{d}{2} \end{align}
となるので、\(t\)の最大値は\(\lfloor\frac{d-1}{2}\rfloor\)となる。つまり、最小距離\(d\)の符号では\(\lfloor\frac{d-1}{2}\rfloor\)個までの誤りを訂正できる。逆に言えば、\(t\)個の誤りを訂正できるようにしたい場合、最小距離が\(d=2t+1\)以上になるように線形符号を構成すれば良い。

最小距離7の例
このとき3つまでの誤りが発生しても元の符号が一意に定まる
まとめ
線形符号\(C\subseteq\mathbb{F}_q^n\)では、直交基底から生成行列\(G\)を構成することで、任意の元データ\(u\in \mathbb{F}_q^k\)から符号\(c=Gu\)を生成することができる。
また、\(\mathbb{F}_q^n\)全体の直交基底となるように追加されたベクトルから検査行列\(H\)を構成すると、受信語\(r\)の誤りの有無を\(s:=Hr\)が0となるかどうかによって判定することができる。
線形符号の最小距離(Hamming距離の最小値)を\(d\)とするとき、
- 誤り検出は\(d-1\)個まで
- 誤り訂正は\(\lfloor\frac{d-1}{2}\rfloor\)個まで
可能である。
なお、符号の長さ\(n\)、元データの長さ\(k\)、最小距離\(d\)の符号を(n,k,d)符号と表記することがある。
巡回符号
線形符号\(C\)の符号語\(c=(c_1, c_2, \cdots , c_{n-1}, c_n)\)に対して、その各桁を左にずらした\((c_2, c_3, \cdots , c_n, c_1)\)もまた\(C\)の符号となるとき、符号\(C\)は巡回符号であると言う。
巡回符号は多項式を用いて表現することができる。
有限体\(\mathbb{F}_q\)に対して\(\mathbb{F}_q[y]/(y^n-1)\)という可換環を考える。(\(y^n-1\)は既約ではないので\(\mathbb{F}_q[y]/(y^n-1)\)は有限体にならないことに注意)
以後、巡回符号の符号語\(c=(c_{n-1}, c_{n-2}, \cdots , c_1, c_0)\)に対して、\(\mathbb{F}_q\)上の多項式
\begin{align} c(y) := c_{n-1}y^{n-1} + c_{n-2}y^{n-2} + \cdots + c_1y + c_0 \end{align}
を対応させる。(次数と添字を揃えている)
巡回符号の多項式の集合を\(C\subseteq \mathbb{F}_q[y]/(y^n-1)\)と表す。
生成多項式・検査多項式
上記の多項式に\(y\)を掛けると、
\begin{align} c(y)y &= c_{n-1}y^n + c_{n-2}y^{n-1} + \cdots + c_1y^2 + c_0y \\ &= c_{n-1}(y^n-1) + c_{n-1} + c_{n-2}y^{n-1} + \cdots + c_1y^2 + c_0y \\ &\equiv 0 + c_{n-1} + c_{n-2}y^{n-1} + \cdots + c_1y^2 + c_0y \\ &= c_{n-2}y^{n-1} + c_{n-3}y^{n-2} + \cdots + c_0y + c_{n-1} \\ \end{align}
となり、巡回符号の定義からこの多項式もまた\(C\)に含まれる。
これは何度繰り返しても同様なので、\(c(y)\in C\)のとき任意の自然数\(i\)に対して\(c(y)y^i\in C\)となると言える。
更に線形符号の性質から、任意の多項式\(u(y) = u_{k-1}y^{k-1} + u_{k-2}y^{k-2} + \cdots u_1y + u_0\)に対しても、\(c(y)u(y)\in C\)となる。
\(C\)の(0を除く)最小次数の多項式を\(g(y)\)とする。
任意の\(c(y)\in C\)を取り、\(c(y)\)を\(g(y)\)で割って余り\(r(y)\)を求める。このとき、\(c(y)=u(y)g(y)+r(y)\)となるので、線形符号の性質から\(r(y)\)もまた\(C\)の符号語となる。
しかし、\(r(y)\neq 0\)とすると\(g(y)\)が最小次数であることと矛盾するので、\(r(y)=0\)にしかなり得ない。したがって、任意の\(c(y)\)に対して\(c(y)=u(y)g(y)\)となるような多項式\(u(y)\)が存在すると言える。
このことから、巡回符号の符号語\(c(y)\in C\)と多項式\(u(y)\)が一対一に対応していることがわかる。
\(g(y)\)の次数を\(n-k\)とすると、\(u(y)\)は全ての\(k-1\)次の多項式から選ぶことができる。つまり、元データ\(u\)を\(F\)値\(k\)桁の値から任意に取って、巡回符号の符号語\(c\)を生成することができることになる。
このとき、\(C\)の多項式\(g(y)\)を生成多項式と言い、線形符号の生成行列と同じ役割を持つ。なお、生成多項式は既約である必要はない。
生成多項式\(g(y)\)に\(y^k\)を掛けると、
\begin{align} g(y)y^k &= \left(g_{n-k}y^{n-k} + g_{n-k-1}y^{n-k-1} + \cdots g_1y + g_0\right)y^k \\ &= g_{n-k}y^n + g_{n-k-1}y^{n-1} + \cdots + g_1y^{k+1} + g_0y^k \\ &= g_{n-k}(y^n-1) + g_{n-k} + g_{n-k-1}y^{n-1} + \cdots + g_1y^{k+1} + g_0y^k \\ \end{align}
となるが、前述の性質から\(g_{n-k} + g_{n-k-1}y^{n-1} + \cdots + g_1y^{k+1} + g_0y^k = u(y)g(y)\)となるような\(u(y)\)が存在する。したがって、
\begin{align} g(y)y^k &= g_{n-k}(y^n-1) + g_{n-k} + g_{n-k-1}y^{n-1} + \cdots + g_1y^{k+1} + g_0y^k \\ &= g_{n-k}(y^n-1) + u(y)g(y) \\ \end{align}
つまり
\begin{align} g_{n-k}^{-1}(y^k-u(y))g(y) = y^n-1 \\ \end{align}
となるので、\(g(y)\)は\(y^n-1\)を割り切るような多項式でなければならないことがわかる。そこで、検査多項式を\(h(y):=(y^n-1)/g(y)\)とする。
任意の符号語\(c(y)\)に対して、
\begin{align} c(y)h(y) &= u(y)g(y)h(y) \\ &= u(y)(y^n-1) \\ &\equiv 0 \end{align}
となることから、検査行列と同様に、\(h(y)\)を掛けた結果が0になるかどうかで受信語の誤りの有無を判定することができる。
組織符号化
生成多項式\(g(y)\)で割り切ることのできる多項式は巡回符号\(C\)の符号語となる。
そこで、任意の\(k-1\)次以下の多項式\(v(y)=v_{k-1}y^{k-1}+\cdots+v_0\)に対して、\(v(y)y^{n-k}\)を\(g(y)\)で割ると、
\begin{align} v(y)y^{n-k} = u(y)g(y) + r(y) \end{align}
と表すことができる。ここで余り\(r(y)\)は\(n-k-1\)次以下の多項式である。
したがって、
\begin{align} v(y)y^{n-k} - r(y) = u(y)g(y) \end{align}
が成り立ち、\(c(y) := v(y)y^{n-k} - r(y)\)は\(g(y)\)で割り切れるので巡回符号\(C\)の符号語となる。
\(v(y)\)の各係数を\((v_{k-1}, v_{k-2}, \cdots , v_0)\)、\(r(y)\)の各係数を\((r_{n-k-1}, r_{n-k-2}, \cdots , r_0)\)とすると、\(c(y)\)の係数は\((v_{k-1}, v_{k-2}, \cdots , v_0, -r_{n-k-1}, -r_{n-k-2}, \cdots , -r_0)\)となり、\(v(y)\)と\(-r(y)\)を結合した形になっている。
\(v(y)\)が与えられたときは上記のように\(u(y)\)が得られ、\(u(y)\)が与えられたときは\(u(y)g(y)\)の\(n-k\)次以上の部分だけを見れば\(v(y)\)が得られる。よって、\(v(y)\)と\(u(y)\)(と\(c(y)\))は一対一に対応していると言える。
元データを\(v(y)\)とすれば、上記の符号化によって符号語の先頭は\(v(y)\)と一致するので、これは組織符号となっている。
まとめ
巡回符号\(C\)は有限体\(\mathbb{F}_q\)上の多項式環\(\mathbb{F}_q[y]/(y^n-1)\)の部分線形空間として表現することができ、多項式の係数を列挙したものが符号語となる。(便宜上、多項式そのものも符号語として扱う)
\(C\)の(0を除く)最小次数の多項式\(g(y)\)を生成多項式と言う。このとき、次のような性質が成り立つ。
- 任意の多項式\(u(y)\)に対して\(u(y)g(y)\in C\)
- 任意の符号語\(c(y)\in C\)に対して、\(c(y)=u(y)g(y)\)となるような\(u(y)\)が存在
- \(g(y)\)は\(y^n-1\)を割り切る
また、\(c(y)=u(y)g(y)\)として符号化する方法の他に、長さ\(k\)の元データ\(v(y)\)に対して\(c(y)=v(y)y^{n-k}-r(y)\)とすることでも\(v(y)\)を\(c(y)\)に符号化できる。(\(r(y)\)は\(v(y)y^{n-k}\)を\(g(y)\)で割った余り)
これは組織符号となる。
BCH符号
BCH符号(Bose-Chaudhuri-Hocquenghem符号)は、1959年と1960年にHocquenghem、Bose、およびChaudhuriによって考案された巡回符号の一種。根の指数が連続するように生成多項式\(g(y)\)を選択することによって、任意の最小距離を持つ符号を構成することができる。
身近な例では、衛星通信、フラッシュメモリに利用されている。
連続する根による検査行列
\(\mathbb{F}_q\)を位数\(q\)の有限体とし、\(\mathbb{F}_q[x]\)から\(m\)次の原始多項式を取って\(f(x)\)と表す。
原始多項式の性質から、\(\mathbb{F}_{q^m}:=\mathbb{F}_q[x]/(f(x))\)は位数\(q^m\)の体となり、\(\alpha(x)=x\)が\(\mathbb{F}_{q^m}\)の原始元になる。
\(n\)を\(q^m-1\)の約数とする。
\(\frac{q^m-1}{n}\)は自然数なので、\(\beta:=\alpha^{(q^m-1)/n}\)を定めることができる。
このとき、\(\beta^n=\alpha^{q^m-1}=1\)が成り立ち、\(1, \beta, \beta^2, \cdots, \beta^{n-1}\)は全て異なる値を取る。また、\(\beta\)の任意の冪乗に対しても
\begin{align} \left(\beta^k\right)^n&=\left(\beta^n\right)^k\\ &=1^k\\ &=1 \end{align}
が成り立つ。
したがって、多項式\(y^n-1\)を\(\mathbb{F}_{q^m}\)の多項式と捉えると、その\(n\)個の根は\(\{1, \beta, \beta^2, \cdots, \beta^{n-1}\}\subseteq\mathbb{F}_{q^m}\)となる。
ここで\(y^n-1\)を
\begin{align} y^n-1 = m^{(1)}(y)m^{(2)}(y)\cdots m^{(K)}(y) \end{align}
と因数分解すると、\(y^n-1\)の根\(\{1, \beta, \beta^2, \cdots, \beta^{n-1}\}\)はそれぞれいずれかの\(m^{(k)}(y)\)の根に分類されることになる。
例えば、\(q=2, m=6, f(x)=x^6+x+1\)の場合を考えてみよう。\(q^m-1 = 2^6-1 = 63\)なので、\(n=21\)を選択することにする。
このとき、\(\beta:=\alpha^{63/21}=\alpha^3\)とすると、\(y^n-1=y^{21}-1\)の根は\(\{1, \beta, \beta^2, \cdots , \beta^{20}\}\)となる。2進表記で表すと、次の表のようになる。(計算過程は省略)
| 冪乗表記 | 2進表記 |
|---|---|
| 1 | 000001 |
| \(\beta=\alpha^3\) | 001000 |
| \(\beta^2=\alpha^6\) | 000011 |
| \(\beta^3=\alpha^9\) | 011000 |
| \(\beta^4=\alpha^{12}\) | 000101 |
| \(\beta^5=\alpha^{15}\) | 101010 |
| \(\beta^6=\alpha^{18}\) | 001111 |
| \(\beta^7=\alpha^{21}\) | 111011 |
| \(\beta^8=\alpha^{24}\) | 010001 |
| \(\beta^9=\alpha^{27}\) | 001110 |
| \(\beta^{10}=\alpha^{30}\) | 110011 |
| \(\beta^{11}=\alpha^{33}\) | 010010 |
| \(\beta^{12}=\alpha^{36}\) | 010110 |
| \(\beta^{13}=\alpha^{39}\) | 110110 |
| \(\beta^{14}=\alpha^{42}\) | 111010 |
| \(\beta^{15}=\alpha^{45}\) | 011001 |
| \(\beta^{16}=\alpha^{48}\) | 001101 |
| \(\beta^{17}=\alpha^{51}\) | 101011 |
| \(\beta^{18}=\alpha^{54}\) | 010111 |
| \(\beta^{19}=\alpha^{57}\) | 111110 |
| \(\beta^{20}=\alpha^{60}\) | 111001 |
\(y^{21}-1\)は\(\mathbb{F}_2\)係数多項式としては
\begin{align} y^{21}-1 &= (y+1)(y^2+y+1)(y^3+y+1)(y^3+y^2+1)(y^6+y^4+y^2+y+1)(y^6+y^5+y^4+y^2+1) \end{align}
と因数分解される。
因数をそれぞれ\(m^{(1)}(y), m^{(2)}(y), \cdots, m^{(6)}(y)\)と表す。(因数の添字の順番は異なっても良い)
\(y^{21}-1\)の根\(\{1, \beta, \beta^2, \cdots , \beta^{20}\}\)は、それぞれ次の表のように分類される。(実際に代入すると各項が上記の\(\beta\)の冪乗になることから、足して0になることが確認できる)
| 多項式 | 根 |
|---|---|
| \(m^{(1)}(y) = y+1\) | \(1\) |
| \(m^{(2)}(y) = y^2+y+1\) | \(\beta^7, \beta^{14}\) |
| \(m^{(3)}(y) = y^3+y+1\) | \(\beta^9, \beta^{15}, \beta^{18}\) |
| \(m^{(4)}(y) = y^3+y^2+1\) | \(\beta^3, \beta^6, \beta^{12}\) |
| \(m^{(5)}(y) = y^6+y^4+y^2+y+1\) | \(\beta, \beta^2, \beta^4, \beta^8, \beta^{11}, \beta^{16}\) |
| \(m^{(6)}(y) = y^6+y^5+y^4+y^2+1\) | \(\beta^5, \beta^{10}, \beta^{13}, \beta^{17}, \beta^{19}, \beta^{20}\) |
因数\(m^{(1)}(y), m^{(2)}(y), \cdots , m^{(K)}(y)\)から幾つか選んで掛けることで\(g(y)\)を構成する。このとき、各因数の根が\(g(y)\)の根となる。
ここで、\(g(y)\)の根の中で\(\beta\)の指数が連続するものを探す。(ループをまたいでも良い)
例えば上の例の場合、\(g(y):=m^{(4)}(y)m^{(5)}(y)\)とすると\(g(y)\)の根は\(\beta, \beta^2, \beta^3, \beta^4, \beta^6, \beta^8, \beta^{11}, \beta^{12}, \beta^{16}\)となって、\(\beta, \beta^2, \beta^3, \beta^4\)の4つは指数が連続している。
\(g(y)\)に\(h\)個の連続する根\(\beta^{a}, \beta^{a+1}, \cdots , \beta^{a+h-1}\)が存在するとき、各\(0\leq i\leq h-1\)に対して\(g\left(\beta^{a+i}\right)=0\)なので符号語\(c(y)\)に対しても
\begin{align} c\left(\beta^{a+i}\right)&=u\left(\beta^{a+i}\right)g\left(\beta^{a+i}\right)\\ &=u\left(\beta^{a+i}\right)\cdot0\\ &=0 \end{align}
が成り立つ。これをベクトルで表記すると、
\begin{align} \begin{pmatrix} \beta^{(n-1)(a+i)} & \beta^{(n-2)(a+i)} & \cdots & \beta^{2(a+i)} & \beta^{a+i} & 1 \end{pmatrix}\cdot \begin{pmatrix} c_{n-1} \\ c_{n-2} \\ \vdots \\ c_2 \\ c_1 \\ c_0 \\ \end{pmatrix} = 0 \end{align}
となる。
したがって、\(\mathbb{F}_{q^m}\)値行列\(H\)を次のように定義すると、任意の符号語に作用させた結果は0となる。
(ここでは高次を左側にするという規則で表現しているが、一般的には下の表記とは左右逆になっていることが多い)
\begin{align} H = \begin{pmatrix} \beta^{(n-1)a} & \beta^{(n-2)a} & \cdots & \beta^{2a} & \beta^a & 1 \\ \beta^{(n-1)(a+1)} & \beta^{(n-2)(a+1)} & \cdots & \beta^{2(a+1)} & \beta^{a+1} & 1 \\ \beta^{(n-1)(a+2)} & \beta^{(n-2)(a+2)} & \cdots & \beta^{2(a+2)} & \beta^{a+2} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ \beta^{(n-1)(a+h-1)} & \beta^{(n-2)(a+h-1)} & \cdots & \beta^{2(a+h-1)} & \beta^{a+h-1} & 1 \end{pmatrix} \end{align}
\(H\)から任意の\(h\)列を取り出して\(H_h\)とし、その行列式を計算する。
\begin{align} \det(H_h) &= \begin{vmatrix} \beta^{k_1a} & \beta^{k_2a} & \cdots & \beta^{k_{h-1}a} & \beta^{k_ha} \\ \beta^{k_1(a+1)} & \beta^{k_2(a+1)} & \cdots & \beta^{k_{h-1}(a+1)} & \beta^{k_h(a+1)} \\ \beta^{k_1(a+2)} & \beta^{k_2(a+2)} & \cdots & \beta^{k_{h-1}(a+2)} & \beta^{k_h(a+2)} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \beta^{k_1(a+h-1)} & \beta^{k_2(a+h-1)} & \cdots & \beta^{k_{h-1}(a+h-1)} & \beta^{k_h(a+h-1)} \end{vmatrix} \\ &= \beta^{k_1a} \beta^{k_2a} \cdots \beta^{k_{h-1}a} \beta^{k_ha} \begin{vmatrix} 1 & 1 & \cdots & 1 & 1 \\ \beta^{k_1} & \beta^{k_2} & \cdots & \beta^{k_{h-1}} & \beta^{k_h} \\ \beta^{k_1\cdot2} & \beta^{k_2\cdot2} & \cdots & \beta^{k_{h-1}\cdot2} & \beta^{k_h\cdot2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \beta^{k_1(h-1)} & \beta^{k_2(h-1)} & \cdots & \beta^{k_{h-1}(h-1)} & \beta^{k_h(h-1)} \end{vmatrix} \\ \end{align}
ここで、2行目の行列式はVandermondeの行列式と呼ばれる。
次のように定義される行列式をVandermondeの行列式と言う。
\begin{align} \det(V_n) &:= \begin{vmatrix} 1 & 1 & \cdots & 1 & 1 \\ x_1 & x_2 & \cdots & x_{n-1} & x_n \\ x_1^2 & x_2^2 & \cdots & x_{n-1}^2 & x_n^2 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_1^{n-1} & x_2^{n-1} & \cdots & x_{n-1}^{n-1} & x_n^{n-1} \\ \end{vmatrix} \\ &= \begin{vmatrix} 1 & 1 & \cdots & 1 & 1 \\ x_1-x_n & x_2-x_n & \cdots & x_{n-1}-x_n & 0 \\ x_1^2-x_n^2 & x_2^2-x_n^2 & \cdots & x_{n-1}^2-x_n^2 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_1^{n-1}-x_n^{n-1} & x_2^{n-1}-x_n^{n-1} & \cdots & x_{n-1}^{n-1}-x_n^{n-1} & 0 \\ \end{vmatrix} \\ &= (-1)^{n-1} \begin{vmatrix} x_1-x_n & x_2-x_n & \cdots & x_{n-1}-x_n \\ x_1^2-x_n^2 & x_2^2-x_n^2 & \cdots & x_{n-1}^2-x_n^2 \\ \vdots & \vdots & \ddots & \vdots \\ x_1^{n-1}-x_n^{n-1} & x_2^{n-1}-x_n^{n-1} & \cdots & x_{n-1}^{n-1}-x_n^{n-1} \\ \end{vmatrix} \\ &= (-1)^{n-1}\left(\prod_{1\leq i< n}(x_i-x_n)\right) \begin{vmatrix} 1 & 1 & \cdots & 1 \\ x_1+x_n & x_2+x_n & \cdots & x_{n-1}+x_n \\ \vdots & \vdots & \ddots & \vdots \\ \sum_{k=0}^{n-2}x_1^{n-2-k}x_n^k & \sum_{k=0}^{n-2}x_2^{n-2-k}x_n^k & \cdots & \sum_{k=0}^{n-2}x_{n-1}^{n-2-k}x_n^k \\ \end{vmatrix} \\ &= \left(\prod_{1\leq i< n}(x_n-x_i)\right) \begin{vmatrix} 1 & 1 & \cdots & 1 \\ x_1+x_n & x_2+x_n & \cdots & x_{n-1}+x_n \\ \vdots & \vdots & \ddots & \vdots \\ \sum_{k=0}^{n-2}x_1^{n-2-k}x_n^k & \sum_{k=0}^{n-2}x_2^{n-2-k}x_n^k & \cdots & \sum_{k=0}^{n-2}x_{n-1}^{n-2-k}x_n^k \\ \end{vmatrix} \\ \end{align}
ここで最後の行列式の第\(i+1\)列に注目すると、
\begin{align} & \begin{vmatrix} 1 & 1 & \cdots & 1 \\ x_1+x_n & x_2+x_n & \cdots & x_{n-1}+x_n \\ \vdots & \vdots & & \vdots \\ \sum_{k=0}^ix_1^{i-k}x_n^k & \sum_{k=0}^ix_2^{i-k}x_n^k & \cdots & \sum_{k=0}^ix_{n-1}^{i-k}x_n^k \\ \vdots & \vdots & & \vdots \\ \sum(\cdots) & \sum(\cdots) & \cdots & \sum(\cdots) \\ \end{vmatrix} \\ =& \begin{vmatrix} \vdots & \vdots & & \vdots \\ x_1^i+\sum_{k=1}^ix_1^{i-k}x_n^k & x_2^i+\sum_{k=1}^ix_2^{i-k}x_n^k & \cdots & x_{n-1}^i+\sum_{k=1}^ix_{n-1}^{i-k}x_n^k \\ \vdots & \vdots & & \vdots \\ \end{vmatrix} \\ =& \begin{vmatrix} \vdots & \vdots & & \vdots \\ x_1^i & x_2^i & \cdots & x_{n-1}^i \\ \vdots & \vdots & & \vdots \\ \end{vmatrix} +\sum_{k=1}^i \begin{vmatrix} \vdots & \vdots & & \vdots \\ x_1^{i-k}x_n^k & x_2^{i-k}x_n^k & \cdots & x_{n-1}^{i-k}x_n^k \\ \vdots & \vdots & & \vdots \\ \end{vmatrix} \\ =& \begin{vmatrix} \vdots & \vdots & & \vdots \\ x_1^i & x_2^i & \cdots & x_{n-1}^i \\ \vdots & \vdots & & \vdots \\ \end{vmatrix} +\sum_{k=1}^ix_n^k \begin{vmatrix} \vdots & \vdots & & \vdots \\ x_1^{i-k} & x_2^{i-k} & \cdots & x_{n-1}^{i-k} \\ \vdots & \vdots & & \vdots \\ \end{vmatrix} \\ \end{align}
となるが、\(x_1^{i-k}, x_2^{i-k}, \cdots, x_{n-1}^{i-k}\)の列はそれより上に完全に一致する列が存在するので総和部分の行列式は全て0になる。
したがって、
\begin{align} \det(V_n) &= \begin{vmatrix} 1 & 1 & 1 & \cdots & 1 \\ x_1 & x_2 & x_3 & \cdots & x_n \\ x_1^2 & x_2^2 & x_3^2 & \cdots & x_n^2 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_1^{n-1} & x_2^{n-1} & x_3^{n-1} & \cdots & x_n^{n-1} \\ \end{vmatrix} \\ &= \left(\prod_{1\leq i< n}(x_n-x_i)\right) \begin{vmatrix} 1 & 1 & \cdots & 1 \\ x_1+x_n & x_2+x_n & \cdots & x_{n-1}+x_n \\ \vdots & \vdots & \ddots & \vdots \\ \sum_{k=0}^{n-2}x_1^{n-2-k}x_n^k & \sum_{k=0}^{n-2}x_2^{n-2-k}x_n^k & \cdots & \sum_{k=0}^{n-2}x_{n-1}^{n-2-k}x_n^k \\ \end{vmatrix} \\ &= \left(\prod_{1\leq i< n}(x_n-x_i)\right) \begin{vmatrix} 1 & 1 & \cdots & 1 \\ x_1 & x_2 & \cdots & x_{n-1} \\ \vdots & \vdots & \ddots & \vdots \\ x_1^{n-2} & x_2^{n-2} & \cdots & x_{n-1}^{n-2} \\ \end{vmatrix} \\ &= \left(\prod_{1< j\leq n}(x_j-x_1)\right)\det(V_{n-1}) \end{align}
となり、これを繰り返し適用すると次の結果が得られる。
\begin{align} \det(V_n) &= \left(\prod_{1\leq i< n}(x_n-x_i)\right)\left(\prod_{1\leq i< n-1}(x_{n-1}-x_i)\right)\cdots\left(\prod_{1\leq i< 3}(x_3-x_i)\right) \begin{vmatrix} 1 & 1 \\ x_1 & x_2 \end{vmatrix} \\ &= \left(\prod_{1\leq i< n}(x_n-x_i)\right)\left(\prod_{1\leq i< n-1}(x_{n-1}-x_i)\right)\cdots\left(\prod_{1\leq i< 3}(x_3-x_i)\right)\left(\prod_{1\leq i< 2}(x_2-x_i)\right) \\ &= \prod_{1\leq i< j\leq n}(x_j-x_i) \end{align}
\(H\)のVandermondeの行列式は
\begin{align} \begin{vmatrix} 1 & 1 & \cdots & 1 & 1 \\ \beta^{k_1} & \beta^{k_2} & \cdots & \beta^{k_{h-1}} & \beta^{k_h} \\ \beta^{k_1\cdot2} & \beta^{k_2\cdot2} & \cdots & \beta^{k_{h-1}\cdot2} & \beta^{k_h\cdot2} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ \beta^{k_1(h-1)} & \beta^{k_2(h-1)} & \cdots & \beta^{k_{h-1}(h-1)} & \beta^{k_h(h-1)} \end{vmatrix} = \prod_{1\leq i< j\leq h}(\beta^{k_j}-\beta^{k_i}) \end{align}
となるが、\(\beta^{k_j}, \beta^{k_i}\)は\(k_i, k_j\in\{0, 1, 2, \cdots, n-1\}\)なので常に\(\beta^{k_j}\neq\beta^{k_i}\)となる。よってVandermondeの行列式は0にならないので、\(H_h\)の行列式も0にならない。
これは、\(H\)の任意の\(h\)列が一次独立であることを意味する。
言い換えると、符号語\(c\)に誤り\(e\)が発生して受信語\(r=c+e\)となったとき、誤りの個数が1個以上\(h\)個以下ならば(=\(e\)の成分で0でないものが\(h\)個以下ならば)、\(s=Hr=Hc+He=He\)が0になることはないということになる。
したがって\(s=Hr\)によって\(h\)個までの誤りを検出できることがわかる。(最小距離が\(h+1\)以上であると言える)
このように、行列\(H\)は検査行列のように機能する。
線形符号の通常の検査行列は\(\mathbb{F}_q\)値だが、こちらの検査行列\(H\)は\(\mathbb{F}_{q^n}\)値であることに注意。
符号化
BCH符号では、上記のように生成多項式を構成して符号化を行う。
位数\(q\)の有限体\(\mathbb{F}_q\)と自然数\(m\)に対して、符号長\(n\)は\(q^m-1\)を割り切るように設定される。(符号\(C\)は\(\mathbb{F}_q^n\)の部分空間)
\(\mathbb{F}_{q^m}\)に含まれる位数\(n\)の元を\(\beta\)とする。\(y^n-1\)を因数分解して、\(\beta\)の指数が連続になるような根を持つ因数を選んで\(n-k\)次生成多項式\(g(y)\)を構成する。
検査行列\(H\)は\(\mathbb{F}_q\)値ではなく、\(\mathbb{F}_{q^m}\)値の行列として実装される。
2つの例を見てみよう。
例1 (QRコードのFormat Informationで使われるBCH符号)
\(q=2, m=4\)の場合を考える。
\(\mathbb{F}_2\)係数の4次原始多項式\(f(x)=x^4+x+1\)を選択し、\(\mathbb{F}_{2^4}\)を構成する。また、\(\mathbb{F}_{2^4}\)の原始元を\(\alpha(x)=x\)とする。
\(2^4-1=3\times5\)なので\(n=15\)を選択し、\(\beta = \alpha\)とする。\(\beta\)の冪乗は次の表の通り。
| 冪乗表記 | 2進表記 |
|---|---|
| 1 | 0001 |
| \(\beta^1=\alpha^1\) | 0010 |
| \(\beta^2=\alpha^2\) | 0100 |
| \(\beta^3=\alpha^3\) | 1000 |
| \(\beta^4=\alpha^4\) | 0011 |
| \(\beta^5=\alpha^5\) | 0110 |
| \(\beta^6=\alpha^6\) | 1100 |
| \(\beta^7=\alpha^7\) | 1011 |
| \(\beta^8=\alpha^8\) | 0101 |
| \(\beta^9=\alpha^9\) | 1010 |
| \(\beta^{10}=\alpha^{10}\) | 0111 |
| \(\beta^{11}=\alpha^{11}\) | 1110 |
| \(\beta^{12}=\alpha^{12}\) | 1111 |
| \(\beta^{13}=\alpha^{13}\) | 1101 |
| \(\beta^{14}=\alpha^{14}\) | 1001 |
\(y^n-1 = y^{15}-1\)は次のように因数分解され、各因数に対して\(\beta\)の冪乗は表のように分類される。
\begin{align} y^{15} - 1 &= (y+1)(y^2+y+1)(y^4+y+1)(y^4+y^3+1)(y^4+y^3+y^2+y+1) \end{align}
| 多項式 | 根 |
|---|---|
| \(y+1\) | \(1\) |
| \(y^2+y+1\) | \(\beta^5, \beta^{10}\) |
| \(y^4+y+1\) | \(\beta, \beta^2, \beta^4, \beta^8\) |
| \(y^4+y^3+1\) | \(\beta^7, \beta^{11}, \beta^{13}, \beta^{14}\) |
| \(y^4+y^3+y^2+y+1\) | \(\beta^3, \beta^6, \beta^9, \beta^{12}\) |
生成多項式\(g(y)\)を
\begin{align} g(y) &= (y^2+y+1)(y^4+y+1)(y^4+y^3+y^2+y+1) \\ &= y^{10}+y^8+y^5+y^4+y^2+y+1 \end{align}
と選択することで、\(g(y)\)には6つの連続する根\(\beta,\beta^2,\beta^3,\beta^4,\beta^5,\beta^6\)が含まれる。したがって、このBCH符号の最小距離は7以上になる。また、\(g(y)\)は10次なので、このBCH符号は\((n,k)=(15,5)\)符号となる。
この10次の生成多項式では5-bitの元データを符号化することができる。
例えば5-bitの値11110を組織符号化する場合を考える。まず、11110の末尾に10桁の0を追加して11110 00000 00000とする。次に、この15桁の値を多項式として生成多項式1 01001 10111で割ると、余りは00100 11101となる。最後に、11110 00000 00000から00100 11101を引くことで、求めたい符号語11110 00100 11101が得られる。
例2 (QRコードのVersion Informationで使われるBCH符号)
\(q=2, m=11\)の場合を考える。
\(\mathbb{F}_2\)係数の11次原始多項式\(f(x)=x^{11}+x^2+1\)を選択し、\(\mathbb{F}_{2^{11}}\)を構成する。また、\(\mathbb{F}_{2^{11}}\)の原始元を\(\alpha(x)=x\)とする。
\(2^{11}-1=23\times89\)なので\(n=23\)を選択し、\(\beta = \alpha^{89}\)とする。\(\beta\)の冪乗は次の表の通り。(計算過程は省略)
| 冪乗表記 | 2進表記 |
|---|---|
| 1 | 00000000001 |
| \(\beta^1=\alpha^{89}\) | 00101000010 |
| \(\beta^2=\alpha^{178}\) | 00010101110 |
| \(\beta^3=\alpha^{267}\) | 10010001100 |
| \(\beta^4=\alpha^{356}\) | 10001111100 |
| \(\beta^5=\alpha^{445}\) | 00111100001 |
| \(\beta^6=\alpha^{534}\) | 01001111101 |
| \(\beta^7=\alpha^{623}\) | 11110010110 |
| \(\beta^8=\alpha^{712}\) | 11101011111 |
| \(\beta^9=\alpha^{801}\) | 10111101110 |
| \(\beta^{10}=\alpha^{890}\) | 10010000011 |
| \(\beta^{11}=\alpha^{979}\) | 00010100111 |
| \(\beta^{12}=\alpha^{1068}\) | 11111011011 |
| \(\beta^{13}=\alpha^{1157}\) | 00110100010 |
| \(\beta^{14}=\alpha^{1246}\) | 00100011001 |
| \(\beta^{15}=\alpha^{1335}\) | 10111110101 |
| \(\beta^{16}=\alpha^{1424}\) | 00101111010 |
| \(\beta^{17}=\alpha^{1513}\) | 11011000000 |
| \(\beta^{18}=\alpha^{1602}\) | 11011010011 |
| \(\beta^{19}=\alpha^{1691}\) | 00100111111 |
| \(\beta^{20}=\alpha^{1780}\) | 01000101000 |
| \(\beta^{21}=\alpha^{1869}\) | 11101010100 |
| \(\beta^{22}=\alpha^{1958}\) | 10000111101 |
\(y^n-1 = y^{23}-1\)は次のように因数分解され、各因数に対して\(\beta\)の冪乗は表のように分類される。
\begin{align} y^{23} - 1 &= (y+1)(y^{11}+y^9+y^7+y^6+y^5+y+1)(y^{11}+y^{10}+y^6+y^5+y^4+y^2+1) \end{align}
| 多項式 | 根 |
|---|---|
| \(y+1\) | \(1\) |
| \(y^{11}+y^9+y^7+y^6+y^5+y+1\) | \(\beta, \beta^2, \beta^3, \beta^4, \beta^6, \beta^8, \beta^9, \beta^{12}, \beta^{13}, \beta^{16}, \beta^{18}\) |
| \(y^{11}+y^{10}+y^6+y^5+y^4+y^2+1\) | \(\beta^5, \beta^7, \beta^{10}, \beta^{11}, \beta^{14}, \beta^{15}, \beta^{17}, \beta^{19}, \beta^{20}, \beta^{21}, \beta^{22}\) |
生成多項式\(g(y)\)を
\begin{align} g(y) &= (y+1)(y^{11}+y^9+y^7+y^6+y^5+y+1) \\ &= y^{12}+y^{11}+y^{10}+y^9+y^8+y^5+y^2+1 \end{align}
と選択することで、\(g(y)\)には5つの連続する根\(1,\beta,\beta^2,\beta^3,\beta^4\)が含まれるる。したがって、このBCH符号の最小距離は6以上になる。また、\(g(y)\)は12次なので、このBCH符号は\((n,k)=(23,11)\)符号となる。
この12次の生成多項式では11-bitの元データを符号化することができるが、短縮符号を用いればより短い元データを符号化する際に符号語の長さも短縮することができる。
例えば6-bitの値100011を符号化する場合を考える。まず、100011の末尾に12桁の0を追加して100011 000000 000000とする。次に、この18桁の値を多項式として生成多項式1 111100 100101で割ると、余りは011110 011111となる。最後に、100011 000000 000000から011110 011111を引くことで、求めたい符号語100011 011110 011111が得られる。
このように\((n,k)=(23,11)\)符号を\((n,k)=(18,6)\)符号に短縮することができる。(同様の方法で\(k=1\)から\(k=10\)までの任意の長さに短縮することができ、短縮した分だけ符号語の長さも短くなる)
復号
BCH符号の復号(誤り訂正)には様々なアルゴリズムが存在するが、ここではPeterson法(PGZアルゴリズムとも呼ばれる)とForneyの公式について解説する。
誤り位置の特定
誤り位置を特定するアルゴリズムの一種であるPeterson法について解説する。
\(h=2t\)あるいは\(h=2t+1\)のBCH符号を考える。
符号語\(c(y)\)に誤り\(e(y)\)が加わって受信語\(r(y)=c(y)+e(y)\)に変化したとする。このとき、\(Hc=0\)であることから、シンドロームは\(s=He\in \mathbb{F}_{q^m}^h\)と計算できる。
誤りの個数が\(t\)個以下のとき、\(e(y)\)が\(L\leq t\)個の項\(j_1, j_2, \cdots, j_L\in \{0, 1, 2, \cdots, n-1\}\)で
\begin{align} e(y) = e_{j_1}y^{j_1} + \cdots + e_{j_L}y^{j_L} \end{align}
と表され、それ以外の項は0になっているものとする。(\(j_1, j_2, \cdots, j_L\)の中に0となるものが含まれていても良い)
このとき、シンドロームの各成分は具体的に
\begin{align} \left\{ \begin{array}{l} s_1 = e(\beta^a) = e_{j_1}\beta^{j_1a} + \cdots + e_{j_L}\beta^{j_La} \\ \:\vdots \\ s_i = e(\beta^{a+i-1}) = e_{j_1}\beta^{j_1(a+i-1)} + \cdots + e_{j_L}\beta^{j_L(a+i-1)} \\ \:\vdots \\ s_{2t} = e(\beta^{a+2t-1}) = e_{j_1}\beta^{j_1(a+2t-1)} + \cdots + e_{j_L}\beta^{j_L(a+2t-1)} \\ \end{array} \right. \end{align}
と表される。(\(h=2t+1\)の場合は\(s_{2t+1}\)の値も得られるが、いずれにしても訂正できる誤りの数は\(t\)個までなので\(s_{2t+1}\)は使わない)
\(\mathbb{F}_{q^m}\)係数の\(L\)次多項式\(\sigma(z)\)を次のように定義する。
\begin{align} \sigma(z) &:= (1-\beta^{j_1}z)(1-\beta^{j_2}z)\cdots(1-\beta^{j_L}z) \\ \end{align}
また、\(\sigma(z)\)を展開したときの各次の係数を\(\sigma_l\)とすると、次のようにも表せる。
\begin{align} \sigma(z) &:= (1-\beta^{j_1}z)(1-\beta^{j_2}z)\cdots(1-\beta^{j_L}z) \\ &= \sigma_Lz^L + \sigma_{L-1}z^{L-1} + \cdots + \sigma_1z + 1 \end{align}
この多項式\(\sigma(z)\)を誤り位置多項式と言う。
誤りを訂正する際、この段階では誤りが存在する位置の添字\(j_1, j_2, \cdots, j_L\in \{0, 1, 2, \cdots, n-1\}\)や、\(\sigma(z)\)の係数は具体的にはわかっていないのことに注意。
このとき、任意の\(1\leq l\leq L\)に対して\(\sigma(\beta^{-j_l})=0\)となるので、
\begin{align} \left\{ \begin{array}{l} 0 = \sigma_L\beta^{-Lj_1} + \sigma_{L-1}\beta^{-(L-1)j_1} + \cdots + \sigma_1\beta^{-j_1} + 1 \\ \:\vdots \\ 0 = \sigma_L\beta^{-Lj_l} + \sigma_{L-1}\beta^{-(L-1)j_l} + \cdots + \sigma_1\beta^{-j_l} + 1 \\ \:\vdots \\ 0 = \sigma_L\beta^{-Lj_L} + \sigma_{L-1}\beta^{-(L-1)j_L} + \cdots + \sigma_1\beta^{-j_L} + 1 \\ \end{array} \right. \end{align}
となる。
任意の\(i=0, 1, 2, \cdots, L-1\)を取り、上からそれぞれ\(e_{j_1}\beta^{(L+a+i)j_1}, \cdots, e_{j_l}\beta^{(L+a+i)j_l}, \cdots, e_{j_L}\beta^{(L+a+i)j_L}\)を掛けると次のようになる。
\begin{align} \left\{ \begin{array}{l} 0 = \sigma_Le_{j_1}\beta^{(a+i)j_1} + \sigma_{L-1}e_{j_1}\beta^{(a+i+1)j_1} + \cdots + \sigma_1e_{j_1}\beta^{(a+i+L-1)j_1} + e_{j_1}\beta^{(a+i+L)j_1} \\ \:\vdots \\ 0 = \sigma_Le_{j_l}\beta^{(a+i)j_l} + \sigma_{L-1}e_{j_l}\beta^{(a+i+1)j_l} + \cdots + \sigma_1e_{j_l}\beta^{(a+i+L-1)j_l} + e_{j_l}\beta^{(a+i+L)j_l} \\ \:\vdots \\ 0 = \sigma_Le_{j_L}\beta^{(a+i)j_L} + \sigma_{L-1}e_{j_L}\beta^{(a+i+1)j_L} + \cdots + \sigma_1e_{j_L}\beta^{(a+i+L-1)j_L} + e_{j_L}\beta^{(a+i+L)j_L} \\ \end{array} \right. \end{align}
これらの式を縦に足し合わせると、各項にシンドロームが出現する。
\begin{align} 0 = \sigma_Ls_{i+1} + \sigma_{L-1}s_{i+2} + \cdots + \sigma_1s_{i+L} + s_{i+L+1} \\ \end{align}
この関係は任意の\(i=0,1,2,\cdots,L-1\)に対して成り立つ。したがって、\(L\times L\)行列を用いて、
\begin{align} \begin{pmatrix} s_1 & s_2 & \cdots & s_L \\ s_2 & s_3 & \cdots & s_{L+1} \\ \vdots & \vdots & \ddots & \vdots \\ s_L & s_{L+1} & \cdots & s_{2L-1} \\ \end{pmatrix} \begin{pmatrix} \sigma_L \\ \sigma_{L-1} \\ \vdots \\ \sigma_1 \\ \end{pmatrix} = -\begin{pmatrix} s_{L+1} \\ s_{L+2} \\ \vdots \\ s_{2L} \\ \end{pmatrix} \end{align}
と表すことができる。この行列を\(S\)と表すことにする。
シンドロームは受信語と検査行列から計算できる値なので、誤りの位置が具体的にわかっていなくても計算することができる。
\(\det(S)\neq0\)ならば、\(S\)の逆行列を用いて、
\begin{align} \begin{pmatrix} \sigma_L \\ \sigma_{L-1} \\ \vdots \\ \sigma_1 \\ \end{pmatrix} = -S^{-1}\begin{pmatrix} s_{L+1} \\ s_{L+2} \\ \vdots \\ s_{2L} \\ \end{pmatrix} \end{align}
となるので、誤り位置多項式の係数を計算することができる。
こうして得られた誤り位置多項式に\(1, \beta^{-1}, \beta^{-2}, \cdots, \beta^{-(n-1)}\)を代入して0になる値を調べることで、\(L\)個の誤り位置\(j_1, j_2, \cdots, j_L\)を特定することができる。
\(S\)が逆行列を持つ条件を考える。
\(S\)はシンドロームだけで表すことができるが、一方
\begin{align} S &= \begin{pmatrix} s_1 & s_2 & \cdots & s_L \\ s_2 & s_3 & \cdots & s_{L+1} \\ \vdots & \vdots & \ddots & \vdots \\ s_L & s_{L+1} & \cdots & s_{2L-1} \\ \end{pmatrix} \\ &= \begin{pmatrix} 1 & 1 & \cdots & 1 \\ \beta^{j_1} & \beta^{j_2} & \cdots & \beta^{j_L} \\ \vdots & \vdots & \ddots & \vdots \\ \beta^{(L-1)j_1} & \beta^{(L-1)j_2} & \cdots & \beta^{(L-1)j_L} \\ \end{pmatrix} \begin{pmatrix} e_{j_1}\beta^{j_1a} & 0 & \cdots & 0 \\ 0 & e_{j_2}\beta^{j_2a} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & e_{j_L}\beta^{j_La} \\ \end{pmatrix} \begin{pmatrix} 1 & \beta^{j_1} & \cdots & \beta^{(L-1)j_1} \\ 1 & \beta^{j_2} & \cdots & \beta^{(L-1)j_2} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & \beta^{j_L} & \cdots & \beta^{(L-1)j_L} \\ \end{pmatrix} \\ \end{align}
という関係も成り立つ。
ここで、左右の行列は転置の関係にあり、左側を\(V\)と表す。これらの行列はVandermonde行列である。
中央の行列は対角行列であり、\(D:=\mathrm{diag}\left(e_{j_1}\beta^{j_1a}, e_{j_2}\beta^{j_2a}, \cdots, e_{j_L}\beta^{j_La}\right)\)と表すことにする。
\begin{align} S &= V \cdot \mathrm{diag}\left(e_{j_1}\beta^{j_1a}, e_{j_2}\beta^{j_2a}, \cdots, e_{j_L}\beta^{j_La}\right) \cdot V^\top \\ &= VDV^\top \end{align}
\(S\)の行列式を調べるとき、左右のVandermonde行列の行列式は0にはならないので、\(\det(S)=0\)となることと\(\det(D)=0\)となることは同値であるとわかる。
\(D\)の行列式は、
\begin{align} \det(D) &= \det \begin{pmatrix} e_{j_1}\beta^{j_1a} & 0 & \cdots & 0 \\ 0 & e_{j_2}\beta^{j_2a} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & e_{j_L}\beta^{j_La} \\ \end{pmatrix} \\ &= e_{j_1}\beta^{j_1a}e_{j_2}\beta^{j_2a}\cdots e_{j_L}\beta^{j_La} \\ &= e_{j_1}e_{j_2}\cdots e_{j_L}\beta^{j_1a}\beta^{j_2a}\cdots\beta^{j_La} \\ \end{align}
となる。
\(\beta^{j_la}\)は常に0以外の値を取るので、\(e_{j_1}e_{j_2}\cdots e_{j_L}=0\)ならば\(\det(S)=0\)で、その逆も成り立つと言える。
つまり、\(\det(S)=0\)ならば\(e_{j_1}e_{j_2}\cdots e_{j_L}=0\)となるので、\(e(y)\)の0ではない項の数は\(L-1\)個以下であることがわかる。その場合、最初に想定した\(e(y)\)の項の数\(L\)を1つ減らして、最初から同じ議論をやり直せば良い。
これらを踏まえて、\(2t\)以下の誤りがある場合には、次のようなアルゴリズムで誤りの個数\(L\)と位置\(j_1, j_2, \cdots, j_L\)を特定することができる。
- 検査行列\(H\)と受信語\(r\)を用いてシンドローム\(s=Hr\)を計算する。
- \(s=0\)ならば誤りがないと判定できる。\(s\neq0\)ならば3に進む。
- \(L=t\)とする。
- \(L\times L\)行列\(S\)を構成し、\(S\)の行列式を計算する。
- 行列式が0なら\(L\)を1減らして4に戻る。0でないなら6に進む。
- \(S\)の逆行列を用いて\(\sigma(z)\)の係数を得る。
- \(\sigma(z)\)に\(1, \beta^{-1}, \beta^{-2}, \cdots, \beta^{-(n-1)}\)を代入して0になる値を探し、\(L\)個の誤り位置\(j_1, j_2, \cdots, j_L\)を特定する。
誤り数値の特定
これまでの手順で誤り位置\(j_1, j_2, \cdots, j_L\)を特定できているので、
\begin{align} \begin{pmatrix} S_1 \\ S_2 \\ \vdots \\ S_L \end{pmatrix} &= \begin{pmatrix} \beta^{j_1a} & \beta^{j_2a} & \cdots & \beta^{j_La} \\ \beta^{j_1(a+1)} & \beta^{j_2(a+1)} & \cdots & \beta^{j_L(a+1)} \\ \vdots & \vdots & \ddots & \vdots \\ \beta^{j_1(a+L-1)} & \beta^{j_2(a+L-1)} & \cdots & \beta^{j_L(a+L-1)} \\ \end{pmatrix} \begin{pmatrix} e_{j_1} \\ e_{j_2} \\ \vdots \\ e_{j_L} \\ \end{pmatrix} \\ &= \begin{pmatrix} 1 & 1 & \cdots & 1 \\ \beta^{j_1} & \beta^{j_2} & \cdots & \beta^{j_L} \\ \vdots & \vdots & \ddots & \vdots \\ \beta^{j_1(L-1)} & \beta^{j_2(L-1)} & \cdots & \beta^{j_L(L-1)} \\ \end{pmatrix} \begin{pmatrix} \beta^{j_1a} & 0 & \cdots & 0 \\ 0 & \beta^{j_2a} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \beta^{j_La} \\ \end{pmatrix} \begin{pmatrix} e_{j_1} \\ e_{j_2} \\ \vdots \\ e_{j_L} \\ \end{pmatrix} \\ \end{align}
となることから逆行列を用いて誤り数値\(e_{j_1}, e_{j_2}, \cdots, e_{j_L}\)を求めることができる。(Vandermonde行列の行列式は0ではないので必ず逆行列が存在し、対角行列も各要素が\(\beta\)の冪乗なので行列式は0にはならず逆行列が存在する)
逆行列の計算を必要としない更に効率的な方法として、以下に紹介するForneyの公式というアルゴリズムも存在する。
まずシンドローム多項式を次のように定義する。
\begin{align} S(z) &:= \sum_{i=1}^h s_iz^{i-1} \\ &= s_hz^{h-1} + \cdots + s_2z + s_1 \end{align}
このとき、
\begin{align} S(z) &:= \sum_{i=1}^h s_iz^{i-1} \\ &= \sum_{i=1}^h \left(\sum_{l=1}^L e_{j_l}\beta^{j_l(a+i-1)}\right)z^{i-1} \\ &= \sum_{l=1}^L e_{j_l}\beta^{j_la} \sum_{i=1}^h \left(\beta^{j_l}z\right)^{i-1} \\ \end{align}
となる。
\(\sigma(z)=(1-\beta^{j_1}z)(1-\beta^{j_2}z)\cdots(1-\beta^{j_L}z)\)から\(1-\beta^{j_l}z\)を除いた多項式を\(\sigma_l(z)\)と表す。このとき、\(\sigma_l(z)\)は\(L-1\)次多項式であり、
\begin{align} \sigma(z) = (1-\beta^{j_l}z)\sigma_l(z) \end{align}
という関係を満たし、\(\sigma_l(z)\)に\(z=\beta^{-j_l}\)以外を代入すると\(\sigma_l(z)=0\)となる。
\(S(z)\sigma(z)\)は
\begin{align} S(z)\sigma(z) &= \sum_{l=1}^L e_{j_l}\beta^{j_la} \sigma(z) \sum_{i=1}^h \left(\beta^{j_l}z\right)^{i-1} \\ &= \sum_{l=1}^L e_{j_l}\beta^{j_la} \sigma_l(z)(1-\beta^{j_l}z) \sum_{i=1}^h \left(\beta^{j_l}z\right)^{i-1} \\ &= \sum_{l=1}^L e_{j_l}\beta^{j_la} \sigma_l(z)\left(1-\left(\beta^{j_l}z\right)^h\right) \\ \end{align}
となり、\(S(z)\sigma(z)\)を\(z^h\)で割った余りを\(\omega(z)\)とすると、
\begin{align} \omega(z) &= \sum_{l=1}^L e_{j_l}\beta^{j_la} \sigma_l(z) \\ \end{align}
と表せる。\(S(z)\)と\(\sigma(z)\)は既知なので、\(\omega(z)\)も受信語由来の値だけで具体的に係数を計算することができる。
\(\omega(z)\)に\(z=\beta^{-j_i}\)を代入すると、\(l=i\)の項だけが残り、
\begin{align} \omega(\beta^{-j_i}) &= e_{j_i}\beta^{j_ia} \sigma_i(\beta^{-j_i}) \\ \end{align}
となる。
次に、\(\sigma(z)\)に対する形式微分を行う。
多項式
\begin{align} f(x) = f_nx^n + \cdots f_1x + f_0 \end{align}
に対して
\begin{align} f'(x) := nf_nx^{n-1} + \cdots + 2f_2x + f_1 \end{align}
と定義される多項式を\(f\)の形式微分と言う。
2つの多項式\(f(x), g(x)\)と係数\(a,b\)に対して
\begin{align} (af+bg)'(x) &= n(af_n+bg_n)x^{n-1} + \cdots + 2(af_2+bg_2)x + af_1+bg_1 \\ &= a\left(nf_nx^{n-1} + \cdots + 2f_2x + f_1\right) + b\left(ng_nx^{n-1} + \cdots + 2g_2x + g_1\right) \\ &= af'(x) + bg'(x) \\ \end{align}
となることから、形式微分には線形性があると言える。
(上の式では\(f,g\)で大きい方の次数を\(n\)とし、次数の小さい方の高次の係数を0としている)
また、
\begin{align} (x^mf)'(x) &= (m+n)f_nx^{m+n-1} + \cdots + (m+2)f_2z^{m+1} + (m+1)f_1x^m + mf_0x^{m-1} \\ &= mx^{m-1}\left(f_nx^n + \cdots + f_1x + f_0\right) + x^m\left(nf_nx^{n-1} + \cdots + 2f_2x + f_1\right) \\ &= (x^m)'f(x) + x^mf'(x) \\ \end{align}
となり、既に示した線形性と組み合わせることでLeibniz則
\begin{align} (g(x)f(x))' = g'(x)f(x) + g(x)f'(x) \end{align}
が成り立つことがわかる。
このようにして形式的な多項式に対しても微分を定義することができる。形式微分は元の多項式の係数さえわかっていれば計算可能である。(今回は\(\sigma(z)\)の係数を既に得ているので\(\sigma'(z)\)を計算することができる)
\(\sigma(z) = (1-\beta^{j_1}z)(1-\beta^{j_2}z)\cdots(1-\beta^{j_L}z)\)にLeibniz則を適用して微分すると
\begin{array}{lll} \sigma'(z) &=& -\beta^{j_1}(1-\beta^{j_2}z)\cdots(1-\beta^{j_L}z) \\ && -\beta^{j_2}(1-\beta^{j_1}z)\cdots(1-\beta^{j_L}z) \\ && \:\vdots \\ && -\beta^{j_L}(1-\beta^{j_1}z)\cdots(1-\beta^{j_{L-1}}z) \\ &=& -\beta^{j_1}\sigma_1(z) -\beta^{j_2}\sigma_2(z) - \cdots -\beta^{j_L}\sigma_L(z) \\ \end{array}
となり、こちらも\(x=\beta^{-j_i}\)を代入すると\(l=i\)の項だけが残って
\begin{align} \sigma'(\beta^{-j_i}) &= -\beta^{j_i}\sigma_i(\beta^{-j_i}) \end{align}
となる。
したがって、\(\omega(\beta^{-j_i})\)の式と\(\sigma'(\beta^{-j_i})\)の式に共通する\(\sigma_i(\beta^{-j_i})\)を消去することで、
\begin{align} e_{j_i} = -\frac{\omega(\beta^{-j_i})}{\sigma'(\beta^{-j_i})\beta^{(a-1)j_i}} \end{align}
と誤り数値を計算することができる。
- シンドローム\(s\)の値を係数とするシンドローム多項式\(S(z)\)を作る。
- シンドローム多項式\(S(z)\)と誤り位置多項式\(\sigma(z)\)の積を\(z^h\)で割った余りを\(\omega(z)\)とする。
- \(\sigma(z)\)の形式微分\(\sigma'(z)\)を求める。
- それぞれの位置の誤り数値を\(e_{j_i} = -\frac{\omega(\beta^{-j_i})}{\sigma'(\beta^{-j_i})\beta^{(a-1)j_i}}\)によって求める。
RS符号
RS符号(Reed-Solomon符号)は、1960年にReedとSolomonによって考案された符号で、BCH符号の一種。
BCH符号(の\(q=2\)の場合)がビット単位の誤り訂正に適しているのに対し、RS符号はシンボル(=複数ビット)単位で誤りを訂正する能力を持つ。このため、バースト誤り(=連続するビット誤り)を一括して1つのシンボル誤りとして処理できる点が大きな利点である。
また、一般のBCH符号と比べて訂正能力と符号長の関係が明快で構成も簡潔であるという特徴を持つ。
RS符号は次のような幅広い分野で活用されている。
- CD・DVD・BD
- 地上デジタル放送
- 衛星通信
- ADSL
- RAID 6の第2パリティ
- RAR形式のファイル圧縮
- QRコード
符号化
RS符号は、BCH符号において\(m=1\)とした特殊な場合である。
位数\(q\)の有限体\(\mathbb{F}_q\)を取り、符号長\(n\)を\(n=q-1\)とする。(符号\(C\)は\(\mathbb{F}_q^n\)の部分空間)
\(\mathbb{F}_q\)の原始元\(\alpha\)とすると、
\begin{align} \mathbb{F}_q &= \left\{0, 1, \alpha, \alpha^2, \cdots, \alpha^{n-1}\right\} \\ \end{align}
となる。
\(\mathbb{F}_q\)の0以外の全ての要素は\(y^n-1\)の根となるので、\(y^n-1\)は次のようにわかりやすく因数分解される。
\begin{align} y^n-1 = (y-1)(y-\alpha)(y-\alpha^2)\cdots(y-\alpha^{n-1}) \end{align}
ここから\(\alpha\)の指数が連続する因数を選択することは非常に容易で、\(n-k\leq n\)に対して
\begin{align} g(y) = (y-1)(y-\alpha)(y-\alpha^2)\cdots(y-\alpha^{n-k-1}) \end{align}
とすれば良い。
検査行列\(H\)もBCH符号と同様にVandermonde行列として実装する。
(このとき、符号語は\(\mathbb{F}_q\)値ベクトルであり、\(H\)も符号語と同じ\(\mathbb{F}_q\)値の行列となる)
\begin{align} H = \begin{pmatrix} 1 & 1 & \cdots & 1 & 1 & 1 \\ \alpha^{n-1} & \alpha^{n-2} & \cdots & \alpha^{2} & \alpha & 1 \\ \alpha^{(n-1)\cdot2} & \alpha^{(n-2)\cdot2} & \cdots & \alpha^{4} & \alpha^{2} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ \alpha^{(n-1)(n-k-1)} & \alpha^{(n-2)(n-k-1)} & \cdots & \alpha^{2(n-k-1)} & \alpha^{n-k-1} & 1 \end{pmatrix} \end{align}
BCH符号の性質からこの符号の最小距離は\(n-k+1\)以上である。一方、\(g(y)\)自体も符号語であり、その次数は\(n-k\)なので\(g(y)\)の重みは\(n-k+1\)以下となる。よって最小距離はちょうど\(n-k+1\)となる。
このことから、RS符号は\((n,k,n-k+1)\)符号であり、最小距離を符号長と元データの長さによって簡潔に表現することができる。
RS符号の符号長\(n=q-1\)は有限体の要素数にほぼ等しいので符号語が非常に長くなる場合があるが、実際には短縮符号を用いて利用されることが多い。
例
\(q=2^8\)の場合を考える。
\(\mathbb{F}_{2^8}=\mathbb{F}_2[x]/(x^8+x^4+x^3+x^2+1)\)としたとき、原始元\(\alpha\)の冪乗は次のようになる。(最初の一部だけ掲載)
| 冪乗表記 | 2進表記 |
|---|---|
| 1 | 00000001 |
| \(\alpha^1\) | 00000010 |
| \(\alpha^2\) | 00000100 |
| \(\alpha^3\) | 00001000 |
| \(\alpha^4\) | 00010000 |
| \(\alpha^5\) | 00100000 |
| \(\alpha^6\) | 01000000 |
| \(\alpha^7\) | 10000000 |
| \(\alpha^8\) | 00011101 |
| \(\alpha^9\) | 00111010 |
| \(\alpha^{10}\) | 01110100 |
| \(\alpha^{11}\) | 11101000 |
| \(\alpha^{12}\) | 11001101 |
| \(\alpha^{13}\) | 10000111 |
| \(\alpha^{14}\) | 00010011 |
| \(\alpha^{15}\) | 00100110 |
| \(\alpha^{16}\) | 01001100 |
| \(\alpha^{17}\) | 10011000 |
| \(\alpha^{18}\) | 00101101 |
| \(\alpha^{19}\) | 01011010 |
| \(\alpha^{20}\) | 10110100 |
| \(\alpha^{21}\) | 01110101 |
\(n-k=22\)とすると生成多項式は次のようになる。(計算過程は省略)
\begin{align} g(y) &= (y-\alpha^0)(y-\alpha^1)(y-\alpha^2)\cdots (y-\alpha^{21}) \\ &= y^{22} + \alpha^{210}y^{21} + \alpha^{171}y^{20} + \alpha^{247}y^{19} + \alpha^{242}y^{18} + \alpha^{93}y^{17} + \alpha^{230}y^{16} + \alpha^{14}y^{15} + \alpha^{109}y^{14} + \alpha^{221}y^{13} + \alpha^{53}y^{12} + \alpha^{200}y^{11} + \alpha^{74}y^{10} + \alpha^{8}y^9 + \alpha^{172}y^8 + \alpha^{98}y^7 + \alpha^{80}y^6 + \alpha^{219}y^5 + \alpha^{134}y^4 + \alpha^{160}y^3 + \alpha^{105}y^2 + \alpha^{165}y + \alpha^{231} \\ \end{align}
このRS符号は\((n,k,d)=(255,233,23)\)符号となる。
(実際には短縮符号として例えば\((n,k,d)=(34,12,23)\)のように利用する)
復号
RS符号はBCH符号の特殊な場合なので、BCH符号の復号方法をそのまま適用できる。