球面調和関数
この投稿では3次元Laplace方程式
\begin{align} 0 = \Delta\psi(x,y,z) \end{align}
について考え、球面調和関数を導出する。
球面調和関数は量子力学において水素原子の波動関数を求める際に現れる他、電磁気学や流体力学でも扱われることがあるらしい。また、(Fourier級数展開のように)球面調和関数が球面上の任意の関数を近似できるという性質に着目して、3Dグラフィックの分野では見る方向に依存した色の変化を表現するために利用されている。
目次
Laplace方程式の変数分離解
Laplace方程式
次のように定義される偏微分方程式をLaplace方程式といい、その解は調和関数(harmonic function)と呼ばれる。
\begin{align} 0 &= \Delta\psi(x,y,z) \\ &= \partial_x^2\psi(x,y,z) + \partial_y^2\psi(x,y,z) + \partial_z^2\psi(x,y,z) \end{align}
ここではその特殊解を探していく。
変数分離法
Laplace方程式はLaplace演算子の極座標表示により
\begin{align} 0 &= \Delta\psi(x,y,z) \\ &= \frac{1}{r^2} \left( \partial_r(r^2\partial_r) + \frac{1}{\sin\theta}\partial_\theta(\sin\theta\partial_\theta) + \frac{1}{(\sin\theta)^2}\partial_\phi^2 \right)\psi(x,y,z) \end{align}
と表すことができ、両辺に\(r^2\)を掛けると
\begin{align} 0 &= \left( \partial_r(r^2\partial_r) + \frac{1}{\sin\theta}\partial_\theta(\sin\theta\partial_\theta) + \frac{1}{(\sin\theta)^2}\partial_\phi^2 \right)\psi(x,y,z) \end{align}
となる。
ここで\(\psi\)に次のような仮定を課す。
\begin{align} \psi(x,y,z) = R(r)\Theta(\theta)\Phi(\phi) \end{align}
このようにして微分方程式の特殊解を求める方法を変数分離法という。
これを方程式に代入すると、
\begin{align} 0 &= \left( \partial_r(r^2\partial_r) + \frac{1}{\sin\theta}\partial_\theta(\sin\theta\partial_\theta) + \frac{1}{(\sin\theta)^2}\partial_\phi^2 \right)\left(R(r)\Theta(\theta)\Phi(\phi)\right) \\ &= \Theta(\theta)\Phi(\phi)\partial_r(r^2\partial_rR(r)) + R(r)\left(\Phi(\phi)\frac{1}{\sin\theta}\partial_\theta(\sin\theta\partial_\theta\Theta(\theta)) + \frac{\Theta(\theta)}{(\sin\theta)^2}\partial_\phi^2\Phi(\phi) \right) \\ &= R(r)\Theta(\theta)\Phi(\phi) \left(\frac{1}{R(r)}\partial_r(r^2\partial_rR(r)) + \frac{1}{(\sin\theta)^2}\left(\frac{\sin\theta}{\Theta(\theta)}\partial_\theta(\sin\theta\partial_\theta\Theta(\theta)) + \frac{1}{\Phi(\phi)}\partial_\phi^2\Phi(\phi) \right) \right) \\ \end{align}
両辺を\(R(r)\Theta(\theta)\Phi(\phi)\)で割ると、
\begin{align} 0 &= \frac{1}{R(r)}\partial_r(r^2\partial_rR(r)) + \frac{1}{(\sin\theta)^2}\left(\frac{\sin\theta}{\Theta(\theta)}\partial_\theta(\sin\theta\partial_\theta\Theta(\theta)) + \frac{1}{\Phi(\phi)}\partial_\phi^2\Phi(\phi) \right) \\ \end{align}
つまり、
\begin{align} \frac{1}{R(r)}\partial_r(r^2\partial_rR(r)) &= -\frac{1}{(\sin\theta)^2}\left(\frac{\sin\theta}{\Theta(\theta)}\partial_\theta(\sin\theta\partial_\theta\Theta(\theta)) + \frac{1}{\Phi(\phi)}\partial_\phi^2\Phi(\phi) \right) \\ \end{align}
となる。
変数\(r\)に関して見ると右辺は定数、変数\(\theta,\phi\)に関して見ると左辺もまた定数なので、\(r,\theta,\phi\)のいずれにも依存しない定数\(\lambda\)を用いて、
\begin{align} \lambda &= \frac{1}{R(r)}\partial_r(r^2\partial_rR(r)) \\ \lambda &= -\frac{1}{(\sin\theta)^2}\left(\frac{\sin\theta}{\Theta(\theta)}\partial_\theta(\sin\theta\partial_\theta\Theta(\theta)) + \frac{1}{\Phi(\phi)}\partial_\phi^2\Phi(\phi) \right) \end{align}
という関係が成り立つと言える。
また、2つ目の式からは更に、
\begin{align} \frac{\sin\theta}{\Theta(\theta)}\partial_\theta(\sin\theta\partial_\theta\Theta(\theta)) + \lambda(\sin\theta)^2 &= -\frac{1}{\Phi(\phi)}\partial_\phi^2\Phi(\phi) \end{align}
という関係を導くことができ、この式もまた左辺は\(\phi\)に対して定数、右辺は\(\theta\)に対して定数なので、共通の定数\(\nu\)を用いて
\begin{align} \nu &= \frac{\sin\theta}{\Theta(\theta)}\partial_\theta(\sin\theta\partial_\theta\Theta(\theta)) + \lambda(\sin\theta)^2 \\ \nu &= -\frac{1}{\Phi(\phi)}\partial_\phi^2\Phi(\phi) \end{align}
という関係が成り立つことがわかる。
Laplace方程式
\begin{align} 0 = \Delta\psi(x,y,z) \end{align}
の特殊解\(\psi(x,y,z)=R(r)\Theta(\theta)\Phi(\phi)\)は次の方程式を満たさなければならない。
\begin{align} \lambda &= \frac{1}{R(r)}\partial_r(r^2\partial_rR(r)) \\ \nu &= \frac{\sin\theta}{\Theta(\theta)}\partial_\theta(\sin\theta\partial_\theta\Theta(\theta)) + \lambda(\sin\theta)^2 \\ \nu &= -\frac{1}{\Phi(\phi)}\partial_\phi^2\Phi(\phi) \end{align}
Rの解
\(R(r)\)の解を求める。
\begin{align} \lambda &= \frac{1}{R(r)}\partial_r(r^2\partial_rR(r)) \end{align}
より、
\begin{align} \lambda R(r) = \partial_r(r^2\partial_rR(r)) \end{align}
となるが、これは2階斉次常微分方程式なので、2つの特殊解を見つけるだけで一般解を線形結合で表現することができる。
\(R(r) = r^l\)としてみると、
\begin{align} \lambda R(r) &= \partial_r(r^2\partial_rR(r)) \\ &= \partial_r(r^2\partial_rr^l) \\ &= \partial_r(lr^{l+1}) \\ &= l(l+1)r^l \\ &= l(l+1)R(r) \end{align}
となるので、\(\lambda = l(l+1)\)ならば\(R(r)=r^l\)は特殊解になる。
\(\lambda > -\frac{1}{4}\)のとき、そのような\(l\)は
\begin{align} l = -\frac{1\pm\sqrt{2\lambda+1}}{2} \end{align}
と表すことができ、片方を\(l\)とするともう片方は\(-l-1\)である。
\(\lambda > -\frac{1}{4}\)のとき、\(R(r)=r^l\)と\(R(r)=r^{-1-l}\)は線形独立した2つの特殊解となり、一般解は
\begin{align} R(r) = ar^l + br^{-1-l} \end{align}
と表すことができる。
\(\lambda > -\frac{1}{4}\)のとき、\(\lambda = l(l+1)\)を満たす\(l>-\frac{1}{2}\)に対して、
\begin{align} R(r) = ar^l + br^{-1-l} \end{align}
と表すことができる。(\(a, b\)は定数)
Φの解
\(\Phi(\phi)\)の解を求める。
\begin{align} \nu &= -\frac{1}{\Phi(\phi)}\partial_\phi^2\Phi(\phi) \end{align}
より、
\begin{align} \partial_\phi^2\Phi(\phi) = -\nu\Phi(\phi) \end{align}
となる。
ここで、\(m:=\sqrt{|\nu|}\)と置く。
\(\nu < 0 \)のとき、\(e^{m\phi}, e^{-m\phi}\)が線形独立な特殊解となる。
しかし、\(\Phi(\phi)\)はそもそも周期性を持つという制約があるので、これらの解は適さない。
\(\nu > 0 \)のとき、\(\sin(m\phi), \cos(m\phi)\)が線形独立な特殊解となる。(複素数値なら\(e^{im\phi}, e^{-im\phi}\)としても良い)
このときもまた周期が\(2\pi\)という制約を満たさなければならないので、\(m\)は整数でなければならない。
一般解は
\begin{align} \Phi(\phi) = a\sin(m\phi) + b\cos(m\phi) \end{align}
と表すことができる。
非負の整数\(m\)に対して\(\nu=m^2\)となるとき、
\begin{align} \Phi(\phi) = a\sin(m\phi) + b\cos(m\phi) \end{align}
と表すことができる。(\(a, b\)は定数)
Θの解
\(\Theta(\theta)\)の解を求める。
\begin{align} \nu &= \frac{\sin\theta}{\Theta(\theta)}\partial_\theta(\sin\theta\partial_\theta\Theta(\theta)) + \lambda(\sin\theta)^2 \\ \end{align}
より、
\begin{align} m^2\Theta(\theta) &= \sin\theta\partial_\theta(\sin\theta\partial_\theta\Theta(\theta)) + l(l+1)(\sin\theta)^2\Theta(\theta) \\ \end{align}
となる。
ここで、\(w=\cos\theta=\frac{z}{r}\in[-1,1]\)とすると、
\begin{align} \sin\theta\partial_\theta &= \sin\theta\frac{dw}{d\theta}\frac{d}{dw} \\ &= -(\sin\theta)^2\frac{d}{dw} \\ &= -(1-w^2)\frac{d}{dw} \\ \end{align}
となるので、
\begin{align} m^2\Theta(\theta) &= \sin\theta\partial_\theta(\sin\theta\partial_\theta\Theta(\theta)) + l(l+1)(\sin\theta)^2\Theta(\theta) \\ &= (1-w^2)\frac{d}{dw}\left((1-w^2)\frac{d}{dw}\Theta(\theta)\right) + l(l+1)(1-w^2)\Theta(\theta) \\ \end{align}
となって、Legendreの陪方程式(Associated Legendre Equation, General Legendre Equation)と呼ばれる次の方程式が得られる。
\begin{align} 0 &= \frac{d}{dw}\left((1-w^2)\frac{d}{dw}\Theta(\theta)\right) + \left( l(l+1) - \frac{m^2}{(1-w^2)} \right)\Theta(\theta) \\ \end{align}
Legendreの陪方程式の(非特異な)解は、Legendre陪多項式となる。
\begin{align} \Theta(\theta(w)) \propto P_l^m(w) &= (1-w^2)^{m/2}\left(\frac{d}{dw}\right)^mP_l(w) \\ &= (1-w^2)^{m/2}\left(\frac{d}{dw}\right)^{l+m}(w^2-1)^l \end{align}
\(w=\cos(\theta)\)とする。非負の整数\(l, m\)に対して、
\begin{align} \Theta(\theta) = aP_l^m(w) &= a(1-w^2)^{m/2}\left(\frac{d}{dw}\right)^mP_l(w) \\ &= a(1-w^2)^{m/2}\left(\frac{d}{dw}\right)^{l+m}(w^2-1)^l \end{align}
と表すことができる。(\(a\)は定数)
なお、\(m>l\)のとき、\(\Theta(\theta)=0\)となる。
球面調和関数
これまでの結果をまとめると、Laplace方程式\(0=\Delta \psi(x,y,z)\)の極座標における変数分離解
\begin{align} \psi(x,y,z) = R(r)\Theta(\theta)\Phi(\phi) \end{align}
は、
\begin{align} R(r) &= c_1r^l + c_2r^{-1-l} \\ \Theta(\theta) &= c_3P_l^m(\cos(\theta)) \\ \Phi(\phi) &= c_4\sin(m\phi) + c_5\cos(m\phi) \end{align}
で表されることがわかった。(\(l,m\)は\(0\leq m\leq l\)を満たす整数)
ここでは調和関数の球面上での性質を調べるため、\(r\)を固定して定数とする。
つまり、球面調和関数\(Y_{l,m}(\theta,\phi) = \Theta(\theta)\Phi(\phi)\)に関して調べる。
正規直交性
(実)関数空間\(L^2(\Omega)\)の可算部分集合\(\{e_n\}_{n=0}^\infty\)が正規直交系であるとは、
\begin{align} \langle e_n, e_{n'} \rangle_{L^2(\Omega)} = \delta_{n,n'} \\ \end{align}
つまり、
\begin{align} \int_\Omega e_n(x)e_{n'}(x)dx = \delta_{n,n'} \\ \end{align}
となることである。
\(Y_{l,m}\)が\(L^2(S^2)\)の正規直交系となるように以下のように調整する。(\(S^2\)は単位球面)
Φの正規直交性
\(\Phi(\phi)\)の正規直交系を構成するため、\(m\)を整数全体に拡張して、
\begin{align} \Phi_m(\phi) := \begin{cases} \frac{1}{\sqrt{\pi}}\cos(m\phi) &\qquad (m>0) \\ \frac{1}{\sqrt{2\pi}} &\qquad (m=0) \\ \frac{1}{\sqrt{\pi}}\sin(-m\phi) &\qquad (m<0) \\ \end{cases} \end{align}
とする。
これはFourier級数展開でもよく知られているように、\(L^2([0,2\pi))\)の正規直交基底である。
実際に、
\begin{align} \int_0^{2\pi} \frac{1}{\sqrt{\pi}}\cos(m\phi)\frac{1}{\sqrt{\pi}}\cos(m'\phi) d\phi &= \frac{1}{\pi}\int_0^{2\pi} \cos(m\phi)\cos(m'\phi) d\phi \\ &= \frac{1}{2\pi}\int_0^{2\pi} \left(\cos((m+m')\phi) + \cos((m-m')\phi)\right) d\phi \\ \end{align}
であるが、\(m\neq m'\)のときは、
\begin{align} \int_0^{2\pi} \frac{1}{\sqrt{\pi}}\cos(m\phi)\frac{1}{\sqrt{\pi}}\cos(m'\phi) d\phi &= \frac{1}{2\pi}\int_0^{2\pi} \left(\cos((m+m')\phi) + \cos((m-m')\phi)\right) d\phi \\ &= \frac{1}{2\pi} \left[ \frac{1}{m+m'}\sin((m+m')\phi) + \frac{1}{m-m'}\sin((m-m')\phi)\right]_0^{2\pi} \\ &= 0 \\ \end{align}
\(m=m'\)のときは、
\begin{align} \int_0^{2\pi} \frac{1}{\sqrt{\pi}}\cos(m\phi)\frac{1}{\sqrt{\pi}}\cos(m'\phi) d\phi &= \frac{1}{2\pi}\int_0^{2\pi} \left(\cos((m+m')\phi) + \cos((m-m')\phi)\right) d\phi \\ &= \frac{1}{2\pi}\int_0^{2\pi} \left(\cos(2m\phi) + 1\right) d\phi \\ &= \frac{1}{2\pi} \left[ \frac{1}{2m}\sin(2m\phi) + \phi \right]_0^{2\pi} \\ &= \frac{1}{2\pi} \left( 0 + 2\pi \right) \\ &= 1 \\ \end{align}
となる。
また、
\begin{align} \int_0^{2\pi} \frac{1}{\sqrt{2\pi}}\frac{1}{\sqrt{\pi}}\cos(m\phi) d\phi &= \frac{1}{\sqrt{2}\pi}\int_0^{2\pi} \cos(m\phi) d\phi \\ &= \frac{1}{\sqrt{2}\pi} \left[\frac{1}{m}\cos(m\phi)\right]_0^{2\pi} \\ &= 0 \\ \end{align}
これら3つは\(\sin\)についても同様。
更に、
\begin{align} \int_0^{2\pi} \frac{1}{\sqrt{\pi}}\sin(m\phi)\frac{1}{\sqrt{\pi}}\cos(m'\phi) d\phi &= \frac{1}{\pi}\int_0^{2\pi} \sin(m\phi)\cos(m'\phi) d\phi \\ &= \frac{1}{\pi}\int_{-\pi}^\pi \sin(m\phi)\cos(m'\phi) d\phi \\ \end{align}
は積分の中が奇関数なので0。
最後に、
\begin{align} \int_0^{2\pi} \frac{1}{\sqrt{2\pi}}\frac{1}{\sqrt{2\pi}} d\phi &= \frac{1}{2\pi}\int_0^{2\pi} d\phi \\ &= 1 \\ \end{align}
となるので、確かにこれは正規直交系である。
Θの正規直交性
\(\Theta_{l,m}(\theta)\)も(\(l\)に関して)正規直交基底となるように係数を調整する。
Legendre陪多項式の性質によると、
\begin{align} \int_{-1}^1P_l^m(x)P_{l'}^m(x)dx &= \frac{2(l+m)!}{(2l+1)(l-m)!}\delta_{l,l'} \\ \end{align}
なので、
\begin{align} \Theta_{l,m}(\theta) &= \sqrt{\frac{(2l+1)(l-m)!}{2(l+m)!}}P_l^m(\cos(\theta)) \\ \end{align}
とすれば、\(\int_0^\pi\cdot\sin(\theta)d\theta\)によって定義される内積に関して正規直交系になる。
\(\Phi\)で\(m\)を整数全体に拡張したことと合わせるため、\(\Theta_{l,-m}(\theta) = \Theta_{l,m}(\theta)\)とする。
Yの正規直交性
\(Y_{l,m}(\theta,\phi)\)は次のようになる。
\begin{align} Y_{l,m}(\theta,\phi) &= \Theta_{l,m}(\theta)\Phi_m(\phi) = \begin{cases} \sqrt{\frac{(2l+1)(l-m)!}{2\pi(l+m)!}}P_l^m(\cos(\theta))\cos(m\phi) &\qquad (m>0) \\ \sqrt{\frac{2l+1}{4\pi}}P_l(\cos(\theta)) &\qquad (m=0) \\ \sqrt{\frac{(2l+1)(l-|m|)!}{2\pi(l+|m|)!}}P_l^{|m|}(\cos(\theta))\sin(|m|\phi) &\qquad (m<0) \\ \end{cases} \end{align}
球面全体の積分に対して、
\begin{align} \int_{S^2} Y_{l,m}(\theta,\phi)Y_{l',m'}(\theta,\phi) d\Omega &= \int_0^\pi \int_0^{2\pi} Y_{l,m}(\theta,\phi)Y_{l',m'}(\theta,\phi) \sin(\theta) d\phi d\theta \\ &= \int_0^\pi \Theta_{l,m}(\theta)\Theta_{l',m'}(\theta) \sin(\theta) d\theta \int_0^{2\pi} \Phi_m(\phi)\Phi_{m'}(\phi) d\phi \\ &= \int_0^\pi \Theta_{l,m}(\theta)\Theta_{l',m'}(\theta) \sin(\theta) d\theta \delta_{m,m'} \\ &= \delta_{l,l'} \delta_{m,m'} \\ \end{align}
が成り立つ。
完全性
(実)関数空間\(L^2(\Omega)\)の可算部分集合\(\{e_n\}_{n=0}^\infty\)が完全系であるとは、\(\{e_n\}_{n=0}^\infty\)が張る空間(=\(\{e_n\}_{n=0}^\infty\)の有限個の線形結合全体の空間)が、\(L^2(\Omega)\)で稠密になっていることを言う。
言い換えれば、任意の\(f\in L^2(\Omega)\)に対して、任意の精度\(\varepsilon>0\)で有限個の線形結合が\(f\)を近似できるということである。
\begin{align} \left\| f - \sum_{n=0}^N c_n e_n \right\|_{L^2(\Omega)} < \varepsilon \end{align}
このとき選ばれる\(\{c_n\}_{n=0}^N\)は\(\varepsilon\)に依存していることに注意。
ここで、L2ノルムは
\begin{align} \left\| f \right\|_{L^2(\Omega)} := \left(\int_\Omega f(x)^2 dx\right)^{1/2} \end{align}
と定義される。
\(\{e_n\}_{n=0}^\infty\)が更に正規直交系でもあるならば、\(e_R := f - \sum_{n=0}^N\left\langle f,e_n \right\rangle e_n\)と置くと、
\begin{align} \left\langle e_R, e_n \right\rangle &= \left\langle f - \sum_{n'=0}^N\left\langle f,e_{n'} \right\rangle e_n', e_n \right\rangle \\ &= \left\langle f, e_n \right\rangle - \left\langle \sum_{n'=0}^N \left\langle f,e_{n'} \right\rangle e_{n'}, e_n \right\rangle \\ &= \left\langle f, e_n \right\rangle - \sum_{n'=0}^N \left\langle f,e_{n'} \right\rangle \left\langle e_{n'}, e_n \right\rangle \\ &= \left\langle f, e_n \right\rangle - \sum_{n'=0}^N \left\langle f,e_{n'} \right\rangle \delta_{n,n'} \\ &= \left\langle f, e_n \right\rangle - \left\langle f,e_n \right\rangle \\ &= 0 \\ \end{align}
となり、任意の\(e_n\)と\(e_R\)は直交している。また、\(\{e_n\}_{n=0}^N\)同士も当然直交しているので、\(\{e_0,e_1,e_2,\cdots,e_{N-1},e_N,e_R\}\)は直交系である。
したがって、任意の\(\{a_n\}_{n=0}^N\cup\{a_R\}\subset \mathbb{R}\)に対して、
\begin{align} \left\| a_Re_R + \sum_{n=0}^Na_ne_n \right\|^2 &= \left\langle a_Re_R + \sum_{n=0}^Na_ne_n, a_Re_R + \sum_{n=0}^Na_ne_n \right\rangle \\ &= a_R^2\|e_R\|^2 + \sum_{n=0}^N a_n^2\|e_n\|^2 \\ &= a_R^2\|e_R\|^2 + \sum_{n=0}^N a_n^2 \\ \end{align}
が成り立つ。(三平方の定理)
このことを利用すると、
\begin{align} \varepsilon^2 &> \left\| f - \sum_{n=0}^Nc_ne_n \right\|^2 \\ &= \left\| f - \sum_{n=0}^N\left\langle f,e_n \right\rangle e_n + \sum_{n=0}^N\left\langle f,e_n \right\rangle e_n - \sum_{n=0}^Nc_ne_n \right\|^2 \\ &= \left\| e_R + \sum_{n=0}^N\left(\left\langle f,e_n \right\rangle - c_n\right)e_n \right\|^2 \\ &= \left\|e_R\right\|^2 + \sum_{n=0}^N\left(\left\langle f,e_n \right\rangle - c_n\right)^2 \\ &\geq \left\|e_R\right\|^2 \\ &= \left\| f - \sum_{n=0}^N\left\langle f,e_n \right\rangle e_n \right\|^2 \end{align}
となって、\(c_n\)の具体例として\(c_n=\left\langle f,e_n\right\rangle\)が完全性の式を満たすことがわかる。
したがって、完全性の関係は次のように表すこともできる。
\begin{align} f = \sum_{n=0}^\infty \left\langle f, e_n \right\rangle e_n \end{align}
なお、完全系が特に線形独立であるとき、その完全系を基底と呼ぶ。
完全正規直交系は線形独立なので、正規直交基底と呼ぶこともできる。
Parsevalの等式
\(\{e_n\}_{n=0}^\infty\)が完全正規直交系であるとき、
\begin{align} \left| \|f\|^2 - \sum_{n=0}^N \left\langle f,e_n \right\rangle^2 \right| &= \left| \|f\|^2 - \left\| \sum_{n=0}^N \left\langle f,e_n \right\rangle e_n\right\|^2 \right| \\ &= \left\|f - \sum_{n=0}^N \left\langle f,e_n \right\rangle e_n\right\|^2 \\ &< \varepsilon^2 \end{align}
なので、次の等式が成り立つ。この等式をParsevalの等式と言う。
\begin{align} \|f\|^2 = \sum_{n=0}^\infty \left\langle f,e_n \right\rangle^2 \end{align}
逆に正規直交系でParsevalの等式が成り立つとき、
\begin{align} \left\| f - \sum_{n=0}^N \left\langle f,e_n \right\rangle e_n \right\|^2 &= \left\|f\right\|^2 - 2\left\langle f, \sum_{n=0}^N \left\langle f,e_n \right\rangle e_n \right\rangle + \left\langle \sum_{n=0}^N \left\langle f,e_n \right\rangle e_n, \sum_{n=0}^N \left\langle f,e_n \right\rangle e_n \right\rangle \\ &= \left\|f\right\|^2 - 2\sum_{n=0}^N \left\langle f,e_n \right\rangle \left\langle f, e_n \right\rangle + \sum_{n=0}^N \sum_{n'=0}^N \left\langle f,e_n \right\rangle \left\langle f,e_{n'} \right\rangle \left\langle e_n, e_{n'} \right\rangle \\ &= \left\|f\right\|^2 - 2\sum_{n=0}^N \left\langle f,e_n \right\rangle^2 + \sum_{n=0}^N \sum_{n'=0}^N \left\langle f,e_n \right\rangle \left\langle f,e_{n'} \right\rangle \delta_{n,n'} \\ &= \left\|f\right\|^2 - 2\sum_{n=0}^N \left\langle f,e_n \right\rangle^2 + \sum_{n=0}^N \left\langle f,e_n \right\rangle^2 \\ &= \left\|f\right\|^2 - \sum_{n=0}^N \left\langle f,e_n \right\rangle^2 \\ &\to 0 \end{align}
となって完全性が成り立つ。
Diracのデルタ関数
完全正規直交系において、
\begin{align} f(x) &= \lim_{N\to\infty} \sum_{n=0}^N \left\langle f, e_n \right\rangle e_n(x) \\ &= \lim_{N\to\infty} \sum_{n=0}^N \int_\Omega f(y)e_n(y)dy e_n(x) \\ &= \lim_{N\to\infty} \int_\Omega f(y) \left(\sum_{n=0}^N e_n(y)e_n(x)\right) dy \\ \end{align}
という式が成り立つ。
本来\(\sum_{n=0}^\infty e_n(y)e_n(x)\)は\(L^2(\Omega)\)で収束しないが、これを形式的に\(\delta(y,x)\)と表すと、
\begin{align} f(x) &= \int_\Omega f(y) \delta(x,y) dy \\ \end{align}
となる。このような\(\delta(y,x)\)はDiracのデルタ関数と呼ばれる。
逆に\(\sum_{n=0}^\infty e_n(y)e_n(x) = \delta(y,x)\)になるなら
\begin{align} \lim_{N\to\infty} \sum_{n=0}^N \left\langle f, e_n \right\rangle e_n(x) &= \lim_{N\to\infty} \int_\Omega f(y) \left(\sum_{n=0}^N e_n(y)e_n(x)\right) dy \\ &= \int_\Omega f(y) \delta(y,x) dy \\ &= f(x) \end{align}
となり、完全性が成立すると言える。
のデルタ関数の性質としてまず、\(f\)が定数関数\(f(x)=1\)であるとき、
\begin{align} 1 &= \int_\Omega 1 \cdot \delta(y,x) dy \\ &= \int_\Omega \delta(y,x) dy \\ \end{align}
となって、デルタ関数自体の積分は1になる。
また、\(f\)が\(a\)の近傍\(U_a\)の指示関数
\begin{align} f(y)=\chi_{U_a}(y) &= \begin{cases} 1 & \quad (y\in U_a) \\ 0 & \quad (y\notin U_a) \\ \end{cases} \end{align}
である場合を考えると、\(a\neq x\)かつ近傍の大きさが十分小さいとき、つまり\(x\notin U_a\)のとき、
\begin{align} 0 &= \chi_{U_a}(x) \\ &= \int_\Omega \chi_{U_a}(y)\delta(y,x) dy \\ &= \int_{U_a} 1\cdot\delta(y,x) dy \\ &= \int_{U_a} \delta(y,x) dy \\ \end{align}
がどんなに小さい\(U_a\)に対しても成り立つ。これは\(x\notin U_a\)のとき\(\delta(a,x)=0\)であることを意味する。
Fourier基底\(\{\Phi_m(\phi)\}_m\)やLegendre陪多項式\(\{\Theta_{l,m}(\theta)\}_l\)は完全になることが知られている。ここではその証明は省略するが、それぞれ\(\sum_{n=0}^N e_n(y)e_n(x)\)のグラフを見てデルタ関数に近付きそうだということを雰囲気だけ確認しておく。
Φの完全性
\(\{\Phi_m(\phi)\}_m\)に関しては、
\begin{align} &\sum_{m=-M}^M \Phi_m(y)\Phi_m(x) \\ =& \Phi_0(y)\Phi_0(x) + \sum_{m=1}^M \left( \Phi_m(y)\Phi_m(x) + \Phi_{-m}(y)\Phi_{-m}(x) \right) \\ =& \frac{1}{\sqrt{2\pi}}\cdot\frac{1}{\sqrt{2\pi}} + \sum_{m=1}^M \left( \frac{1}{\sqrt{\pi}}\cos(my)\frac{1}{\sqrt{\pi}}\cos(mx) + \frac{1}{\sqrt{\pi}}\sin(my)\frac{1}{\sqrt{\pi}}\sin(mx) \right) \\ =& \frac{1}{\pi}\left( \frac{1}{2} + \sum_{m=1}^M \cos(m(y-x)) \right) \\ =& \frac{1}{\pi\sin\left(\frac{y-x}{2}\right)}\left( \frac{1}{2}\sin\left(\frac{y-x}{2}\right) + \sum_{m=1}^M \cos(m(y-x))\sin\left(\frac{y-x}{2}\right) \right) \\ =& \frac{1}{\pi\sin\left(\frac{y-x}{2}\right)}\left( \frac{1}{2}\sin\left(\frac{y-x}{2}\right) + \frac{1}{2}\sum_{m=1}^M \left( \sin\left((2m+1)\frac{y-x}{2}\right) - \sin\left((2m-1)\frac{y-x}{2}\right) \right) \right) \\ =& \frac{1}{\pi\sin\left(\frac{y-x}{2}\right)}\frac{1}{2} \sin\left((2M+1)\frac{y-x}{2}\right) \\ =& \frac{\sin\left((2M+1)\frac{y-x}{2}\right)}{2\pi\sin\left(\frac{y-x}{2}\right)} \\ \end{align}
となる。
\(\frac{\sin\left((2M+1)z/2\right)}{\sin\left(z/2\right)}\)の部分はDirichlet核として知られる関数である。
\(M\)を増やしてDirichlet核のグラフを見てみる。

\(\frac{\sin\left((2M+1)z/2\right)}{2\pi\sin\left(z/2\right)}\)のグラフ (\(M=1\))
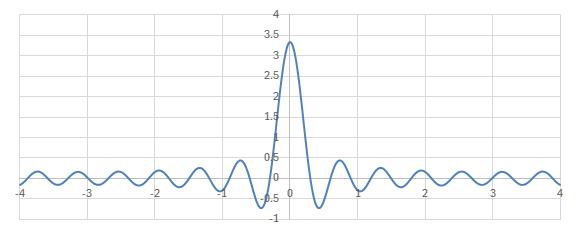
\(\frac{\sin\left((2M+1)z/2\right)}{2\pi\sin\left(z/2\right)}\)のグラフ (\(M=10\))
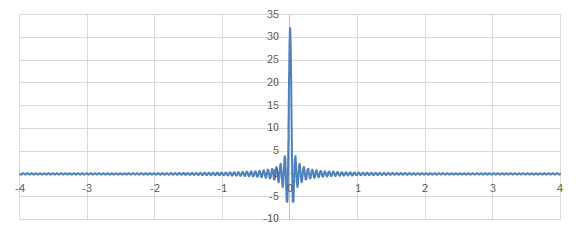
\(\frac{\sin\left((2M+1)z/2\right)}{2\pi\sin\left(z/2\right)}\)のグラフ (\(M=100\))
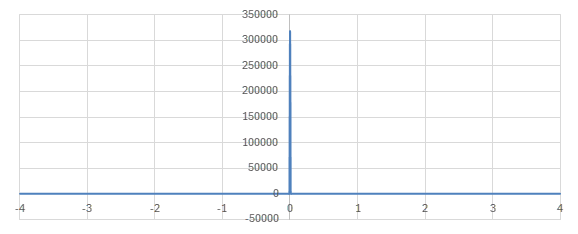
\(\frac{\sin\left((2M+1)z/2\right)}{2\pi\sin\left(z/2\right)}\)のグラフ (\(M=1000000\))
Θの完全性
Legendre陪多項式の場合の核に相当する関数
\begin{align} &\sum_{l=m}^L \sqrt{\frac{(2l+1)(l-m)!}{2(l+m)!}}P_l^m(y)\sqrt{\frac{(2l+1)(l-m)!}{2(l+m)!}}P_l^m(x) \\ =& \frac{(2l+1)(l-m)!}{2(l+m)!} \sum_{l=m}^L P_l^m(y)P_l^m(x) \end{align}
のグラフを見てみる。
横軸が\(y\)。青いグラフは\(x=0\)の場合で、赤いグラフは\(x=0.7\)の場合。
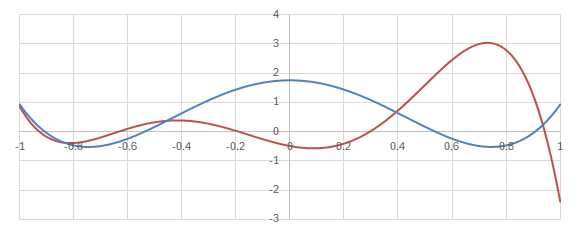
Legendre陪多項式による核のグラフ (\(m=0, L=5\))

Legendre陪多項式による核のグラフ (\(m=0, L=20\))

Legendre陪多項式による核のグラフ (\(m=0, L=100\))
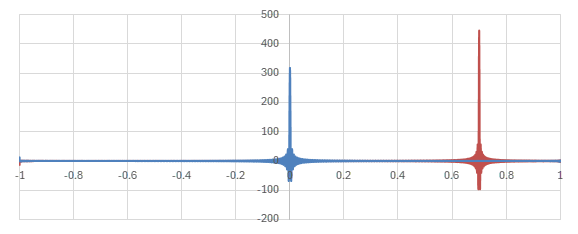
Legendre陪多項式による核のグラフ (\(m=0, L=1000\))
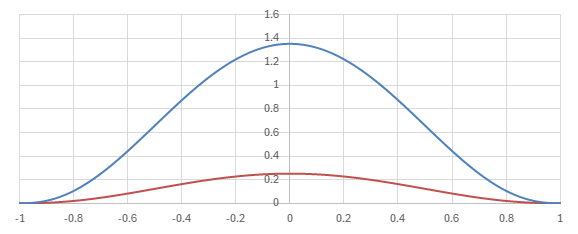
Legendre陪多項式による核のグラフ (\(m=5, L=5\))
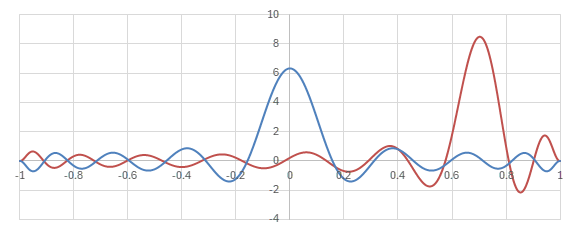
Legendre陪多項式による核のグラフ (\(m=5, L=20\))
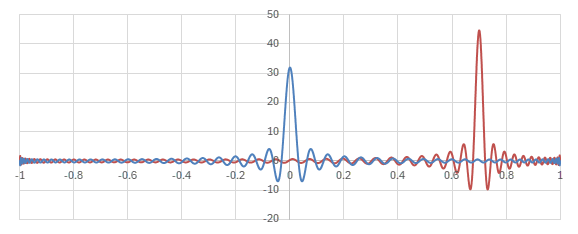
Legendre陪多項式による核のグラフ (\(m=5, L=100\))
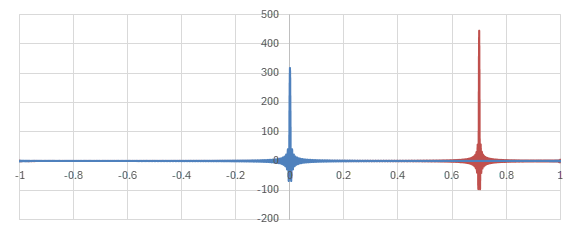
Legendre陪多項式による核のグラフ (\(m=5, L=1000\))
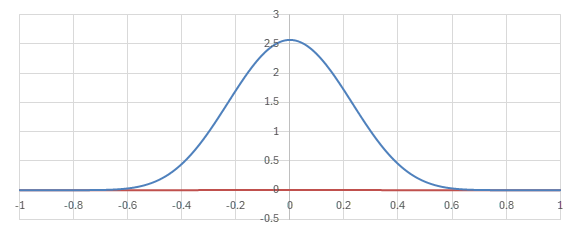
Legendre陪多項式による核のグラフ (\(m=20, L=20\))
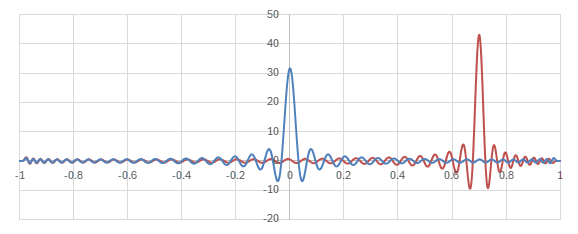
Legendre陪多項式による核のグラフ (\(m=20, L=100\))
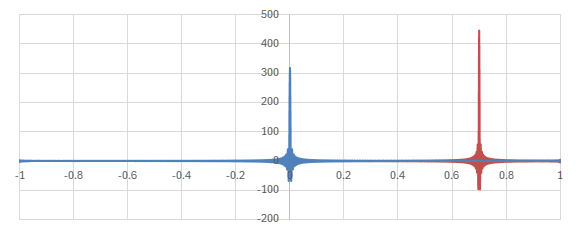
Legendre陪多項式による核のグラフ (\(m=20, L=1000\))
Yの完全性
\(\{\Phi_m(\phi)\}_m\)と\(\{\Theta_{l,m}(\theta)\}_l\)の完全性を認めるとして、\(\{Y_{l,m}(\theta,\phi)\}_{l,m}\)に関しても大雑把に言えば
\begin{align} f(\theta,\phi) &= \sum_{m=-\infty}^\infty \left( \int_0^{2\pi} f(\theta,\phi')\Phi_m(\phi)d\phi' \right) \Phi_m(\phi) \\ &= \sum_{m=-\infty}^\infty \left( \int_0^{2\pi} \sum_{l=|m|}^\infty \left( \int_0^\pi f(\theta',\phi')\Theta_{l,m}(\theta')\sin(\theta')d\theta'\right) \Theta_{l,m}(\theta) \Phi_m(\phi')d\phi' \right) \Phi_m(\phi) \\ &= \sum_{m=-\infty}^\infty \sum_{l=|m|}^\infty \left( \int_0^{2\pi} \int_0^\pi f(\theta',\phi')\Theta_{l,m}(\theta') \Phi_m(\phi')\sin(\theta')d\theta'd\phi' \right) \Theta_{l,m}(\theta) \Phi_m(\phi) \\ &= \sum_{l=0}^\infty \sum_{m=-l}^l \left( \int_{S^2} f(\theta',\phi')Y_{l,m}(\theta',\phi')d\Omega \right) Y_{l,m}(\theta,\phi) \\ \end{align}
という完全性が成り立つ。(厳密には総和と積分の交換や、\(Y_{l,m}(\theta,\cdot)\in L^2([0,2\pi])\)となるかどうかなどの問題がある)
係数は\(Y_{l,m}(\theta,\phi)\Theta_{l,m}(\theta)\Phi_m(\phi)\)の球面全体での積分によって求めることができる。
球面調和関数の直交座標表示
\((x,y,z)\)が球面上にあるとき、
\begin{align} \left\{ \begin{array}{ll} x &= \sin(\theta)\cos(\phi) \\ y &= \sin(\theta)\sin(\phi) \\ z &= \cos(\theta) \\ \end{array} \right. \end{align}
となる。
このとき、
\begin{align} P_l^m(\cos(\theta)) &= (1-\cos(\theta)^2)^{m/2}P_l^{(m)}(\cos(\theta)) \\ &= \sin(\theta)^mP_l^{(m)}(z) \end{align}
と、一部を\(z\)で表すことができる。
ここで、\(P_l^{(m)}\)はLegendre多項式\(P_l\)の\(m\)階導関数。
また、
\begin{align} &\cos(m\phi) + i\sin(m\phi) \\ =& e^{im\phi} \\ =& \left(e^{i\phi}\right)^m \\ =& \left(\cos(\phi)+i\sin(\phi)\right)^m \\ =& \sum_{k=0}^m \binom{m}{k}\cos(\phi)^{m-k}(i\sin(\phi))^k \\ =& \sum_{0\leq 2k\leq m} \binom{m}{2k}\cos(\phi)^{m-2k}(i\sin(\phi))^{2k} + \sum_{1\leq 2k+1\leq m} \binom{m}{2k+1}\cos(\phi)^{m-2k-1}(i\sin(\phi))^{2k+1} \\ =& \sum_{0\leq 2k\leq m} (-1)^k\binom{m}{2k}\cos(\phi)^{m-2k}\sin(\phi)^{2k} + i\sum_{1\leq 2k+1\leq m} (-1)^k\binom{m}{2k+1}\cos(\phi)^{m-2k-1}\sin(\phi)^{2k+1} \\ \end{align}
なので、\(P_l^m(\cos(\theta))\)で処理できなかった\(\sin(\theta)^m\)をこちら側に押し付けると、
\begin{align} &\sin(\theta)^m\left(\cos(m\phi) + i\sin(m\phi)\right) \\ =& \sin(\theta)^m\left(\sum_{0\leq 2k\leq m} (-1)^k\binom{m}{2k}\cos(\phi)^{m-2k}\sin(\phi)^{2k} + i\sum_{1\leq 2k+1\leq m} (-1)^k\binom{m}{2k+1}\cos(\phi)^{m-2k-1}\sin(\phi)^{2k+1}\right) \\ =& \sum_{0\leq 2k\leq m} (-1)^k\binom{m}{2k}x^{m-2k}y^{2k} + i\sum_{1\leq 2k+1\leq m} (-1)^k\binom{m}{2k+1}x^{m-2k-1}y^{2k+1} \\ \end{align}
となる。
したがって、\(m>0\)のとき、
\begin{align} Y_{l,m}(\theta,\phi) &= \sqrt{\frac{(2l+1)(l-m)!}{2\pi(l+m)!}}P_l^m(\cos(\theta))\cos(m\phi) \\ &= \sqrt{\frac{(2l+1)(l-m)!}{2\pi(l+m)!}}P_l^{(m)}(z)\sum_{0\leq 2k\leq m} (-1)^k\binom{m}{2k}x^{m-2k}y^{2k} \\ \end{align}
\(m=0\)のとき、
\begin{align} Y_{l,m}(\theta,\phi) &= \sqrt{\frac{2l+1}{4\pi}}P_l(\cos(\theta)) \\ &= \sqrt{\frac{2l+1}{4\pi}}P_l(z) \\ \end{align}
\(m<0\)のとき、
\begin{align} Y_{l,m}(\theta,\phi) &= \sqrt{\frac{(2l+1)(l-|m|)!}{2\pi(l+|m|)!}}P_l^{|m|}(\cos(\theta))\sin(|m|\phi) \\ &= \sqrt{\frac{(2l+1)(l-|m|)!}{2\pi(l+|m|)!}}P_l^{(|m|)}(z)\sum_{1\leq 2k+1\leq |m|} (-1)^k\binom{|m|}{2k+1}x^{|m|-2k-1}y^{2k+1} \end{align}
となり、\(Y_{l,m}(\theta,\phi)\)を\(x,y,z\)の多項式で表すことができる。
まとめ
これまで考察した結果を以下にまとめる。
3次元Laplace方程式
\begin{align} 0 &= \Delta\psi(x,y,z) \\ &= \partial_x^2\psi(x,y,z) + \partial_y^2\psi(x,y,z) + \partial_z^2\psi(x,y,z) \end{align}
に、極座標の変数分離法
\begin{align} \psi(x,y,z) = R(r)\Theta(\theta)\Phi(\phi) \end{align}
を適用すると、それぞれの因子は次の方程式を満たさなければならない。
\begin{align} 0 &= \partial_r(r^2\partial_rR(r)) - l(l+1) R(r) \\ 0 &= \partial_\phi^2\Phi(\phi) + m^2\Phi(\phi) \\ 0 &= \frac{d}{dw}\left((1-w^2)\frac{d}{dw}\Theta(\theta)\right) + \left( l(l+1) - \frac{m^2}{(1-w^2)} \right)\Theta(\theta) \\ \end{align}
ここで\(w=\cos(\theta)\)であり、\(\Theta\)が満たすべき上記の方程式をLegendre陪方程式と言う。
これらの(正則な)解は、次のように表される。(\(c_1, c_2, c_3, c_4, c_5\)は定数)
\begin{align} R(r) &= c_1r^l + c_2r^{-1-l} \\ \Theta(\theta) &= c_3P_l^m(\cos(\theta)) \\ \Phi(\phi) &= c_4\sin(m\phi) + c_5\cos(m\phi) \end{align}
ここで、\(P_l^m\)はLegendre陪多項式。
上記のLalpalce方程式の解について、
\begin{align} \Phi_m(\phi) := \begin{cases} \frac{1}{\sqrt{\pi}}\cos(m\phi) &\qquad (m>0) \\ \frac{1}{\sqrt{2\pi}} &\qquad (m=0) \\ \frac{1}{\sqrt{\pi}}\sin(-m\phi) &\qquad (m<0) \\ \end{cases} \end{align}
とすると、\(\Phi_m\)は\(L^2([0,2\pi])\)における完全正規直交系になる。
また、
\begin{align} \Theta_{l,m}(\theta) &= \sqrt{\frac{(2l+1)(l-m)!}{2(l+m)!}}P_l^m(\cos(\theta)) \\ \end{align}
とすると、\(\Theta_{l,m}\)は\(L^2([0,\pi])\)における完全正規直交系になる。
これらを用いると、Laplace方程式の解の角度依存成分は
\begin{align} Y_{l,m}(\theta,\phi) &= \Theta_{l,m}(\theta)\Phi_m(\phi) = \begin{cases} \sqrt{\frac{(2l+1)(l-m)!}{2\pi(l+m)!}}P_l^m(\cos(\theta))\cos(m\phi) &\qquad (m>0) \\ \sqrt{\frac{2l+1}{4\pi}}P_l(\cos(\theta)) &\qquad (m=0) \\ \sqrt{\frac{(2l+1)(l-|m|)!}{2\pi(l+|m|)!}}P_l^{|m|}(\cos(\theta))\sin(|m|\phi) &\qquad (m<0) \\ \end{cases} \end{align}
と表すことができ、この関数を球面調和関数と言う。
\(\Theta_{l,m}(\theta), \Phi_m(\phi)\)がそれぞれ完全正規直交系であることから、\(Y_{l,m}(\theta,\phi)\)も球面上で完全正規直交系になる。
これはつまり、任意の\(f(\theta,\phi)\in L^2(S^2)\)に対して、
\begin{align} c_{l,m} &= \int_{S^2} f(\theta,\phi)Y_{l,m}(\theta,\phi)d\Omega \\ &= \int_0^{2\pi} \int_0^\pi f(\theta,\phi)Y_{l,m}(\theta,\phi)\sin(\theta)d\theta d\phi \\ \end{align}
とすると、
\begin{align} f(\theta,\phi) &= \sum_{l=0}^\infty \sum_{m=-l}^l c_{l,m}Y_{l,m}(\theta,\phi) \\ \end{align}
が成り立つということである。
\(x,y,z\)を
\begin{align} \left\{ \begin{array}{ll} x &= \sin(\theta)\cos(\phi) \\ y &= \sin(\theta)\sin(\phi) \\ z &= \cos(\theta) \\ \end{array} \right. \end{align}
と定義すると、球面調和関数は次のように多項式で表すことができる。
- \(m>0\)のとき、
\begin{align} Y_{l,m}(\theta,\phi) &= \sqrt{\frac{(2l+1)(l-m)!}{2\pi(l+m)!}}P_l^{(m)}(z)\sum_{0\leq 2k\leq m} (-1)^k\binom{m}{2k}x^{m-2k}y^{2k} \\ \end{align}
- \(m=0\)のとき、
\begin{align} Y_{l,m}(\theta,\phi) &= \sqrt{\frac{2l+1}{4\pi}}P_l(z) \\ \end{align}
- \(m<0\)のとき、
\begin{align} Y_{l,m}(\theta,\phi) &= \sqrt{\frac{(2l+1)(l-|m|)!}{2\pi(l+|m|)!}}P_l^{(|m|)}(z)\sum_{1\leq 2k+1\leq |m|} (-1)^k\binom{|m|}{2k+1}x^{|m|-2k-1}y^{2k+1} \end{align}
実球面調和関数の一覧
\(l=10\)までの実球面調和関数を次の表に列挙する。
| \(m\) | \(\Phi_m(\phi)\) | \(l\) | \(P_l^{|m|}(w)\) | \(Y_{l,m}(\theta,\phi)\) | \(Y_{l,m}(\theta,\phi)\) (直交座標表示) |
|---|---|---|---|---|---|
| -10 | \(\frac{1}{\sqrt{\pi}}\sin(10\phi)\) | 10 | \(654729075(1-w^2)^5\) | \(\frac{\sqrt{21}}{7257600\sqrt{92378\pi}}\sin(10\phi)\) | \(\frac{\sqrt{969969}}{512\sqrt{2\pi}}(10x^9y-120x^7y^3+252x^5y^5-120x^3y^7+10xy^9)\) |
| -9 | \(\frac{1}{\sqrt{\pi}}\sin(9\phi)\) | 9 | \(34459425(1-w^2)^{9/2}\) | \(\frac{\sqrt{19}}{725760\sqrt{24310\pi}}\sin(9\phi)\) | \(\frac{\sqrt{230945}}{256\sqrt{2\pi}}(9x^8y-84x^6y^3+126x^4y^5-36x^2y^7+y^9)\) |
| 10 | \(654729075w(1-w^2)^{9/2}\) | \(\frac{\sqrt{21}}{725760\sqrt{461890\pi}}\cos(\theta)\sin(9\phi)\) | \(\frac{\sqrt{4849845}}{256\sqrt{2\pi}}(9x^8y-84x^6y^3+126x^4y^5-36x^2y^7+y^9)z\) | ||
| -8 | \(\frac{1}{\sqrt{\pi}}\sin(8\phi)\) | 8 | \(2027025(1-w^2)^4\) | \(\frac{\sqrt{17}}{241920\sqrt{715\pi}}\sin(8\phi)\) | \(\frac{3\sqrt{12155}}{256\sqrt{\pi}}(8x^7y-56x^5y^3+56x^3y^5-8xy^7)\) |
| 9 | \(34459425w(1-w^2)^4\) | \(\frac{\sqrt{19}}{241920\sqrt{12155\pi}}\cos(\theta)\sin(8\phi)\) | \(\frac{3\sqrt{230945}}{256\sqrt{\pi}}(8x^7y-56x^5y^3+56x^3y^5-8xy^7)z\) | ||
| 10 | \(\frac{34459425}{2}(19w^2-1)(1-w^2)^4\) | \(\frac{\sqrt{21}}{725760\sqrt{12155\pi}}(19\cos(\theta)^2-1)\sin(8\phi)\) | \(\frac{\sqrt{255255}}{512\sqrt{\pi}}(8x^7y-56x^5y^3+56x^3y^5-8xy^7)(19z^2-1)\) | ||
| -7 | \(\frac{1}{\sqrt{\pi}}\sin(7\phi)\) | 7 | \(135135(1-w^2)^{7/2}\) | \(\frac{\sqrt{15}}{20160\sqrt{143\pi}}\sin(7\phi)\) | \(\frac{3\sqrt{2145}}{64\sqrt{\pi}}(7x^6y-35x^4y^3+21x^2y^5-y^7)\) |
| 8 | \(2027025w(1-w^2)^{7/2}\) | \(\frac{\sqrt{17}}{60480\sqrt{715\pi}}\cos(\theta)\sin(7\phi)\) | \(\frac{3\sqrt{12155}}{64\sqrt{\pi}}(7x^6y-35x^4y^3+21x^2y^5-y^7)z\) | ||
| 9 | \(\frac{2027025}{2}(17w^2-1)(1-w^2)^{7/2}\) | \(\frac{\sqrt{19}}{120960\sqrt{1430\pi}}(17\cos(\theta)^2-1)\sin(7\phi)\) | \(\frac{3\sqrt{13585}}{256\sqrt{2\pi}}(7x^6y-35x^4y^3+21x^2y^5-y^7)(17z^2-1)\) | ||
| 10 | \(\frac{11486475}{2}(19w^3-3w)(1-w^2)^{7/2}\) | \(\frac{\sqrt{21}}{40320\sqrt{24310\pi}}(19\cos(\theta)^3-3\cos(\theta))\sin(7\phi)\) | \(\frac{3\sqrt{255255}}{256\sqrt{2\pi}}(7x^6y-35x^4y^3+21x^2y^5-y^7)(19z^3-3z)\) | ||
| -6 | \(\frac{1}{\sqrt{\pi}}\sin(6\phi)\) | 6 | \(10395(1-w^2)^3\) | \(\frac{\sqrt{13}}{1440\sqrt{462\pi}}\sin(6\phi)\) | \(\frac{\sqrt{3003}}{32\sqrt{2\pi}}(6x^5y-20x^3y^3+6xy^5)\) |
| 7 | \(135135w(1-w^2)^3\) | \(\frac{\sqrt{15}}{1440\sqrt{2002\pi}}\cos(\theta)\sin(6\phi)\) | \(\frac{3\sqrt{15015}}{32\sqrt{2\pi}}(6x^5y-20x^3y^3+6xy^5)z\) | ||
| 8 | \(\frac{135135}{2}(15w^2-1)(1-w^2)^3\) | \(\frac{\sqrt{17}}{10080\sqrt{858\pi}}(15\cos(\theta)^2-1)\sin(6\phi)\) | \(\frac{\sqrt{7293}}{64\sqrt{2\pi}}(6x^5y-20x^3y^3+6xy^5)(15z^2-1)\) | ||
| 9 | \(\frac{675675}{2}(17w^3-3w)(1-w^2)^3\) | \(\frac{\sqrt{19}}{10080\sqrt{4290\pi}}(17\cos(\theta)^3-3\cos(\theta))\sin(6\phi)\) | \(\frac{\sqrt{40755}}{64\sqrt{2\pi}}(6x^5y-20x^3y^3+6xy^5)(17z^3-3z)\) | ||
| 10 | \(\frac{675675}{8}(323w^4-102w^2+3)(1-w^2)^3\) | \(\frac{\sqrt{21}}{20160\sqrt{1430\pi}}(323\cos(\theta)^4-102\cos(\theta)^2+3)\sin(6\phi)\) | \(\frac{3\sqrt{15015}}{512\sqrt{2\pi}}(6x^5y-20x^3y^3+6xy^5)(323z^4-102z^2+3)\) | ||
| -5 | \(\frac{1}{\sqrt{\pi}}\sin(5\phi)\) | 5 | \(945(1-w^2)^{5/2}\) | \(\frac{\sqrt{11}}{720\sqrt{14\pi}}\sin(5\phi)\) | \(\frac{3\sqrt{77}}{16\sqrt{2\pi}}(5x^4y-10x^2y^3+y^5)\) |
| 6 | \(10395w(1-w^2)^{5/2}\) | \(\frac{\sqrt{13}}{720\sqrt{154\pi}}\cos(\theta)\sin(5\phi)\) | \(\frac{3\sqrt{1001}}{16\sqrt{2\pi}}(5x^4y-10x^2y^3+y^5)z\) | ||
| 7 | \(\frac{10395}{2}(13w^2-1)(1-w^2)^{5/2}\) | \(\frac{\sqrt{15}}{1440\sqrt{77\pi}}(13\cos(\theta)^2-1)\sin(5\phi)\) | \(\frac{3\sqrt{1155}}{64\sqrt{\pi}}(5x^4y-10x^2y^3+y^5)(13z^2-1)\) | ||
| 8 | \(\frac{135135}{2}(5w^3-w)(1-w^2)^{5/2}\) | \(\frac{\sqrt{17}}{1440\sqrt{1001\pi}}(5\cos(\theta)^3-\cos(\theta))\sin(5\phi)\) | \(\frac{3\sqrt{17017}}{64\sqrt{\pi}}(5x^4y-10x^2y^3+y^5)(5z^3-z)\) | ||
| 9 | \(\frac{135135}{8}(85w^4-30w^2+1)(1-w^2)^{5/2}\) | \(\frac{\sqrt{19}}{5040\sqrt{286\pi}}(85\cos(\theta)^4-30\cos(\theta)^2+1)\sin(5\phi)\) | \(\frac{3\sqrt{2717}}{128\sqrt{2\pi}}(5x^4y-10x^2y^3+y^5)(85z^4-30z^2+1)\) | ||
| 10 | \(\frac{135135}{8}(323w^5-170w^3+15w)(1-w^2)^{5/2}\) | \(\frac{\sqrt{21}}{5040\sqrt{286\pi}}(323\cos(\theta)^5-170\cos(\theta)^3+15\cos(\theta))\sin(5\phi)\) | \(\frac{3\sqrt{3003}}{128\sqrt{2\pi}}(5x^4y-10x^2y^3+y^5)(323z^5-170z^3+15z)\) | ||
| -4 | \(\frac{1}{\sqrt{\pi}}\sin(4\phi)\) | 4 | \(105(1-w^2)^2\) | \(\frac{\sqrt{9}}{48\sqrt{35\pi}}\sin(4\phi)\) | \(\frac{3\sqrt{35}}{16\sqrt{\pi}}(4x^3y-4xy^3)\) |
| 5 | \(945w(1-w^2)^2\) | \(\frac{\sqrt{11}}{144\sqrt{35\pi}}\cos(\theta)\sin(4\phi)\) | \(\frac{3\sqrt{385}}{16\sqrt{\pi}}(4x^3y-4xy^3)z\) | ||
| 6 | \(\frac{945}{2}(11w^2-1)(1-w^2)^2\) | \(\frac{\sqrt{13}}{720\sqrt{7\pi}}(11\cos(\theta)^2-1)\sin(4\phi)\) | \(\frac{3\sqrt{91}}{32\sqrt{\pi}}(4x^3y-4xy^3)(11z^2-1)\) | ||
| 7 | \(\frac{3465}{2}(13w^3-3w)(1-w^2)^2\) | \(\frac{\sqrt{15}}{240\sqrt{77\pi}}(13\cos(\theta)^3-3\cos(\theta))\sin(4\phi)\) | \(\frac{3\sqrt{1155}}{32\sqrt{\pi}}(4x^3y-4xy^3)(13z^3-3z)\) | ||
| 8 | \(\frac{10395}{8}(65w^4-26w^2+1)(1-w^2)^2\) | \(\frac{\sqrt{17}}{720\sqrt{77\pi}}(65\cos(\theta)^4-26\cos(\theta)^2+1)\sin(4\phi)\) | \(\frac{3\sqrt{1309}}{128\sqrt{\pi}}(4x^3y-4xy^3)(65z^4-26z^2+1)\) | ||
| 9 | \(\frac{135135}{8}(17w^5-10w^3+w)(1-w^2)^2\) | \(\frac{\sqrt{19}}{144\sqrt{5005\pi}}(17\cos(\theta)^5-10\cos(\theta)^3+\cos(\theta))\sin(4\phi)\) | \(\frac{3\sqrt{95095}}{128\sqrt{\pi}}(4x^3y-4xy^3)(17z^5-10z^3+z)\) | ||
| 10 | \(\frac{45045}{16}(323w^6-255w^4+45w^2-1)(1-w^2)^2\) | \(\frac{\sqrt{21}}{336\sqrt{715\pi}}(323\cos(\theta)^6-255\cos(\theta)^4+45\cos(\theta)^2-1)\sin(4\phi)\) | \(\frac{3\sqrt{15015}}{256\sqrt{\pi}}(4x^3y-4xy^3)(323z^6-255z^4+45z^2-1)\) | ||
| -3 | \(\frac{1}{\sqrt{\pi}}\sin(3\phi)\) | 3 | \(15(1-w^2)^{3/2}\) | \(\frac{\sqrt{7}}{12\sqrt{10\pi}}\sin(3\phi)\) | \(\frac{\sqrt{35}}{4\sqrt{2\pi}}(3x^2y-y^3)\) |
| 4 | \(105w(1-w^2)^{3/2}\) | \(\frac{\sqrt{9}}{12\sqrt{70\pi}}\cos(\theta)\sin(3\phi)\) | \(\frac{3\sqrt{35}}{4\sqrt{2\pi}}(3x^2y-y^3)z\) | ||
| 5 | \(\frac{105}{2}(9w^2-1)(1-w^2)^{3/2}\) | \(\frac{\sqrt{11}}{24\sqrt{70\pi}}(9\cos(\theta)^2-1)\sin(3\phi)\) | \(\frac{\sqrt{385}}{16\sqrt{2\pi}}(3x^2y-y^3)(9z^2-1)\) | ||
| 6 | \(\frac{315}{2}(11w^3-3w)(1-w^2)^{3/2}\) | \(\frac{\sqrt{13}}{24\sqrt{210\pi}}(11\cos(\theta)^3-3\cos(\theta))\sin(3\phi)\) | \(\frac{\sqrt{1365}}{16\sqrt{2\pi}}(3x^2y-y^3)(11z^3-3z)\) | ||
| 7 | \(\frac{315}{8}(143w^4-66w^2+3)(1-w^2)^{3/2}\) | \(\frac{\sqrt{15}}{120\sqrt{7\pi}}(143\cos(\theta)^4-66\cos(\theta)^2+3)\sin(3\phi)\) | \(\frac{3\sqrt{105}}{64\sqrt{\pi}}(3x^2y-y^3)(143z^4-66z^2+3)\) | ||
| 8 | \(\frac{3465}{8}(39w^5-26w^3+3w)(1-w^2)^{3/2}\) | \(\frac{\sqrt{17}}{24\sqrt{1155\pi}}(39\cos(\theta)^5-26\cos(\theta)^3+3\cos(\theta))\sin(3\phi)\) | \(\frac{\sqrt{19635}}{64\sqrt{\pi}}(3x^2y-y^3)(39z^5-26z^3+3z)\) | ||
| 9 | \(\frac{3465}{16}(221w^6-195w^4+39w^2-1)(1-w^2)^{3/2}\) | \(\frac{\sqrt{19}}{24\sqrt{2310\pi}}(221\cos(\theta)^6-195\cos(\theta)^4+39\cos(\theta)^2-1)\sin(3\phi)\) | \(\frac{\sqrt{21945}}{128\sqrt{2\pi}}(3x^2y-y^3)(221z^6-195z^4+39z^2-1)\) | ||
| 10 | \(\frac{6435}{16}(323w^7-357w^5+105w^3-7w)(1-w^2)^{3/2}\) | \(\frac{\sqrt{21}}{24\sqrt{1430\pi}}(323\cos(\theta)^7-357\cos(\theta)^5+105\cos(\theta)^3-7\cos(\theta))\sin(3\phi)\) | \(\frac{3\sqrt{15015}}{128\sqrt{2\pi}}(3x^2y-y^3)(323z^7-357z^5+105z^3-7z)\) | ||
| -2 | \(\frac{1}{\sqrt{\pi}}\sin(2\phi)\) | 2 | \(3(1-w^2)\) | \(\frac{\sqrt{5}}{4\sqrt{3\pi}}\sin(2\phi)\) | \(\frac{\sqrt{15}}{4\sqrt{\pi}}2xy\) |
| 3 | \(15w(1-w^2)\) | \(\frac{\sqrt{7}}{4\sqrt{15\pi}}\cos(\theta)\sin(2\phi)\) | \(\frac{\sqrt{105}}{4\sqrt{\pi}}2xyz\) | ||
| 4 | \(\frac{15}{2}(7w^2-1)(1-w^2)\) | \(\frac{\sqrt{9}}{12\sqrt{5\pi}}(7\cos(\theta)^2-1)\sin(2\phi)\) | \(\frac{3\sqrt{5}}{8\sqrt{\pi}}2xy(7z^2-1)\) | ||
| 5 | \(\frac{105}{2}(3w^3-w)(1-w^2)\) | \(\frac{\sqrt{11}}{4\sqrt{105\pi}}(3\cos(\theta)^3-\cos(\theta))\sin(2\phi)\) | \(\frac{\sqrt{1155}}{8\sqrt{\pi}}2xy(3z^3-z)\) | ||
| 6 | \(\frac{105}{8}(33w^4-18w^2+1)(1-w^2)\) | \(\frac{\sqrt{13}}{4\sqrt{210\pi}}(33\cos(\theta)^4-18\cos(\theta)^2+1)\sin(2\phi)\) | \(\frac{\sqrt{1365}}{32\sqrt{2\pi}}2xy(33z^4-18z^2+1)\) | ||
| 7 | \(\frac{63}{8}(143w^5-110w^3+15w)(1-w^2)\) | \(\frac{\sqrt{15}}{12\sqrt{14\pi}}(143\cos(\theta)^5-110\cos(\theta)^3+15\cos(\theta))\sin(2\phi)\) | \(\frac{3\sqrt{105}}{32\sqrt{2\pi}}2xy(143z^5-110z^3+15z)\) | ||
| 8 | \(\frac{315}{16}(143w^6-143w^4+33w^2-1)(1-w^2)\) | \(\frac{\sqrt{17}}{12\sqrt{70\pi}}(143\cos(\theta)^6-143\cos(\theta)^4+33\cos(\theta)^2-1)\sin(2\phi)\) | \(\frac{3\sqrt{595}}{64\sqrt{2\pi}}2xy(143z^6-143z^4+33z^2-1)\) | ||
| 9 | \(\frac{495}{16}(221w^7-273w^5+91w^3-7w)(1-w^2)\) | \(\frac{\sqrt{19}}{12\sqrt{110\pi}}(221\cos(\theta)^7-273\cos(\theta)^5+91\cos(\theta)^3-7\cos(\theta))\sin(2\phi)\) | \(\frac{3\sqrt{1045}}{64\sqrt{2\pi}}2xy(221z^7-273z^5+91z^3-7z)\) | ||
| 10 | \(\frac{495}{128}(4199w^8-6188w^6+2730w^4-364w^2+7)(1-w^2)\) | \(\frac{\sqrt{21}}{12\sqrt{55\pi}}(4199\cos(\theta)^8-6188\cos(\theta)^6+2730\cos(\theta)^4-364\cos(\theta)^2+7)\sin(2\phi)\) | \(\frac{3\sqrt{1155}}{512\sqrt{\pi}}2xy(4199z^8-6188z^6+2730z^4-364z^2+7)\) | ||
| -1 | \(\frac{1}{\sqrt{\pi}}\sin(\phi)\) | 1 | \((1-w^2)^{1/2}\) | \(\frac{\sqrt{3}}{2\sqrt{\pi}}\sin(\phi)\) | \(\frac{\sqrt{3}}{2\sqrt{\pi}}y\) |
| 2 | \(3w(1-w^2)^{1/2}\) | \(\frac{\sqrt{5}}{2\sqrt{3\pi}}\cos(\theta)\sin(\phi)\) | \(\frac{\sqrt{15}}{2\sqrt{\pi}}yz\) | ||
| 3 | \(\frac{3}{2}(5w^2-1)(1-w^2)^{1/2}\) | \(\frac{\sqrt{7}}{2\sqrt{6\pi}}(5\cos(\theta)^2-1)\sin(\phi)\) | \(\frac{\sqrt{21}}{4\sqrt{2\pi}}y(5z^2-1)\) | ||
| 4 | \(\frac{5}{2}(7w^3-3w)(1-w^2)^{1/2}\) | \(\frac{\sqrt{9}}{2\sqrt{10\pi}}(7\cos(\theta)^3-3\cos(\theta))\sin(\phi)\) | \(\frac{3\sqrt{5}}{4\sqrt{2\pi}}y(7z^3-3z)\) | ||
| 5 | \(\frac{15}{8}(21w^4-14w^2+1)(1-w^2)^{1/2}\) | \(\frac{\sqrt{11}}{2\sqrt{15\pi}}(21\cos(\theta)^4-14\cos(\theta)^2+1)\sin(\phi)\) | \(\frac{\sqrt{165}}{16\sqrt{\pi}}y(21z^4-14z^2+1)\) | ||
| 6 | \(\frac{21}{8}(33w^5-30w^3+5w)(1-w^2)^{1/2}\) | \(\frac{\sqrt{13}}{2\sqrt{21\pi}}(33\cos(\theta)^5-30\cos(\theta)^3+5\cos(\theta))\sin(\phi)\) | \(\frac{\sqrt{273}}{16\sqrt{\pi}}y(33z^5-30z^3+5z)\) | ||
| 7 | \(\frac{7}{16}(429w^6-495w^4+135w^2-5)(1-w^2)^{1/2}\) | \(\frac{\sqrt{15}}{4\sqrt{7\pi}}(429\cos(\theta)^6-495\cos(\theta)^4+135\cos(\theta)^2-5)\sin(\phi)\) | \(\frac{\sqrt{105}}{64\sqrt{\pi}}y(429z^6-495z^4+135z^2-5)\) | ||
| 8 | \(\frac{9}{16}(715w^7-1001w^5+385w^3-35w)(1-w^2)^{1/2}\) | \(\frac{\sqrt{17}}{12\sqrt{\pi}}(715\cos(\theta)^7-1001\cos(\theta)^5+385\cos(\theta)^3-35\cos(\theta))\sin(\phi)\) | \(\frac{3\sqrt{17}}{64\sqrt{\pi}}y(715z^7-1001z^5+385z^3-35z)\) | ||
| 9 | \(\frac{45}{128}(2431w^8-4004w^6+2002w^4-308w^2+7)(1-w^2)^{1/2}\) | \(\frac{\sqrt{19}}{6\sqrt{5\pi}}(2431\cos(\theta)^8-4004\cos(\theta)^6+2002\cos(\theta)^4-308\cos(\theta)^2+7)\sin(\phi)\) | \(\frac{3\sqrt{95}}{256\sqrt{\pi}}y(2431z^8-4004z^6+2002z^4-308z^2+7)\) | ||
| 10 | \(\frac{55}{128}(4199w^9-7956w^7+4914w^5-1092w^3+63w)(1-w^2)^{1/2}\) | \(\frac{\sqrt{21}}{2\sqrt{55\pi}}(4199\cos(\theta)^9-7956\cos(\theta)^7+4914\cos(\theta)^5-1092\cos(\theta)^3+63\cos(\theta))\sin(\phi)\) | \(\frac{\sqrt{1155}}{256\sqrt{\pi}}y(4199z^9-7956z^7+4914z^5-1092z^3+63z)\) | ||
| 0 | \(\frac{1}{\sqrt{2\pi}}\) | 0 | \(1\) | \(\frac{1}{2\sqrt{\pi}}\) | \(\frac{1}{2\sqrt{\pi}}\) |
| 1 | \(w\) | \(\frac{\sqrt{3}}{2\sqrt{\pi}}\cos(\theta)\) | \(\frac{\sqrt{3}}{2\sqrt{\pi}}z\) | ||
| 2 | \(\frac{1}{2}(3w^2-1)\) | \(\frac{\sqrt{5}}{2\sqrt{\pi}}(3\cos(\theta)^2-1)\) | \(\frac{\sqrt{5}}{4\sqrt{\pi}}(3z^2-1)\) | ||
| 3 | \(\frac{1}{2}(5w^3-3w)\) | \(\frac{\sqrt{7}}{2\sqrt{\pi}}(5\cos(\theta)^3-3\cos(\theta))\) | \(\frac{\sqrt{7}}{4\sqrt{\pi}}(5z^3-3z)\) | ||
| 4 | \(\frac{1}{8}(35w^4-30w^2+3)\) | \(\frac{\sqrt{9}}{2\sqrt{\pi}}(35\cos(\theta)^4-30\cos(\theta)^2+3)\) | \(\frac{3}{16\sqrt{\pi}}(35z^4-30z^2+3)\) | ||
| 5 | \(\frac{1}{8}(63w^5-70w^3+15w)\) | \(\frac{\sqrt{11}}{2\sqrt{\pi}}(63\cos(\theta)^5-70\cos(\theta)^3+15\cos(\theta))\) | \(\frac{\sqrt{11}}{16\sqrt{\pi}}(63z^5-70z^3+15z)\) | ||
| 6 | \(\frac{1}{16}(231w^6-315w^4+105w^2-5)\) | \(\frac{\sqrt{13}}{2\sqrt{\pi}}(231\cos(\theta)^6-315\cos(\theta)^4+105\cos(\theta)^2-5)\) | \(\frac{\sqrt{13}}{32\sqrt{\pi}}(231z^6-315z^4+105z^2-5)\) | ||
| 7 | \(\frac{1}{16}(429w^7-693w^5+315w^3-35w)\) | \(\frac{\sqrt{15}}{2\sqrt{\pi}}(429\cos(\theta)^7-693\cos(\theta)^5+315\cos(\theta)^3-35\cos(\theta))\) | \(\frac{\sqrt{15}}{32\sqrt{\pi}}(429z^7-693z^5+315z^3-35z)\) | ||
| 8 | \(\frac{1}{128}(6435w^8-12012w^6+6930w^4-1260w^2+35)\) | \(\frac{\sqrt{17}}{2\sqrt{\pi}}(6435\cos(\theta)^8-12012\cos(\theta)^6+6930\cos(\theta)^4-1260\cos(\theta)^2+35)\) | \(\frac{\sqrt{17}}{256\sqrt{\pi}}(6435z^8-12012z^6+6930z^4-1260z^2+35)\) | ||
| 9 | \(\frac{1}{128}(12155w^9-25740w^7+18018w^5-4620w^3+315w)\) | \(\frac{\sqrt{19}}{2\sqrt{\pi}}(12155\cos(\theta)^9-25740\cos(\theta)^7+18018\cos(\theta)^5-4620\cos(\theta)^3+315\cos(\theta))\) | \(\frac{\sqrt{19}}{256\sqrt{\pi}}(12155z^9-25740z^7+18018z^5-4620z^3+315z)\) | ||
| 10 | \(\frac{1}{256}(46189w^{10}-109395w^8+90090w^6-30030w^4+3465w^2-63)\) | \(\frac{\sqrt{21}}{2\sqrt{\pi}}(46189\cos(\theta)^{10}-109395\cos(\theta)^8+90090\cos(\theta)^6-30030\cos(\theta)^4+3465\cos(\theta)^2-63)\) | \(\frac{\sqrt{21}}{512\sqrt{\pi}}(46189z^{10}-109395z^8+90090z^6-30030z^4+3465z^2-63)\) | ||
| 1 | \(\frac{1}{\sqrt{\pi}}\cos(\phi)\) | 1 | \((1-w^2)^{1/2}\) | \(\frac{\sqrt{3}}{2\sqrt{\pi}}\cos(\phi)\) | \(\frac{\sqrt{3}}{2\sqrt{\pi}}x\) |
| 2 | \(3w(1-w^2)^{1/2}\) | \(\frac{\sqrt{5}}{2\sqrt{3\pi}}\cos(\theta)\cos(\phi)\) | \(\frac{\sqrt{15}}{2\sqrt{\pi}}xz\) | ||
| 3 | \(\frac{3}{2}(5w^2-1)(1-w^2)^{1/2}\) | \(\frac{\sqrt{7}}{2\sqrt{6\pi}}(5\cos(\theta)^2-1)\cos(\phi)\) | \(\frac{\sqrt{21}}{4\sqrt{2\pi}}x(5z^2-1)\) | ||
| 4 | \(\frac{5}{2}(7w^3-3w)(1-w^2)^{1/2}\) | \(\frac{\sqrt{9}}{2\sqrt{10\pi}}(7\cos(\theta)^3-3\cos(\theta))\cos(\phi)\) | \(\frac{3\sqrt{5}}{4\sqrt{2\pi}}x(7z^3-3z)\) | ||
| 5 | \(\frac{15}{8}(21w^4-14w^2+1)(1-w^2)^{1/2}\) | \(\frac{\sqrt{11}}{2\sqrt{15\pi}}(21\cos(\theta)^4-14\cos(\theta)^2+1)\cos(\phi)\) | \(\frac{\sqrt{165}}{16\sqrt{\pi}}x(21z^4-14z^2+1)\) | ||
| 6 | \(\frac{21}{8}(33w^5-30w^3+5w)(1-w^2)^{1/2}\) | \(\frac{\sqrt{13}}{2\sqrt{21\pi}}(33\cos(\theta)^5-30\cos(\theta)^3+5\cos(\theta))\cos(\phi)\) | \(\frac{\sqrt{273}}{16\sqrt{\pi}}x(33z^5-30z^3+5z)\) | ||
| 7 | \(\frac{7}{16}(429w^6-495w^4+135w^2-5)(1-w^2)^{1/2}\) | \(\frac{\sqrt{15}}{4\sqrt{7\pi}}(429\cos(\theta)^6-495\cos(\theta)^4+135\cos(\theta)^2-5)\cos(\phi)\) | \(\frac{\sqrt{105}}{64\sqrt{\pi}}x(429z^6-495z^4+135z^2-5)\) | ||
| 8 | \(\frac{9}{16}(715w^7-1001w^5+385w^3-35w)(1-w^2)^{1/2}\) | \(\frac{\sqrt{17}}{12\sqrt{\pi}}(715\cos(\theta)^7-1001\cos(\theta)^5+385\cos(\theta)^3-35\cos(\theta))\cos(\phi)\) | \(\frac{3\sqrt{17}}{64\sqrt{\pi}}x(715z^7-1001z^5+385z^3-35z)\) | ||
| 9 | \(\frac{45}{128}(2431w^8-4004w^6+2002w^4-308w^2+7)(1-w^2)^{1/2}\) | \(\frac{\sqrt{19}}{6\sqrt{5\pi}}(2431\cos(\theta)^8-4004\cos(\theta)^6+2002\cos(\theta)^4-308\cos(\theta)^2+7)\cos(\phi)\) | \(\frac{3\sqrt{95}}{256\sqrt{\pi}}x(2431z^8-4004z^6+2002z^4-308z^2+7)\) | ||
| 10 | \(\frac{55}{128}(4199w^9-7956w^7+4914w^5-1092w^3+63w)(1-w^2)^{1/2}\) | \(\frac{\sqrt{21}}{2\sqrt{55\pi}}(4199\cos(\theta)^9-7956\cos(\theta)^7+4914\cos(\theta)^5-1092\cos(\theta)^3+63\cos(\theta))\cos(\phi)\) | \(\frac{\sqrt{1155}}{256\sqrt{\pi}}x(4199z^9-7956z^7+4914z^5-1092z^3+63z)\) | ||
| 2 | \(\frac{1}{\sqrt{\pi}}\cos(2\phi)\) | 2 | \(3(1-w^2)\) | \(\frac{\sqrt{5}}{4\sqrt{3\pi}}\cos(2\phi)\) | \(\frac{\sqrt{15}}{4\sqrt{\pi}}(x^2-y^2)\) |
| 3 | \(15w(1-w^2)\) | \(\frac{\sqrt{7}}{4\sqrt{15\pi}}\cos(\theta)\cos(2\phi)\) | \(\frac{\sqrt{105}}{4\sqrt{\pi}}(x^2-y^2)z\) | ||
| 4 | \(\frac{15}{2}(7w^2-1)(1-w^2)\) | \(\frac{\sqrt{9}}{12\sqrt{5\pi}}(7\cos(\theta)^2-1)\cos(2\phi)\) | \(\frac{3\sqrt{5}}{8\sqrt{\pi}}(x^2-y^2)(7z^2-1)\) | ||
| 5 | \(\frac{105}{2}(3w^3-w)(1-w^2)\) | \(\frac{\sqrt{11}}{4\sqrt{105\pi}}(3\cos(\theta)^3-\cos(\theta))\cos(2\phi)\) | \(\frac{\sqrt{1155}}{8\sqrt{\pi}}(x^2-y^2)(3z^3-z)\) | ||
| 6 | \(\frac{105}{8}(33w^4-18w^2+1)(1-w^2)\) | \(\frac{\sqrt{13}}{4\sqrt{210\pi}}(33\cos(\theta)^4-18\cos(\theta)^2+1)\cos(2\phi)\) | \(\frac{\sqrt{1365}}{32\sqrt{2\pi}}(x^2-y^2)(33z^4-18z^2+1)\) | ||
| 7 | \(\frac{63}{8}(143w^5-110w^3+15w)(1-w^2)\) | \(\frac{\sqrt{15}}{12\sqrt{14\pi}}(143\cos(\theta)^5-110\cos(\theta)^3+15\cos(\theta))\cos(2\phi)\) | \(\frac{3\sqrt{105}}{32\sqrt{2\pi}}(x^2-y^2)(143z^5-110z^3+15z)\) | ||
| 8 | \(\frac{315}{16}(143w^6-143w^4+33w^2-1)(1-w^2)\) | \(\frac{\sqrt{17}}{12\sqrt{70\pi}}(143\cos(\theta)^6-143\cos(\theta)^4+33\cos(\theta)^2-1)\cos(2\phi)\) | \(\frac{3\sqrt{595}}{64\sqrt{2\pi}}(x^2-y^2)(143z^6-143z^4+33z^2-1)\) | ||
| 9 | \(\frac{495}{16}(221w^7-273w^5+91w^3-7w)(1-w^2)\) | \(\frac{\sqrt{19}}{12\sqrt{110\pi}}(221\cos(\theta)^7-273\cos(\theta)^5+91\cos(\theta)^3-7\cos(\theta))\cos(2\phi)\) | \(\frac{3\sqrt{1045}}{64\sqrt{2\pi}}(x^2-y^2)(221z^7-273z^5+91z^3-7z)\) | ||
| 10 | \(\frac{495}{128}(4199w^8-6188w^6+2730w^4-364w^2+7)(1-w^2)\) | \(\frac{\sqrt{21}}{12\sqrt{55\pi}}(4199\cos(\theta)^8-6188\cos(\theta)^6+2730\cos(\theta)^4-364\cos(\theta)^2+7)\cos(2\phi)\) | \(\frac{3\sqrt{1155}}{512\sqrt{\pi}}(x^2-y^2)(4199z^8-6188z^6+2730z^4-364z^2+7)\) | ||
| 3 | \(\frac{1}{\sqrt{\pi}}\cos(3\phi)\) | 3 | \(15(1-w^2)^{3/2}\) | \(\frac{\sqrt{7}}{12\sqrt{10\pi}}\cos(3\phi)\) | \(\frac{\sqrt{35}}{4\sqrt{2\pi}}(x^3-3xy^2)\) |
| 4 | \(105w(1-w^2)^{3/2}\) | \(\frac{\sqrt{9}}{12\sqrt{70\pi}}\cos(\theta)\cos(3\phi)\) | \(\frac{3\sqrt{35}}{4\sqrt{2\pi}}(x^3-3xy^2)z\) | ||
| 5 | \(\frac{105}{2}(9w^2-1)(1-w^2)^{3/2}\) | \(\frac{\sqrt{11}}{24\sqrt{70\pi}}(9\cos(\theta)^2-1)\cos(3\phi)\) | \(\frac{\sqrt{385}}{16\sqrt{2\pi}}(x^3-3xy^2)(9z^2-1)\) | ||
| 6 | \(\frac{315}{2}(11w^3-3w)(1-w^2)^{3/2}\) | \(\frac{\sqrt{13}}{24\sqrt{210\pi}}(11\cos(\theta)^3-3\cos(\theta))\cos(3\phi)\) | \(\frac{\sqrt{1365}}{16\sqrt{2\pi}}(x^3-3xy^2)(11z^3-3z)\) | ||
| 7 | \(\frac{315}{8}(143w^4-66w^2+3)(1-w^2)^{3/2}\) | \(\frac{\sqrt{15}}{120\sqrt{7\pi}}(143\cos(\theta)^4-66\cos(\theta)^2+3)\cos(3\phi)\) | \(\frac{3\sqrt{105}}{64\sqrt{\pi}}(x^3-3xy^2)(143z^4-66z^2+3)\) | ||
| 8 | \(\frac{3465}{8}(39w^5-26w^3+3w)(1-w^2)^{3/2}\) | \(\frac{\sqrt{17}}{24\sqrt{1155\pi}}(39\cos(\theta)^5-26\cos(\theta)^3+3\cos(\theta))\cos(3\phi)\) | \(\frac{\sqrt{19635}}{64\sqrt{\pi}}(x^3-3xy^2)(39z^5-26z^3+3z)\) | ||
| 9 | \(\frac{3465}{16}(221w^6-195w^4+39w^2-1)(1-w^2)^{3/2}\) | \(\frac{\sqrt{19}}{24\sqrt{2310\pi}}(221\cos(\theta)^6-195\cos(\theta)^4+39\cos(\theta)^2-1)\cos(3\phi)\) | \(\frac{\sqrt{21945}}{128\sqrt{2\pi}}(x^3-3xy^2)(221z^6-195z^4+39z^2-1)\) | ||
| 10 | \(\frac{6435}{16}(323w^7-357w^5+105w^3-7w)(1-w^2)^{3/2}\) | \(\frac{\sqrt{21}}{24\sqrt{1430\pi}}(323\cos(\theta)^7-357\cos(\theta)^5+105\cos(\theta)^3-7\cos(\theta))\cos(3\phi)\) | \(\frac{3\sqrt{15015}}{128\sqrt{2\pi}}(x^3-3xy^2)(323z^7-357z^5+105z^3-7z)\) | ||
| 4 | \(\frac{1}{\sqrt{\pi}}\cos(4\phi)\) | 4 | \(105(1-w^2)^2\) | \(\frac{\sqrt{9}}{48\sqrt{35\pi}}\cos(4\phi)\) | \(\frac{3\sqrt{35}}{16\sqrt{\pi}}(x^4-6x^2y^2+y^4)\) |
| 5 | \(945w(1-w^2)^2\) | \(\frac{\sqrt{11}}{144\sqrt{35\pi}}\cos(\theta)\cos(4\phi)\) | \(\frac{3\sqrt{385}}{16\sqrt{\pi}}(x^4-6x^2y^2+y^4)z\) | ||
| 6 | \(\frac{945}{2}(11w^2-1)(1-w^2)^2\) | \(\frac{\sqrt{13}}{720\sqrt{7\pi}}(11\cos(\theta)^2-1)\cos(4\phi)\) | \(\frac{3\sqrt{91}}{32\sqrt{\pi}}(x^4-6x^2y^2+y^4)(11z^2-1)\) | ||
| 7 | \(\frac{3465}{2}(13w^3-3w)(1-w^2)^2\) | \(\frac{\sqrt{15}}{240\sqrt{77\pi}}(13\cos(\theta)^3-3\cos(\theta))\cos(4\phi)\) | \(\frac{3\sqrt{1155}}{32\sqrt{\pi}}(x^4-6x^2y^2+y^4)(13z^3-3z)\) | ||
| 8 | \(\frac{10395}{8}(65w^4-26w^2+1)(1-w^2)^2\) | \(\frac{\sqrt{17}}{720\sqrt{77\pi}}(65\cos(\theta)^4-26\cos(\theta)^2+1)\cos(4\phi)\) | \(\frac{3\sqrt{1309}}{128\sqrt{\pi}}(x^4-6x^2y^2+y^4)(65z^4-26z^2+1)\) | ||
| 9 | \(\frac{135135}{8}(17w^5-10w^3+w)(1-w^2)^2\) | \(\frac{\sqrt{19}}{144\sqrt{5005\pi}}(17\cos(\theta)^5-10\cos(\theta)^3+\cos(\theta))\cos(4\phi)\) | \(\frac{3\sqrt{95095}}{128\sqrt{\pi}}(x^4-6x^2y^2+y^4)(17z^5-10z^3+z)\) | ||
| 10 | \(\frac{45045}{16}(323w^6-255w^4+45w^2-1)(1-w^2)^2\) | \(\frac{\sqrt{21}}{336\sqrt{715\pi}}(323\cos(\theta)^6-255\cos(\theta)^4+45\cos(\theta)^2-1)\cos(4\phi)\) | \(\frac{3\sqrt{15015}}{256\sqrt{\pi}}(x^4-6x^2y^2+y^4)(323z^6-255z^4+45z^2-1)\) | ||
| 5 | \(\frac{1}{\sqrt{\pi}}\cos(5\phi)\) | 5 | \(945(1-w^2)^{5/2}\) | \(\frac{\sqrt{11}}{720\sqrt{14\pi}}\cos(5\phi)\) | \(\frac{3\sqrt{77}}{16\sqrt{2\pi}}(x^5-10x^3y^2+5xy^4)\) |
| 6 | \(10395w(1-w^2)^{5/2}\) | \(\frac{\sqrt{13}}{720\sqrt{154\pi}}\cos(\theta)\cos(5\phi)\) | \(\frac{3\sqrt{1001}}{16\sqrt{2\pi}}(x^5-10x^3y^2+5xy^4)z\) | ||
| 7 | \(\frac{10395}{2}(13w^2-1)(1-w^2)^{5/2}\) | \(\frac{\sqrt{15}}{1440\sqrt{77\pi}}(13\cos(\theta)^2-1)\cos(5\phi)\) | \(\frac{3\sqrt{1155}}{64\sqrt{\pi}}(x^5-10x^3y^2+5xy^4)(13z^2-1)\) | ||
| 8 | \(\frac{135135}{2}(5w^3-w)(1-w^2)^{5/2}\) | \(\frac{\sqrt{17}}{1440\sqrt{1001\pi}}(5\cos(\theta)^3-\cos(\theta))\cos(5\phi)\) | \(\frac{3\sqrt{17017}}{64\sqrt{\pi}}(x^5-10x^3y^2+5xy^4)(5z^3-z)\) | ||
| 9 | \(\frac{135135}{8}(85w^4-30w^2+1)(1-w^2)^{5/2}\) | \(\frac{\sqrt{19}}{5040\sqrt{286\pi}}(85\cos(\theta)^4-30\cos(\theta)^2+1)\cos(5\phi)\) | \(\frac{3\sqrt{2717}}{128\sqrt{2\pi}}(x^5-10x^3y^2+5xy^4)(85z^4-30z^2+1)\) | ||
| 10 | \(\frac{135135}{8}(323w^5-170w^3+15w)(1-w^2)^{5/2}\) | \(\frac{\sqrt{21}}{5040\sqrt{286\pi}}(323\cos(\theta)^5-170\cos(\theta)^3+15\cos(\theta))\cos(5\phi)\) | \(\frac{3\sqrt{3003}}{128\sqrt{2\pi}}(x^5-10x^3y^2+5xy^4)(323z^5-170z^3+15z)\) | ||
| 6 | \(\frac{1}{\sqrt{\pi}}\cos(6\phi)\) | 6 | \(10395(1-w^2)^3\) | \(\frac{\sqrt{13}}{1440\sqrt{462\pi}}\cos(6\phi)\) | \(\frac{\sqrt{3003}}{32\sqrt{2\pi}}(x^6-15x^4y^2+15x^2y^4-y^6)\) |
| 7 | \(135135w(1-w^2)^3\) | \(\frac{\sqrt{15}}{1440\sqrt{2002\pi}}\cos(\theta)\cos(6\phi)\) | \(\frac{3\sqrt{15015}}{32\sqrt{2\pi}}(x^6-15x^4y^2+15x^2y^4-y^6)z\) | ||
| 8 | \(\frac{135135}{2}(15w^2-1)(1-w^2)^3\) | \(\frac{\sqrt{17}}{10080\sqrt{858\pi}}(15\cos(\theta)^2-1)\cos(6\phi)\) | \(\frac{\sqrt{7293}}{64\sqrt{2\pi}}(x^6-15x^4y^2+15x^2y^4-y^6)(15z^2-1)\) | ||
| 9 | \(\frac{675675}{2}(17w^3-3w)(1-w^2)^3\) | \(\frac{\sqrt{19}}{10080\sqrt{4290\pi}}(17\cos(\theta)^3-3\cos(\theta))\cos(6\phi)\) | \(\frac{\sqrt{40755}}{64\sqrt{2\pi}}(x^6-15x^4y^2+15x^2y^4-y^6)(17z^3-3z)\) | ||
| 10 | \(\frac{675675}{8}(323w^4-102w^2+3)(1-w^2)^3\) | \(\frac{\sqrt{21}}{20160\sqrt{1430\pi}}(323\cos(\theta)^4-102\cos(\theta)^2+3)\cos(6\phi)\) | \(\frac{3\sqrt{15015}}{512\sqrt{2\pi}}(x^6-15x^4y^2+15x^2y^4-y^6)(323z^4-102z^2+3)\) | ||
| 7 | \(\frac{1}{\sqrt{\pi}}\cos(7\phi)\) | 7 | \(135135(1-w^2)^{7/2}\) | \(\frac{\sqrt{15}}{20160\sqrt{143\pi}}\cos(7\phi)\) | \(\frac{3\sqrt{2145}}{64\sqrt{\pi}}(x^7-21x^5y^2+35x^3y^4-7xy^6)\) |
| 8 | \(2027025w(1-w^2)^{7/2}\) | \(\frac{\sqrt{17}}{60480\sqrt{715\pi}}\cos(\theta)\cos(7\phi)\) | \(\frac{3\sqrt{12155}}{64\sqrt{\pi}}(x^7-21x^5y^2+35x^3y^4-7xy^6)z\) | ||
| 9 | \(\frac{2027025}{2}(17w^2-1)(1-w^2)^{7/2}\) | \(\frac{\sqrt{19}}{120960\sqrt{1430\pi}}(17\cos(\theta)^2-1)\cos(7\phi)\) | \(\frac{3\sqrt{13585}}{256\sqrt{2\pi}}(x^7-21x^5y^2+35x^3y^4-7xy^6)(17z^2-1)\) | ||
| 10 | \(\frac{11486475}{2}(19w^3-3w)(1-w^2)^{7/2}\) | \(\frac{\sqrt{21}}{40320\sqrt{24310\pi}}(19\cos(\theta)^3-3\cos(\theta))\cos(7\phi)\) | \(\frac{3\sqrt{255255}}{256\sqrt{2\pi}}(x^7-21x^5y^2+35x^3y^4-7xy^6)(19z^3-3z)\) | ||
| 8 | \(\frac{1}{\sqrt{\pi}}\cos(8\phi)\) | 8 | \(2027025(1-w^2)^4\) | \(\frac{\sqrt{17}}{241920\sqrt{715\pi}}\cos(8\phi)\) | \(\frac{3\sqrt{12155}}{256\sqrt{\pi}}(x^8-28x^6y^2+70x^4y^4-28x^2y^6+y^8)\) |
| 9 | \(34459425w(1-w^2)^4\) | \(\frac{\sqrt{19}}{241920\sqrt{12155\pi}}\cos(\theta)\cos(8\phi)\) | \(\frac{3\sqrt{230945}}{256\sqrt{\pi}}(x^8-28x^6y^2+70x^4y^4-28x^2y^6+y^8)z\) | ||
| 10 | \(\frac{34459425}{2}(19w^2-1)(1-w^2)^4\) | \(\frac{\sqrt{21}}{725760\sqrt{12155\pi}}(19\cos(\theta)^2-1)\cos(8\phi)\) | \(\frac{\sqrt{255255}}{512\sqrt{\pi}}(x^8-28x^6y^2+70x^4y^4-28x^2y^6+y^8)(19z^2-1)\) | ||
| 9 | \(\frac{1}{\sqrt{\pi}}\cos(9\phi)\) | 9 | \(34459425(1-w^2)^{9/2}\) | \(\frac{\sqrt{19}}{725760\sqrt{24310\pi}}\cos(9\phi)\) | \(\frac{\sqrt{230945}}{256\sqrt{2\pi}}(x^9-36x^7y^2+126x^5y^4-84x^3y^6+9xy^8)\) |
| 10 | \(654729075w(1-w^2)^{9/2}\) | \(\frac{\sqrt{21}}{725760\sqrt{461890\pi}}\cos(\theta)\cos(9\phi)\) | \(\frac{\sqrt{4849845}}{256\sqrt{2\pi}}(x^9-36x^7y^2+126x^5y^4-84x^3y^6+9xy^8)z\) | ||
| 10 | \(\frac{1}{\sqrt{\pi}}\cos(10\phi)\) | 10 | \(654729075(1-w^2)^5\) | \(\frac{\sqrt{21}}{7257600\sqrt{92378\pi}}\cos(10\phi)\) | \(\frac{\sqrt{969969}}{512\sqrt{2\pi}}(x^{10}-45x^8y^2+210x^6y^4-210x^4y^6+45x^2y^8-y^{10})\) |
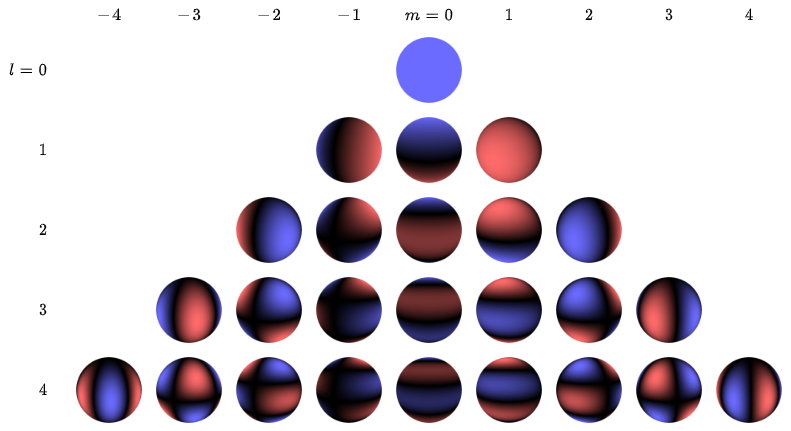
\(l=4\)までの球面調和関数 (青が正の値、赤が負の値を表す)
例
実際の画像に対して球面調和関数による近似を実行した結果を掲載する。(元の画像)
左上から\(L=0, 5, 10, 20, 30, 50, 85\)と元の画像で、それぞれパラメーターの数は\(1, 36, 121, 441, 961, 2601, 7396, \infty\)である。







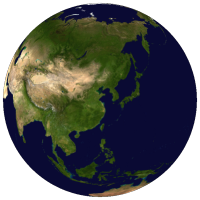
球面調和関数による近似