高速逆平方根
目次
高速逆平方根
高速逆平方根(fast inverse square root)は、1980年代に考案された平方根の逆数\(\frac{1}{\sqrt{x}}\)を高速に求めるアルゴリズム。1999年にMac OS用のFPSゲーム「Quake III Arena」に実装されたことをきっかけに有名になり、ベクトルを正規化する目的で3D技術に転用されるなどした。
しかしその後、CPUやGPUなどのハードウェアの性能向上によって逆平方根の専用命令が標準搭載されるようになり、現在ではこのアルゴリズムを使う利点はなくなっている。
このように既に過去の遺物となったこのアルゴリズムだが、仕組みが面白いので詳しく見てみる。
ソースコード
Quake III Arenaに実装された高速逆平方根のソースコードを抜粋する。言語はC言語。(見やすさのために一部整形してある)
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}
type punningによる逆平方根の近似
ソースコードの前半ではtype punningによって、ある値\(y\)とその対数\(i\)との相互変換を近似的に行っている。
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
iは整数でyは実数。
上記抜粋部分の1行目では、&yによってyのポインタを取得し、ポインタの型をfloat*からlong*にキャストし、最後に*でポインタが指す値を取得してiに代入している。
つまり、実数として格納されたビット列を強制的に整数として読み取っている。このようにあるデータを異なるデータ型として再解釈することをtype punningと言う。
データ型の仕様
long型
long型 (32-bit) の構造は下図のようになっている。
ビット列は符号\(s\)と残りの部分\(v\)によって構成される。

long型の構造
ビット列が指す値\(x\)は次のように定義される。
| 条件 | 値 | 備考 |
|---|---|---|
| \(s=0\) | \(x=v\) | |
| \(s=1\) | \(x=v-2^{31}\) | 2の補数と呼ばれる計算法 |
したがって、long型では\(-2^{31}=-2147483648\)から\(2^{31}-1=2147483647\)までの全ての整数が次の表のように表現されることになる。
| ビット列 | 値 |
|---|---|
| 0 0000000000000000000000000000000 | 0 |
| 0 0000000000000000000000000000001 | 1 |
| 0 0000000000000000000000000000010 | 2 |
| ︙ | ︙ |
| 0 1111111111111111111111111111110 | 2147483646 |
| 0 1111111111111111111111111111111 | 2147483647 |
| 1 0000000000000000000000000000000 | -2147483648 |
| 1 0000000000000000000000000000001 | -2147483647 |
| ︙ | ︙ |
| 1 1111111111111111111111111111110 | -2 |
| 1 1111111111111111111111111111111 | -1 |
float型
float型 (32-bit) の構造は下図のようになっている。(IEEE 754の仕様に基づく)
ビット列は符号\(s\) (sign)、指数\(e\) (exponent)、仮数\(m\) (mantissa)によって構成される。

float型の構造
ビット列が指す値\(x\)は次のように定義される。
| 条件1 | 条件2 | 値 | 備考 |
|---|---|---|---|
| \(e\)の全ビットが1 | \(m\)の全ビットが0 | \(x=(-1)^s\cdot\infty\) | |
| それ以外 | \(x=\mathrm{NaN}\) | ||
| \(e\)の全ビットが0 | \(x=(-1)^s\cdot \left(0+\frac{m}{2^{23}}\right)\cdot2^{1-127}\) | 非正規化数と呼ぶ | |
| それ以外 | \(x=(-1)^s\cdot \left(1+\frac{m}{2^{23}}\right)\cdot2^{e-127}\) | ||
\(e\)の値を固定すると、\(x\)は
\begin{align*} 2^{e-127} \leq x < 2^{e-126} \end{align*}
の範囲の値を等間隔に取ることになる。(符号が\(s=0\)の場合)
ただし、\(e=0\)のときにも\(2^{-127} \leq x < 2^{-126}\)としてしまうと\([0, 2^{-127})\)の区間の値を表現する方法がなくなってしまう。そこで、\(e\)の全ビットが0のときは非正規化数と呼ばれる特殊な定義を行い、\(x=0\)から\(x=2^{-126}\)までを等間隔に表現できるようにしている。
したがって、float型では\(-16777215\times2^{104}=-(2^{128}-2^{104})\)から\(16777215\times2^{104}=2^{128}-2^{104}\)までの実数(有理数)の一部が次の表のように表現されることになる。
| ビット列 | 値 | 備考 |
|---|---|---|
| 0 00000000 00000000000000000000000 | \(+0\) | 非正規化数 |
| 0 00000000 00000000000000000000001 | \(1\times2^{-149}\) | 非正規化数 |
| 0 00000000 00000000000000000000010 | \(2\times2^{-149}\) | 非正規化数 |
| ︙ | ︙ | 非正規化数 |
| 0 00000000 11111111111111111111111 | \(8388607\times2^{-149}\) | 非正規化数 |
| 0 00000001 00000000000000000000000 | \(8388608\times2^{-149} = 2^{-126}\) | |
| ︙ | ︙ | |
| 0 00000001 11111111111111111111111 | \(16777215\times2^{-149}\) | |
| 0 00000010 00000000000000000000000 | \(8388608\times2^{-148} = 2^{-125}\) | |
| ︙ | ︙ | |
| 0 11111110 11111111111111111111111 | \(16777215\times2^{104}\) | |
| 0 11111111 00000000000000000000000 | \(+\infty\) | 無限大 |
| 0 11111111 00000000000000000000001 | NaN | |
| 0 11111111 00000000000000000000010 | NaN | |
| ︙ | ︙ | |
| 0 11111111 11111111111111111111111 | NaN | |
| 1 00000000 00000000000000000000000 | \(-0\) | 非正規化数 負の0 |
| 1 00000000 00000000000000000000001 | \(-1\times2^{-149}\) | 非正規化数 |
| ︙ | ︙ | |
| 1 11111110 11111111111111111111111 | \(-16777215\times2^{104}\) | |
| 1 11111111 00000000000000000000000 | \(-\infty\) | 無限大 |
| 1 11111111 00000000000000000000001 | NaN | |
| ︙ | ︙ | |
| 1 11111111 11111111111111111111111 | NaN |
type punning
これ以降は非正規化数・無限大・NaNではない通常の数値に限定して話を進める。また、符号は正(\(s=0\))とする。
ビット列の(下位ビットから)30-23ビット目が指す値を\(e\)、22-0ビット目が指す値を\(m\)とする。
このとき、このビット列をlong型として読み取った値\(i\)と、float型として読み取った値\(y\)は次のようになる。ただし\(s=0\)とし、\(y\)は非正規化数・無限大・NaNではないものとする。
\begin{align*} i &= e\cdot2^{23} + m \\ y &= \left(1+\frac{m}{2^{23}}\right)\cdot2^{e-127} \end{align*}
\(m\)は\(0\leq m\leq2^{23}-1\)の値を取るので、
\begin{align*} 1 \leq 1+\frac{m}{2^{23}} < 2 \end{align*}
\begin{align*} 2^{e-127} \leq y = \left(1+\frac{m}{2^{23}}\right)\cdot2^{e-127} < 2^{e-126} \end{align*}
\begin{align*} e \leq \log_2 y + 127 < e + 1 \end{align*}
となり、\(e\)の値を
\begin{align*} e = \lfloor\log_2 y\rfloor + 127 \end{align*}
と特定することができる。
また、\(e\)を用いて\(m\)の値も
\begin{align*} m &= \left(y\cdot2^{127-e} - 1\right)\cdot2^{23} \\ &= \left(y\cdot2^{-\lfloor\log_2 y\rfloor} - 1\right)\cdot2^{23} \\ \end{align*}
と計算することができる。
これらを用いると、\(i\)は次のように表すことができる。
\begin{align*} i &= e\cdot2^{23} + m \\ &= \left(\lfloor\log_2 y\rfloor + 127\right)\cdot2^{23} + \left(y\cdot2^{-\lfloor\log_2 y\rfloor} - 1\right)\cdot2^{23} \\ &= \left(\lfloor\log_2 y\rfloor + y\cdot2^{-\lfloor\log_2 y\rfloor} + 126\right)\cdot2^{23} \\ \end{align*}
これを\(i=f(y)\)と表すことにする。
\begin{align*} i &= f(y) \\ &= \left(\lfloor\log_2 y\rfloor + y\cdot2^{-\lfloor\log_2 y\rfloor} + 126\right)\cdot2^{23} \\ \end{align*}
特に、\(y=2^n\)となるような\(n\)が存在するときは\(\lfloor\log_2 y\rfloor=\log_2 y\)となるので、
\begin{align*} f(y) &= \left(\lfloor\log_2 y\rfloor + y\cdot2^{-\lfloor\log_2 y\rfloor} + 126\right)\cdot2^{23} \\ &= \left(\log_2 y + y\cdot2^{-\log_2 y} + 126\right)\cdot2^{23} \\ &= \left(\log_2 y + 1 + 126\right)\cdot2^{23} \\ &= \left(\log_2 y + 127\right)\cdot2^{23} \\ \end{align*}
となり、\(y\)の対数関数で表すことができる。
また、\(2^n\leq y<2^{n+1}\)のときは、
\begin{align*} f(y) &= \left(\lfloor\log_2 y\rfloor + y\cdot2^{-\lfloor\log_2 y\rfloor} + 126\right)\cdot2^{23} \\ &= \left(n + y\cdot2^{-n} + 126\right)\cdot2^{23} \\ \end{align*}
となり、\(y\)に関して一次関数になる。
したがって、\(f(y)\)は対数関数を区分的に線形補間した関数になっていることがわかる。この関係を下図に示す。
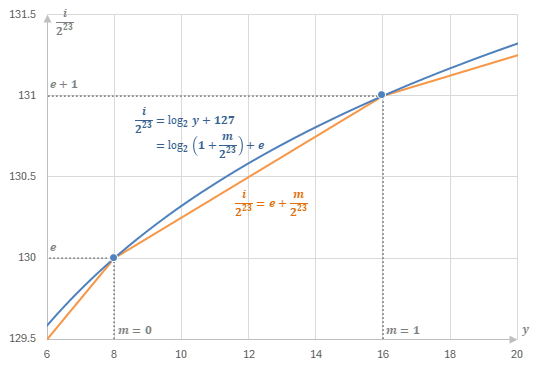
type punningによる対数関数の近似 (青が対数関数で、橙がその線形補間)
つまり、\(y\)をfloat型からlong型にpunningしたとき、\(i=f(y)\)(上図の橙線)に従って値が変換されることになる。
逆にlong型からfloat型へのpunningはこの逆関数によって変換される。(つまり指数関数の線形補間)
\(f(y)\)の対数関数の床関数を取る部分が、ほぼ対数関数になっていると考えると次のように表すことができる。
\begin{align*} f(y) &= \left(\lfloor\log_2 y\rfloor + y\cdot2^{-\lfloor\log_2 y\rfloor} + 126\right)\cdot2^{23} \\ &\sim \left(\log_2 y + y\cdot2^{-\log_2 y} + 126\right)\cdot2^{23} \\ &= \left(\log_2 y + 127\right)\cdot2^{23} \\ \end{align*}
このとき、\(f\)の逆関数(long型からfloat型へのpunning)は、
\begin{align*} f^{-1}(i) \sim 2^{\frac{i}{2^{23}}-127} \end{align*}
と表される。
逆平方根
\(g(y) = f^{-1}(a\cdot2^{23} + bf(y))\)という変換を考える。
(高速逆平方根の実装では、\(a\cdot 2^{23}\)が定数0x5f3759dfに相当し、\(b\)を掛ける部分が右シフトに相当する)
\begin{align*} g(y) &= f^{-1}(a\cdot2^{23} + bf(y)) \\ &\sim f^{-1}\left(a\cdot2^{23} + b\left(\log_2 y + 127\right)\cdot2^{23}\right) \\ &= f^{-1}\left(\left(a + b\left(\log_2 y + 127\right)\right)\cdot2^{23}\right) \\ &\sim 2^{a + b\left(\log_2 y + 127\right)-127} \\ &= 2^{a + 127(b-1)}y^b \\ \end{align*}
となるので、
\begin{align*} a = -127(b-1) \end{align*}
とすれば、
\begin{align*} g(y) &\sim y^b \\ \end{align*}
となり、この変換によって\(y\)の実数乗を計算することができる。
特に\(b=-\frac{1}{2}\)とすることで、逆平方根
\begin{align*} g(y) &\sim y^{-1/2} \\ &= \frac{1}{\sqrt{y}} \\ \end{align*}
を計算できる。
\(b=-\frac{1}{2}\)を代入すると\(a=-127\left(-\frac{1}{2}-1\right)=\frac{3\cdot127}{2}\)となるので、
\begin{align*} a\cdot2^{23} + bf(y) &= \frac{3\cdot127}{2}\cdot2^{23} - \frac{f(y)}{2} \\ &= 381\cdot2^{22} - \frac{f(y)}{2} \\ &= 1598029824 - \frac{f(y)}{2} \\ \end{align*}
となる。
\(1598029824\)は16進数で表すと「0x5F400000」であり、ソースコードに現れる「0x5F3759DF」という値と酷似ししている。また、\(f(y)\)を2で割る操作は整数では右シフトで実装できる(余りは切り捨てられる)。
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
まとめると、ソースコードのこの3行は
- 1行目で\(f(y)\)を実行
- 2行目で\(a + bf(y)\)を実行
- 3行目で\(f^{-1}(a + bf(y))\)を実行
することによって逆平方根\(\frac{1}{\sqrt{y}}\)を実行していると理解することができる。
「0x5F400000」と「0x5F3759DF」の微妙なズレは、\(f(y)\)が実際には対数関数そのものではないことに起因する誤差を修正するためのものである。(後述)
具体的に「0x5F3759DF」が選ばれた由来はよくわかっていないようで、実装によっては異なる値が使われることもある。
Newton法
これまでの手順で逆平方根\(\frac{1}{\sqrt{y}}\)にかなり近い値を得ることができた。
ソースコードの後半ではNewton法を用いて更に近似の精度を向上させている。
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
逆平方根\(y=\frac{1}{\sqrt{x}}\)は、関数\(F(y)=\frac{1}{y^2}-x\)の根と捉えることもできる。
したがって、Newton法によってより近い値を取ることができる。
\(F(x)\)微分可能な関数とし、その根を\(x^\ast\)とする。
\(x_0\)を任意に取る。
\(x_n\)が与えられたとき、座標\((x_n, F(x_n))\)における接線を考え、接線がグラフのx軸と交わる点のx座標を\(x_{n+1}\)とする。つまり、
\begin{align*} x_{n+1} = x_n - \frac{F(x_n)}{F'(x_n)} \end{align*}
とする。
このとき、\(x^\ast<x_n, F(x_n)>0\)で、区間\([x^\ast, x_n]\)において\(F\)が下に凸ならば、
\begin{align*} F'(x_n) &> \frac{F(x_n)-F(x^\ast)}{x_n-x^\ast} \\ &= \frac{F(x_n)}{x_n-x^\ast} \\ \end{align*}
なので、
\begin{align*} x_{n+1} &= x_n - \frac{F(x_n)}{F'(x_n)} \\ &< x_n - 0 \\ &= x_n \end{align*}
\begin{align*} x_{n+1} &= x_n - \frac{F(x_n)}{F'(x_n)} \\ &> x_n - (x_n - x^\ast) \\ &= x^\ast \end{align*}
となることから、\(x^\ast < x_{n+1} < x_n\)となり、\(x_n\)は何らかの値に収束すると言える。
また、\(x_n\)が\(x\)に収束するなら、
\begin{align*} x = x - \frac{F(x)}{F'(x)} \end{align*}
となるので、\(F(x)=0\)になるしかなく、\(x_n\)は\(x^\ast\)に収束することがわかる。
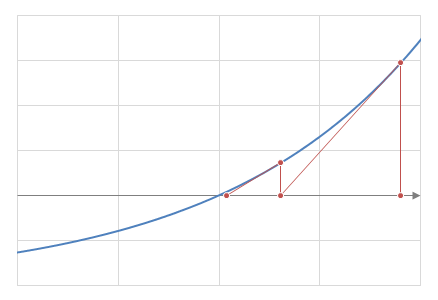
Newton法
また、\(x_n<x^\ast, F(x_n)<0\)で、区間\([x_n, x_{n+1}]\)において\(F\)が下に凸ならば、
\begin{align*} F'(x_n) &< \frac{F(x^\ast)-F(x_n)}{x^\ast-x_n} \\ &= -\frac{F(x_n)}{x^\ast-x_n} \\ \end{align*}
なので、
\begin{align*} x_{n+1} &= x_n - \frac{F(x_n)}{F'(x_n)} \\ &> x_n - (x_n - x^\ast) \\ &= x^\ast \end{align*}
となり、それ以降は\(x^\ast<x_n, F(x_n)>0\)の場合と同様。
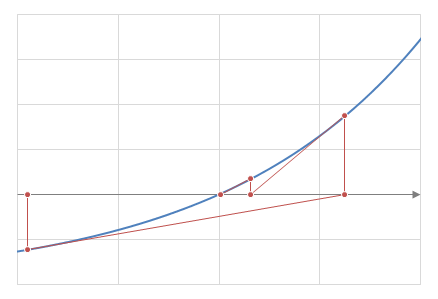
Newton法
これらを上下左右反転させた場合も同様に考えることができ、これによって\(F(x)\)が上に凸・下に凸、\(F(x)\)が単調増加・単調減少、\(x_n<x^\ast, x^\ast<x_m\)の組み合わせを全パターン網羅することができる。
したがって、\(x_n\)が\(x^\ast\)に十分近いとき(=考えるべき\(x\)の範囲で\(F(x)\)が常に一方に凸であると言えるとき)、\(x_n\)は根\(x^\ast\)に収束すると言える。
関数\(F(y)=\frac{1}{y^2}-x\)にNewton法を適用すると、
\begin{align*} y_{n+1} &= y_n - \frac{F(y_n)}{F'(y_n)} \\ &= y_n - \frac{\frac{1}{y_n^2}-x}{-2\frac{1}{y_n^3}} \\ &= y_n + \frac{(1-xy_n^2)y_n}{2} \\ &= y_n\left( \frac{3}{2} - \frac{x}{2}y_n^2\right) \\ \end{align*}
となりソースコードの記述と一致する。
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
近似の精度
近似値と真の逆平方根の比
\(y\)は\(e,m\)を用いて、
\begin{align*} y = \left(1 + \frac{m}{2^{23}}\right)\cdot2^{e-127} \\ \end{align*}
と表すことができることを既に確かめた。したがって、真の逆平方根は次のような値になる。
\begin{align*} \frac{1}{\sqrt{y}} = \frac{2^{(-e+127)/2}}{\sqrt{1 + \frac{m}{2^{23}}}} \\ \end{align*}
これに対して\(\frac{1}{\sqrt{y}}\)の近似値\(g(y)\)はどのような値を取るだろうか。
C言語による実装により忠実になるように、関数\(g(y)\)を改めて定義する。
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
\(1\leq c<2^{22}\)を用いて2行目の定数を\(381\cdot2^{22} - c\)と表すことにする。
また、右シフトが厳密には\(\frac{f(y)}{2}\)ではなく\(\left\lfloor\frac{f(y)}{2}\right\rfloor\)であることに注意する。
\begin{align*} g(y) &= f^{-1}\left(381\cdot2^{22} - c - \left\lfloor\frac{f(y)}{2}\right\rfloor\right) \\ &= f^{-1}\left(381\cdot2^{22} - c - \left\lfloor\frac{e\cdot2^{23}+m}{2}\right\rfloor\right) \\ &= f^{-1}\left((381 - e)\cdot2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ \end{align*}
ここで、\(e\)が奇数のときと偶数のときで分岐する。
\(e\)が奇数のとき
\(e\)が奇数\(e=2n+1\)のとき、
\begin{align*} g(y) &= f^{-1}\left((381 - e)\cdot2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ &= f^{-1}\left(\left(381 - 2n - 1\right)\cdot2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ &= f^{-1}\left(\left(190 - n\right)\cdot2^{23} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ &= f^{-1}\left(\left(189 - n\right)\cdot2^{23} + 2^{23} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ \end{align*}
\(1\leq c+\left\lfloor\frac{m}{2}\right\rfloor<2^{23}\)なので、\(0<2^{23} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)<2^{23}\)が成り立ち、\(f^{-1}\)の引数は
- 上位8-bit: \(189 - n\)
- 下位23-bit: \(2^{23} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\)
となることがわかる。
したがってtype punningによって再びfloat型に戻すと、
\begin{align*} g(y) &= f^{-1}\left(\left(189 - n\right)\cdot2^{23} + 2^{23} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ &= \left( 1 + \frac{2^{23} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)}{2^{23}} \right)\cdot2^{189 - n -127} \\ &= \left( 2 - \frac{c + \left\lfloor\frac{m}{2}\right\rfloor}{2^{23}} \right)\cdot2^{(-e+125)/2} \\ \end{align*}
となる。真の\(\frac{1}{\sqrt{y}}\)との比を取ると、
\begin{align*} g(y)\sqrt{y} &= \frac{1}{2}\left( 2 - \frac{c + \left\lfloor\frac{m}{2}\right\rfloor}{2^{23}} \right)\sqrt{1 + \frac{m}{2^{23}}} \end{align*}
となり、\(e\)によらず\(m\)のみで表せることがわかる。
\(e\)が偶数のとき
\(e\)が偶数\(e=2n\)のとき、
\begin{align*} g(y) &= f^{-1}\left((381 - e)\cdot2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ &= f^{-1}\left(\left(381 - 2n\right)\cdot2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ &= f^{-1}\left(\left(190 - n\right)\cdot2^{23} + 2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ \end{align*}
ここで、\(2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\)が負の場合と非負の場合で分岐する。
\begin{align*} & 2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right) \geq 0 \\ \Leftrightarrow \:& 2^{22} - c \geq \left\lfloor\frac{m}{2}\right\rfloor \\ \Leftrightarrow \:& 2^{22} - (c - 1)\geq \frac{m}{2} \\ \Leftrightarrow \:& 2^{23} - 2(c - 1)\geq m \\ \end{align*}
なので、\(m\leq2^{23} - 2(c - 1)\)の場合と\(2^{23} - 2(c - 1)<m\)の場合で場合分けする。
\(m\leq2^{23} - 2(c - 1)\)のとき、
\begin{align*} g(y) &= f^{-1}\left(\left(190 - n\right)\cdot2^{23} + 2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ &= \left(1+\frac{2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)}{2^{23}}\right)\cdot2^{190 - n - 127} \\ &= \left(\frac{3}{2} - \frac{c + \left\lfloor\frac{m}{2}\right\rfloor}{2^{23}}\right)\cdot2^{(-e+126)/2} \\ \end{align*}
となり、真の\(\frac{1}{\sqrt{y}}\)との比は、
\begin{align*} g(y)\sqrt{y} &= \frac{1}{\sqrt{2}}\left( \frac{3}{2} - \frac{c + \left\lfloor\frac{m}{2}\right\rfloor}{2^{23}} \right)\sqrt{1 + \frac{m}{2^{23}}} \end{align*}
となる。
\(2^{23} - 2(c - 1) < m\)のとき、
\begin{align*} g(y) &= f^{-1}\left(\left(190 - n\right)\cdot2^{23} + 2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ &= f^{-1}\left(\left(189 - n\right)\cdot2^{23} + 2^{23} + 2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)\right) \\ &= \left(1 + \frac{2^{23} + 2^{22} - \left(c + \left\lfloor\frac{m}{2}\right\rfloor\right)}{2^{23}}\right)\cdot2^{189 - n - 127} \\ &= \left(\frac{5}{2} - \frac{c + \left\lfloor\frac{m}{2}\right\rfloor}{2^{23}}\right)\cdot2^{(-e+124)/2} \\ \end{align*}
となり、真の\(\frac{1}{\sqrt{y}}\)との比は、
\begin{align*} g(y)\sqrt{y} &= \frac{1}{2^{3/2}}\left( \frac{5}{2} - \frac{c + \left\lfloor\frac{m}{2}\right\rfloor}{2^{23}} \right)\sqrt{1 + \frac{m}{2^{23}}} \end{align*}
となる。
具体例
\(c=0\)の場合(無補正)と\(c=566817\)の場合(Quake III Arenaの実装)を比べると、\(g(y)\sqrt{y}\)の比は次の図のようになる。
定数に補正を加えることによって、\(e\)が奇数の場合も偶数の場合も真の逆平方根との比は96%~104%の間に収まっていることがわかる。
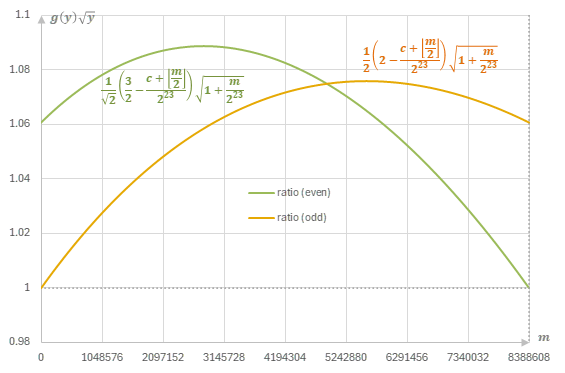
type punningによる近似と真の逆平方根の比 (c=0)
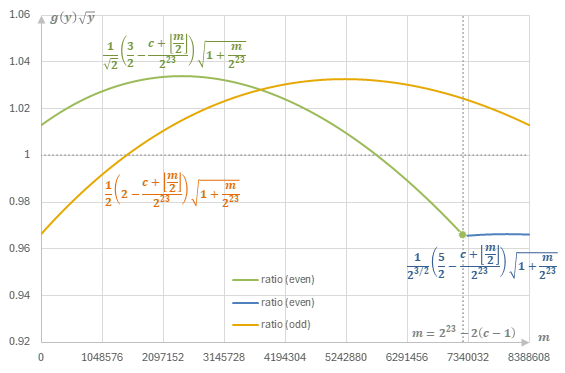
type punningによる近似と真の逆平方根の比 (c=566817)
Quake III Arenaの実装では、逆平方根の近似値は次のグラフのようになる。
type punningだけではまだグラフは歪な形だが、Newton法を1回適用するだけで真の逆平方根とほぼ一致する。
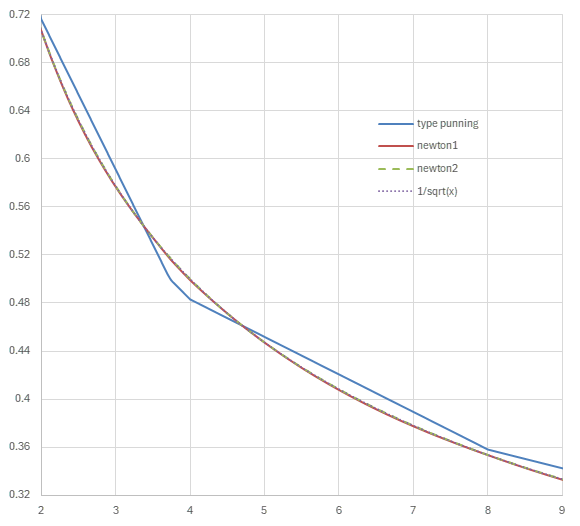
各段階における逆平方根の近似 (c=566817)
例えば\(y=60296272\)というfloat型の値(\(e=152, m=6685460\))は、
| 段階 | 値 | 比 |
|---|---|---|
| type punning | 0.00012621407222468 | 0.98006077 |
| Newton法1回 | 0.00012870559277151 | 0.99940760 |
| Newton法2回 | 0.00012878181475133 | 0.99999947 |
| 真の\(\frac{1}{\sqrt{y}}\) | 0.00012878188252846 | 1.00000000 |
というように近似される。この計算例からも、type punningとNewton法の適用によって十分な精度の近似値が得られることがわかる。
参考
- Quake-III-Arena/code/game/q_math.c at master · id-Software/Quake-III-Arena · GitHub
- The Fast Inverse Square Root
- 1/√xを計算する変態コード【ゆっくり解説】 - YouTube
- 高速逆平方根(fast inverse square root)のアルゴリズム解説 - 滴了庵日録
- 0x5f3759df | Hummus and Magnets
- Chris Lomont - Fast Inverse Square Root
- [1603.04483] Fast calculation of inverse square root with the use of magic constant \(-\) analytical approach
- Fast inverse square root - Wikipedia