3D Gaussian Splatting

概要

NVS (Novel View Synthesis) は、既存の複数の画像から新しい視点の画像を生成する技術分野。LiDARなどの特別な機器を用いず、一般的なカメラで撮影した画像だけで3次元空間を再構成することを目的とした比較的新しい分野で、3次元データを扱う様々な領域への活用が期待されている。
NVSを用いれば、実世界の物体を様々な方向から撮影した画像データセットから学習して、撮影されていない全く別の方向からの画像を予測して生成することが可能となる。

NVSの例 (NeRFの論文から引用)

NVSの実装の一つとして2020年にNeRF(Neural Radiance Fields)が登場した。
NeRFでは、「3次元空間の各座標」 (3次元) と「その座標に対するカメラの方向を表す立体角」 (2次元) の5次元値を引数に取り、「カメラに届く光の放射輝度」を出力する放射輝度場 (Radiance Field) を考える。そのような放射輝度場をニューラルネットワークで表現することで新視点画像の生成を可能にし、実際に撮影された画像との差異を減らすように学習が実行される。
この手法は従来に比べて非常に品質が高いことから注目を集めたが、高画質を求めるほど1枚の2次元画像を生成するために (x, y, z) の3パラメーターに対して細かく反復計算を行う必要があり、結果として生成時間が長くなるという欠点が指摘されていた。

3DGS (3D Gaussian Splatting) は2023年に発表されたNVSの実装の一種。
3DGSでは、新視点画像の生成に必要な情報を3次元空間上の点群に付与し、各点からの色の広がりの情報を学習することによって新視点画像の生成を可能にしている。点群を用いることによって、「何もない空間」での計算を省略することができ、また逆に情報の多い領域には点群をより集中させることができるので、NeRFに比べて軽量でありながら高画質化が達成された。
3DGSは勾配降下法によって学習を行うが、ニューラルネットワークを用いないことも大きな特徴である。

この投稿では3DGSの仕組みを解説する。

パラメーター構造

3DGSは3次元空間上の点群を基にし、それらを同一空間内のカメラへ投影することで画像を生成する。
ただし、3DGSで扱う点群は単なる3次元の位置ベクトルではなく、投影に用いる諸情報を付与することで拡張された自由度58のベクトルである。この自由度58のベクトルをGaussianと呼ぶ。
Gaussianの各成分は次の内容で構成される。位置と基本色は後述のSfMの出力で初期化される。

3次元空間上の位置\(P\) (自由度3)
共分散行列\(\Sigma\) (自由度6)
球面調和関数のパラメーター\(c_{l,m}\) (自由度48)
- 3DGSでは\(l=3\)までを扱い、それが3色分で\(3\times(1+3+5+7)=48\)パラメーターになる
- そのうち\(l=0\)に相当する3パラメーターは基本色に該当
透明度\(\alpha\) (自由度1)

分散共分散行列

3DGSでは、3次元空間上の点群は色の広がりの情報を持つものと考える。
色の広がりは点の位置\(P\)を中心とした3次元Gauss関数 (=正規分布) で表される。つまり、各Gaussianは中心座標\(P\)に加えて共分散行列\(\Sigma\)を調整可能なパラメーターとして持ち、3次元空間上の点\(r\)においては

\begin{align*} p_{r}(r|P,\Sigma) &= p_\mathcal{N}(r|P,\Sigma) \\ &\propto \exp\left(-\frac{1}{2} (r-P)^\top\Sigma^{-1}(r-P) \right) \end{align*}

に従って中心座標\(P\)からの色の広がりの影響を受けることになる。(係数は透明度パラメーター\(\alpha\)に吸収されるので省略できる)

3次元空間における正規分布による色の広がり

ここで、共分散行列は3x3の正定値行列でなければならず、3x3行列の9つのパラメーター全てが自由な値を取れるわけではない。
正定値行列に対しては回転・伸縮による分解\(\Sigma=QSSQ^\top\)や、Cholesky分解\(\Sigma=LL^\top\)ができることから、正定値行列の実際の自由度は6である。
3DGSの公式実装では回転・伸縮による分解を採用し、回転行列\(Q\)は更に四元数\(q=(q_r, q_x, q_y, q_z)\)による分解を用いて表現している。(ただし\(q_r^2+q_x^2+q_y^2+q_z^2=1\))

\begin{align*} Q = \begin{pmatrix} 1-2(q_y^2+q_z^2) & 2(q_xq_y-q_rq_z) & 2(q_xq_z+q_yq_r) \\ 2(q_xq_y+q_zq_r) & 1-2(q_x^2+q_z^2) & 2(q_yq_z-q_rq_x) \\ 2(q_xq_z-q_rq_y) & 2(q_yq_z+q_rq_x) & 1-2(q_x^2+q_y^2) \end{pmatrix} \end{align*}

なお、\(\Sigma=QSSQ^\top\)あるいは\(\Sigma=LL^\top\)という分解の表現は、パラメーターを自由に変化させると\(\Sigma\)が半正定値行列にもなり得るので、実装では確実に正定値行列にするために対角成分に微小な定数を加えることがある。

\begin{align*} \Sigma \leftarrow \Sigma + \varepsilon I \end{align*}

球面調和関数の係数

3DGSでは球面調和関数を用いることで、見る方向によるGaussianの色の変化を学習するよう設計されている。
球面調和関数\(\{Y_{l,m}(\theta,\phi)\}_{l,m}\)は3次元空間上の単位球面\(S^2\)上で定義される関数の集合であり、その線形結合によって\(L^2\left(S^2\right)\)の関数を任意の精度で近似できるという性質がある。球面上の値を中心からその方向に放射される光の強さと捉えれば、球面調和関数を用いて見る方向による色の変化を表現することができるようになる。

球面調和関数によって球面上の色を近似する例

球面調和関数では具体的には、

\begin{align*} R(\theta,\phi) = \sum_{l=L}^L \sum_{m=-l}^l c_{l,m}^{(R)}Y_{l,m}(\theta.\phi) \end{align*}

とすることで、見る方向\(\theta, \phi\)に依存した色\(R\)を\(\{c_{l,m}^{(R)}\}_{l,m}\)によってパラメーター化する。これはB, Gについても同様。
(具体的な関数\(Y_{l,m}(\theta,\phi)\)についてはこちらに掲載)

\(L=\infty\)ならば\(R(\theta,\phi)\)を正確に再現することができるが、コンピューター上の計算では無限のパラメーターを取ることはできないので、有限で打ち切ることで近似している。
3DGSの公式実装では\(L=3\)までを扱い、R･G･Bそれぞれに16パラメーター (=1+3+5+7) が割り当てられることになる。(つまり合計48パラメーター (=3×16) になる)

なお、\(Y_{0,0}(\theta,\phi)=\frac{1}{2\sqrt{\pi}}\)は球面全体で同じ値を取る定数関数であり、対応する係数\(c_{0,0}\)は球面上の平均値を表す。したがって後述の初期化の処理では、SfMで算出された各点の基本色を\(2\sqrt{\pi}\)倍して\(c_{0,0}\)に代入する。

球面調和関数パラメーターの数を変化させたときの3DGSの学習結果の比較。
左から (球面調和関数パラメーターが) 3個の場合、48個の場合、実際に撮影された写真。
結果にほとんど差は感じられないが、球面調和関数パラメーターが3個の場合は48個の場合に比べて学習が1.4倍ほど早い。

レンダリング (推論)

Gaussianのパラメーターが最適化済み (=学習済み) であると想定し、指定されたカメラパラメーター\((R, t, K)\)に対してGaussianから画像をレンダリング (平面射影) する流れを追う。

点群の平面射影

カメラの姿勢が回転行列\(R\in SO(3)\)と平行移動\(t\in\mathbb{R}\)で特徴付けられるとき、点群に含まれる点\(P\)はカメラ座標系Cでは

\begin{align*} P_C = R^\top(P - t) \end{align*}

という座標で表される。(カメラ座標系Cに対して、変換前の\(P\)が属する座標系を世界座標系Wと呼ぶ)

透視投影

更に、カメラ座標系Cで表される\(P_C\)を透視投影することで、2次元の画像座標系Iにおける座標\(p=(x,y)\)が得られる。

\begin{align*} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} &= K \begin{pmatrix} X_C/Z_C \\ Y_C/Z_C \\ 1 \end{pmatrix} \\ &= \begin{pmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} X_C/Z_C \\ Y_C/Z_C \\ 1 \end{pmatrix} \\ &= \begin{pmatrix} f_x\frac{X_C}{Z_C} + c_x \\ f_y\frac{Y_C}{Z_C}+c_y \\ 1 \end{pmatrix} \\ \end{align*}

座標系Cから座標系Iへの変換を\(p=u(P_C)\)と表すことにする。

\begin{align*} u(P_C) &= \begin{pmatrix} x \\ y \end{pmatrix} \\ &= \begin{pmatrix} f_x\frac{X_C}{Z_C} + c_x \\ f_y\frac{Y_C}{Z_C}+c_y \end{pmatrix} \\ \end{align*}

共分散行列の平面射影

共分散行列は座標系Wにおいて

\begin{align*} \Sigma = \mathbb{E}_r\left((r-P)(r-P)^\top\right) \end{align*}

と定義される。

このとき、座標系Cに変換した分布も正規分布になり、

\begin{align*} \Sigma_C &= \mathbb{E}_{r_C}\left((r_C-P_C)(r_C-P_C)^\top\right) \\ &= \mathbb{E}_r\left((R^\top(r-t)-R^\top(P-t))(R^\top(r-t)-R^\top(P-t))^\top\right) \\ &= \mathbb{E}_r\left(R^\top(r-P)(r-P)^\top R\right) \\ &= R^\top\mathbb{E}_r\left((r-P)(r-P)^\top\right)R \\ &= R^\top\Sigma R \\ \end{align*}

となる。

また、\(\delta:=r_C-P_C\)が微少量であると見なすと、

\begin{align*} r_I &= u(r_C) \\ &= u(P_C+\delta) \\ &= u(P_C) + \frac{\partial u}{\partial r_C}(P_C)\cdot \delta + O(\|\delta\|^2) \\ &= p + J\delta + O(\|\delta\|^2) \\ \end{align*}

と近似できる。ただし、

\begin{align*} J &:= \frac{\partial u}{\partial r_C}(P_C) \\ &= \begin{pmatrix} \frac{\partial u_x}{\partial X_C}(P_C) & \frac{\partial u_x}{\partial Y_C}(P_C) & \frac{\partial u_x}{\partial Z_C}(P_C) \\ \frac{\partial u_y}{\partial X_C}(P_C) & \frac{\partial u_y}{\partial Y_C}(P_C) & \frac{\partial u_y}{\partial Z_C}(P_C) \\ \end{pmatrix} \\ &= \begin{pmatrix} \frac{f_x}{Z_C} & 0 & -\frac{f_xX_C}{Z_C^2} \\ 0 & \frac{f_y}{Z_C} & -\frac{f_yY_C}{Z_C^2} \\ \end{pmatrix} \\ \end{align*}

はJacobi行列と呼ばれる行列である。
したがって、座標系Iにおける平均は

\begin{align*} \mu_I &= \mathbb{E}_{r_I}(r_I) \\ &= \mathbb{E}_{r_C}(p + J\delta + O(\|\delta\|^2)) \\ &= p + J\mathbb{E}_{r_C}(\delta) + O(\|\delta\|^2) \\ &= p + J\cdot 0 + O(\|\delta\|^2) \\ &= p + O(\|\delta\|^2) \\ \end{align*}

となり、共分散行列は、

\begin{align*} \Sigma_I &= \mathbb{E}_{r_I}\left((r_I-\mu_I)(r_I-\mu_I)^\top\right) \\ &= \mathbb{E}_{r_I}\left((r_I-p + O(\|\delta\|^2))(r_I-p + O(\|\delta\|^2))^\top\right) \\ &= \mathbb{E}_{r_C}\left(\left(J\delta + O(\|\delta\|^2)\right)\left(J\delta + O(\|\delta\|^2)\right)^\top\right) \\ &= \mathbb{E}_{r_C}\left(J\delta\delta^\top J^\top\right) + O(\|\delta\|^3) \\ &= J\mathbb{E}_{r_C}\left((r_C-P_C)(r_C-P_C)^\top\right)J^\top + O(\|\delta\|^3) \\ &= J\Sigma_CJ^\top + O(\|\delta\|^3) \\ &= JR^\top\Sigma RJ^\top + O(\|\delta\|^3) \\ \end{align*}

と近似できる。

正規分布を透視投影で2次元に投影した分布は複雑になり、高速に大量の点を扱う3DGSで正確な分布を表現することは現実的ではないので、2次元でも正規分布に従うものとして近似することにする。また、その共分散行列は\(\Sigma_I=JR\Sigma R^\top J^\top\)と近似する。

\begin{align*} p_{r_I}(r_I|p,\Sigma_I) &\approx p_\mathcal{N}\left(r_I\middle|p,JR\Sigma R^\top J^\top\right) \\ &\propto \exp\left(-\frac{1}{2}(r_I-p)^\top\left(JR^\top\Sigma RJ^\top\right)^{-1}(r_I-p)\right) \end{align*}

3次元正規分布を正確に透視投影した分布の等高線 (赤) と、近似された正規分布の等高線 (緑) の例。dFOV=200°

3DGSではこの先2次元の共分散行列\(\Sigma_I\)の逆行列\(\Sigma_I^{-1}\)を求める必要があるが、前述の通り\(\Sigma\)は半正定値 (非正則) になり得るので、実装では対角成分に定数を加えることで正定値性を保証している。公式実装では\(\varepsilon=0.3\)が用いられる。

\begin{align*} \Sigma_I \leftarrow \Sigma_I + \varepsilon I \end{align*}

球面調和関数による色の決定

3DGSでは座標系Wにおける球面調和関数によって、見る方向による色の変化を表現している。したがって、射影される色を求めるには、座標系WにおけるカメラとGaussianの位置の関係から「見る方向」を計算する必要がある。
3DGSの実装では、座標系Wにおけるカメラの座標を\(C_W\)としたとき、「座標系Wにおいて位置\(P\)に存在するGaussianを見る方向」を

\begin{align*} d := P - C_W \end{align*}

と定めている。

Gaussian (橙色の点) を見る方向。青はW座標系で、赤はC座標系を表す。

ここで、\(C_W\)はカメラ座標系における原点なので、

\begin{align*} 0 = R^\top(C_W - t) \end{align*}

つまり

\begin{align*} C_W = t \end{align*}

が成り立つ。
したがって、「座標系WにおいてGaussianを見る方向」は

\begin{align*} d &= P - C_W \\ &= P - t \\ &= RP_C \\ \end{align*}

と表すことができる。(\(R^{-1}=R^\top\))

球面調和関数\(Y_{l,m}(\theta,\phi)\)には単位球面上における直交座標表示\(Y_{l,m}(x,y,z)\)が存在するので、\((x,y,z)=\frac{d}{\|d\|}\)とすれば角度への変換を要さずにそれぞれの球面調和関数の値を求めることができる。
最終的に投影に反映される色は、Gaussianが持つ球面調和関数パラメーターを\(c_{l,m}^{(R)}\)とすると、

\begin{align*} R = \sum_{l=0}^L \sum_{m=-l}^l c_{l,m}^{(R)}Y_{l,m}(x,y,z) \end{align*}

と計算することができる。(B, Gも同様)

アルファブレンド

Gaussianの総数を\(N\)とすると、これまでの過程によって次の情報が利用可能な状態になっている。

不透明度\(\{\alpha^{(n)}\}_{n=1}^N\): Gaussianのパラメーターに直接含まれる
投影された中心座標\(\{p^{(n)}\}_{n=1}^N\): 「点群の平面射影」で計算済み
(近似的に) 投影された共分散行列\(\{\Sigma_I^{(n)}\}_{n=1}^N\): 「共分散行列の平面射影」で計算済み
色\(\{c^{(n)}\}_{n=1}^N\): 「球面調和関数による色の決定」で計算済み

Gaussianが共分散行列によって平面的な広がりを持つということは、1つのGaussianにつき共分散行列から不透明度が計算された1枚のレイヤーが存在し、Gaussianと同じ数のレイヤーが重なっていることと同じことである。
3DGSの最終的な出力画像を得るには、ここまでの過程で得た情報からGaussianごとにレイヤーを作り、レイヤーをアルファブレンドして1枚のレイヤーにまとめる必要がある。

アルファブレンドはレイヤーの前後によって結果が変わるので、カメラから見た前後関係によってGaussianを並べ替えなければならない。つまり、カメラ座標へ変換された\(Z_C\)が正のGaussianのみを抽出し、\(Z_C\)について昇順で並べ替えなければならない。
この処理は3DGSの公式実装ではCUDA言語を用いた基数ソートで実装されている。(並列化しやすいことと、比較処理が不要であることから、基数ソートはGPUと相性が良い)

Gaussianの前後関係

ソート後に書くGaussianからレイヤーを作る。
レイヤー\(n\)の位置\(i,j\)の不透明度\(A^{(n)}_{ij}\)と色\(C^{(n)}_{ij}\)は次のように決められる。

\begin{align*} \left\{ \begin{array}{ll} A^{(n)}_{ij} = \alpha^{(n)}\exp\left(-\frac{1}{2}\left(r_{ij}-p^{(n)}\right)^\top{\Sigma_I^{(n)}}^{-1}\left(r_{ij}-p^{(n)}\right)\right) \\ C^{(n)}_{ij} = c^{(n)} \\ \end{array} \right. \end{align*}

なお、\(r_{ij}=\begin{pmatrix}j\\i\end{pmatrix}\)である。また、\(C\)はRGBの3つの成分を持つ。

Gaussianのレイヤー合成処理

アルファブレンド

一般に、色と不透明度が\(\left(C^{(1)},A^{(1)}\right),\left(C^{(2)},A^{(2)}\right)\)の2つのレイヤーが重なっているとする。(各\(C\)はRGBの成分を持つ)
レイヤー1が手前でレイヤー2が奥の場合、2枚のレイヤーは合成して新たな1枚のレイヤーと見なすことができ、その色と不透明度\((C,A)\)はピクセルごとに、

\begin{align*} A &= A^{(1)} + \left(1-A^{(1)}\right)A^{(2)} \\ &= 1 - \left(1-A^{(1)}\right)\left(1-A^{(2)}\right) \\ C &= \frac{A^{(1)}C^{(1)} + \left(1-A^{(1)}\right)A^{(2)}C^{(2)}}{A} \end{align*}

と表すことができる。

手前から\(n\)枚のレイヤー\(\left(C^{(1)},A^{(1)}\right),\cdots,\left(C^{(n)},A^{(n)}\right)\)を合成したレイヤーの色と不透明度を\(\left(C^{(:n)},A^{(:n)}\right)\)と表す。
このとき、\(n-1\)枚のレイヤーを合成した\(\left(C^{(:n-1)},A^{(:n-1)}\right)\)を手前のレイヤー、\(n\)枚目のレイヤー\((C^{(n)},A^{(n)})\)を奥のレイヤーと見なすことができる。

したがって、\(n\)枚まで合成したときの不透明度は、

\begin{align*} 1 - A^{(:n)} &= \left(1-A^{(:n-1)}\right)\left(1-A^{(n)}\right) \\ &= \left(1-A^{(:n-2)}\right)\left(1-A^{(n-1)}\right)\left(1-A^{(n)}\right) \\ &\;\;\vdots \\ &= \left(1-A^{(:1)}\right)\left(1-A^{(2)}\right)\cdots\left(1-A^{(n-1)}\right)\left(1-A^{(n)}\right) \\ &= \left(1-A^{(1)}\right)\left(1-A^{(2)}\right)\cdots\left(1-A^{(n-1)}\right)\left(1-A^{(n)}\right) \\ &= \prod_{m=1}^n \left(1-A^{(m)}\right) \\ \end{align*}

となることから

\begin{align*} A^{(:n)} &= 1 - \prod_{m=1}^n \left(1-A^{(m)}\right) \\ \end{align*}

となる。ここで便宜上、\(A^{(:0)}\)を

\begin{align*} A^{(:0)} &:= 1 - \prod_{m=1}^0 \left(1-A^{(m)}\right) \\ &= 1 - 1 \\ &= 0 \end{align*}

と表すことにする。

また、\(n\)枚まで合成したときの色は、

\begin{align*} A^{(:n)}C^{(:n)} &= A^{(:n-1)}C^{(:n-1)} + \left(1-A^{(:n-1)}\right)A^{(n)}C^{(n)} \\ &= A^{(:n-2)}C^{(:n-2)} + \left(1-A^{(:n-2)}\right)A^{(n-1)}C^{(n-1)} + \left(1-A^{(:n-1)}\right)A^{(n)}C^{(n)} \\ &\;\;\vdots \\ &= A^{(:1)}C^{(:1)} + \left(1-A^{(:1)}\right)A^{(2)}C^{(2)} + \cdots + \left(1-A^{(:n-2)}\right)A^{(n-1)}C^{(n-1)} + \left(1-A^{(:n-1)}\right)A^{(n)}C^{(n)} \\ &= \left(1-A^{(:0)}\right)A^{(1)}C^{(1)} + \left(1-A^{(:1)}\right)A^{(2)}C^{(2)} + \cdots + \left(1-A^{(:n-2)}\right)A^{(n-1)}C^{(n-1)} + \left(1-A^{(:n-1)}\right)A^{(n)}C^{(n)} \\ &= \sum_{m=1}^n \left(1-A^{(:m-1)}\right)A^{(m)}C^{(m)} \\ \end{align*}

となることから、

\begin{align*} C^{(:n)} &= \frac{\sum_{m=1}^n \left(1-A^{(:m-1)}\right)A^{(m)}C^{(m)}}{A^{(:n)}} \\ \end{align*}

となる。
この計算を繰り返し適用することで、最終的な出力画像にあたる\(\bar{C}:=C^{(:N)},\bar{A}:=A^{(:N)}\)を得ることができる。

なお、

\begin{align*} \left\{ \begin{array}{ll} T^{(:n)} = 1-A^{(:n)} \\ P^{(:n)} = A^{(:n)}C^{(:n)} \\ \end{array} \right. \end{align*}

とすることで、漸化式を

\begin{align*} T^{(:n)} &= T^{(:n-1)}\left(1-A^{(n)}\right) \\ \end{align*}

\begin{align*} P^{(:n)} &= P^{(:n-1)} + T^{(:n-1)}A^{(n)}C^{(n)} \\ \end{align*}

と簡潔に表すこともできる。
不透明度 (opacity) \(\alpha\)に対して\(T=1-\alpha\)をtransmittanceと言い、\(P=AC\)をpremultiplied alphaと言う。
アルファブレンド時の背景色を\(C_{bg}\)とすると、最終的な出力画像の各ピクセルのRGB値は\(\bar{P} + \bar{T}C_{bg}\)となるが、3DGS公式実装では\(C_{bg}=0\)なので出力画像は\(\bar{P}\)そのものであり、\(\bar{T}\)は損失関数は直接寄与しないことになる。

3DGSの実装では描画範囲を考慮したアルファブレンドを行っている。
\(\lambda_\text{max}\)を2次元投影された共分散行列\(\Sigma_I\)の最大固有値とすると、2次元位置座標\(p\)を中心とする半径\(3\sqrt{\lambda_\text{max}}\)の円の内側をそのGaussianの描画範囲とし、その内側の値だけをアルファブレンドによって合成する。
円が投影画像の領域と共通部分を持たないとき、そのGaussianのアルファブレンドはスキップされる。
Gaussianが描画されたかどうかの結果は、学習時のGaussianの複製・分割の判定の際に利用される。

逆伝播の実装

前述のような大量のGaussianをレイヤーに変換して合成していく繰り返し処理は、計算グラフを複雑にし学習時の消費VRAMを大幅に引き上げてしまうという問題がある。この問題はGaussianの総数が多いほど深刻になり、通常何百万個もの点群を扱う3DGSでは普通に実装しただけでは現実的な環境で学習を動作させることは不可能である。
そこで、レイヤー合成の処理をautograd.Functionで自前実装し、レイヤー合成処理全体の逆伝播 (backward) を手計算で求めた導関数によって1つの関数に整理して実装し直すことで、VRAM消費の軽減を試みる。

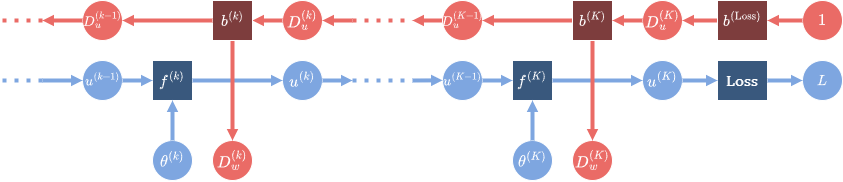
最終的な損失関数が\(L\)であるニューラルネットワークについて、ある層の順伝播(forward) の入力が\(x\)、出力が\(y\)であるとする。
誤差逆伝播法ではこのとき、逆伝播(backward) の際に計算グラフの出力側 (下図の右側) から来た\(D_y := \frac{\partial L}{\partial y}\)に対して、\(D_x := \frac{\partial L}{\partial x}\)を計算グラフの入力側 (下図の左側) に伝えなければならない。

これは微分の連鎖率を用いることによって、

\begin{align*} \frac{\partial L}{\partial x} &= \frac{\partial L}{\partial y}\frac{\partial y}{\partial x} \\ \end{align*}

と表すことができるので、各層のbackwardでは\(\frac{\partial y}{\partial x}\)を実装さえすれば、入力\(\frac{\partial L}{\partial y}\)から出力\(\frac{\partial L}{\partial x}\)を求めることができるようになる。
(\(\frac{\partial L}{\partial x}, \frac{\partial L}{\partial y}\)は\(x^\top,y^\top\)と大きさの行ベクトルで、\(\frac{\partial y}{\partial x}\)は\(yx^\top\)と同じ大きさの行列)

自動微分の仕組み (青がforward、赤がbackwardを表す)

forwardの入力は\(\alpha, p, \Sigma_I^{-1}, c\)で、出力は\(\bar{T}, \bar{P}\)である。(ここでは実際の実装に基づいて\(\bar{A},\bar{C}\)ではなく\(\bar{T}, \bar{P}\)を用いることにする)
このときbackwardは、入力\(\frac{\partial L}{\partial \bar{T}}, \frac{\partial L}{\partial \bar{P}}\)を用いて\(\frac{\partial L}{\partial \alpha}, \frac{\partial L}{\partial p}, \frac{\partial L}{\partial \Sigma_I^{-1}}, \frac{\partial L}{\partial c}\)を計算して返さなくてはならない。その値はそれぞれ、

\begin{align*} \frac{\partial L}{\partial \alpha^{(n)}} &= \sum_{ij} \frac{\partial L}{\partial A^{(n)}_{ij}}\frac{\partial A^{(n)}_{ij}}{\partial \alpha^{(n)}} \\ &= \sum_{ij} \left( \frac{\partial L}{\partial \bar{T}_{ij}}\frac{\partial \bar{T}_{ij}}{\partial A^{(n)}_{ij}} + \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial A^{(n)}_{ij}} \right) \frac{\partial A^{(n)}_{ij}}{\partial \alpha^{(n)}} \\ \end{align*}

\begin{align*} \frac{\partial L}{\partial p^{(n)}} &= \sum_{ij} \frac{\partial L}{\partial A^{(n)}_{ij}}\frac{\partial A^{(n)}_{ij}}{\partial p^{(n)}} \\ &= \sum_{ij} \left( \frac{\partial L}{\partial \bar{T}_{ij}}\frac{\partial \bar{T}_{ij}}{\partial A^{(n)}_{ij}} + \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial A^{(n)}_{ij}} \right) \frac{\partial A^{(n)}_{ij}}{\partial p^{(n)}} \\ \end{align*}

\begin{align*} \frac{\partial L}{\partial {\Sigma_I^{(n)}}^{-1}} &= \sum_{ij} \frac{\partial L}{\partial A^{(n)}_{ij}}\frac{\partial A^{(n)}_{ij}}{\partial {\Sigma_I^{(n)}}^{-1}} \\ &= \sum_{ij} \left( \frac{\partial L}{\partial \bar{T}_{ij}}\frac{\partial \bar{T}_{ij}}{\partial A^{(n)}_{ij}} + \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial A^{(n)}_{ij}} \right) \frac{\partial A^{(n)}_{ij}}{\partial {\Sigma_I^{(n)}}^{-1}} \\ \end{align*}

\begin{align*} \frac{\partial L}{\partial c^{(n)}} &= \sum_{ij} \frac{\partial L}{\partial C^{(n)}_{ij}}\frac{\partial C^{(n)}_{ij}}{\partial c^{(n)}} \\ &= \sum_{ij} \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial C^{(n)}_{ij}} \frac{\partial C^{(n)}_{ij}}{\partial c^{(n)}} \\ &= \sum_{ij} \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial C^{(n)}_{ij}} \\ \end{align*}

と表される。(\(\frac{\partial L}{\partial p^{(n)}}\)は\({p^{(n)}}^\top\)と同じ大きさの行ベクトルで、\(\frac{\partial L}{\partial \Sigma^{(n)}}\)は\(\Sigma^{(n)}\)と同じ大きさの行列)
背景色が黒の場合は\(\frac{\partial L}{\partial \bar{T}_{ij}}=0\)なので項を減らすことができるが、ここでは背景が黒以外で学習する場合も考慮することにする。

各部分は更に、

\begin{align*} \frac{\partial \bar{T}_{ij}}{\partial A^{(n)}_{ij}} &= \frac{\partial}{\partial A^{(n)}_{ij}}\left(1-A^{(:N)}_{ij}\right) \\ &= \frac{\partial}{\partial A^{(n)}_{ij}}\prod_{m=1}^N\left(1-A^{(m)}_{ij}\right) \\ &= \frac{\partial \left(1-A^{(n)}_{ij}\right)}{\partial A^{(n)}_{ij}}\prod_{\substack{m=1\\m\neq n}}^N\left(1-A^{(m)}_{ij}\right) \\ &= -\prod_{\substack{m=1\\m\neq n}}^N\left(1-A^{(m)}_{ij}\right) \\ &= -\frac{\bar{T}_{ij}}{1-A^{(n)}_{ij}} \end{align*}

\begin{align*} \frac{\partial \bar{P}_{ij}}{\partial A^{(n)}_{ij}} &= \frac{\partial}{\partial A^{(n)}_{ij}}\left( \sum_{m=1}^N T^{(:m-1)}_{ij}A^{(m)}_{ij}C^{(m)}_{ij} \right) \\ &= \left( \sum_{m=n+1}^N \frac{\partial T^{(:m-1)}_{ij}}{\partial A^{(n)}_{ij}}A^{(m)}_{ij}C^{(m)}_{ij} + T^{(:n-1)}_{ij}C^{(n)}_{ij} \right) \\ &= \left( - \sum_{m=n+1}^N \frac{T^{(:m-1)}_{ij}}{1-A^{(n)}_{ij}}A^{(m)}_{ij}C^{(m)}_{ij} + T^{(:n-1)}_{ij}C^{(n)}_{ij} \right) \\ &= \frac{1}{1-A^{(n)}_{ij}} \left( - \sum_{m=n+1}^N T^{(:m-1)}_{ij}A^{(m)}_{ij}C^{(m)}_{ij} + T^{(:n)}_{ij}C^{(n)}_{ij} \right) \\ &= \frac{1}{1-A^{(n)}_{ij}} \left( P^{(:n)}_{ij} - \bar{P}_{ij} + T^{(:n)}_{ij}C^{(n)}_{ij} \right) \\ \end{align*}

\begin{align*} \frac{\partial \bar{P}_{ij}}{\partial C^{(n)}_{ij}} &= \frac{\partial}{\partial C^{(n)}_{ij}}\left( \sum_{m=1}^N T^{(:m-1)}_{ij}A^{(m)}_{ij}C^{(m)}_{ij} \right) \\ &= T^{(:n-1)}_{ij}A^{(n)}_{ij} \\ \end{align*}

\begin{align*} \frac{\partial A^{(n)}_{ij}}{\partial \alpha^{(n)}} &= \frac{\partial}{\partial \alpha^{(n)}}\left(\alpha^{(n)}\exp\left(-\frac{1}{2}\left(r_{ij}-p^{(n)}\right)^\top{\Sigma_I^{(n)}}^{-1}\left(r_{ij}-p^{(n)}\right)\right)\right) \\ &= \exp\left(-\frac{1}{2}\left(r_{ij}-p^{(n)}\right)^\top{\Sigma_I^{(n)}}^{-1}\left(r_{ij}-p^{(n)}\right)\right) \\ &= \frac{A^{(n)}_{ij}}{\alpha^{(n)}} \\ \end{align*}

\begin{align*} \frac{\partial A^{(n)}_{ij}}{\partial p^{(n)}} &= \frac{\partial}{\partial p^{(n)}}\left(\alpha^{(n)}\exp\left(-\frac{1}{2}\left(r_{ij}-p^{(n)}\right)^\top{\Sigma_I^{(n)}}^{-1}\left(r_{ij}-p^{(n)}\right)\right)\right) \\ &= A^{(n)}_{ij} \frac{\partial}{\partial p^{(n)}}\left(-\frac{1}{2}\left(r_{ij}-p^{(n)}\right)^\top{\Sigma_I^{(n)}}^{-1}\left(r_{ij}-p^{(n)}\right)\right) \\ &= A^{(n)}_{ij} \left(-\frac{1}{2}\cdot2\left(p^{(n)}-r_{ij}\right)^\top{\Sigma_I^{(n)}}^{-1}\right) \\ &= A^{(n)}_{ij} \left(r_{ij} - p^{(n)}\right)^\top{\Sigma_I^{(n)}}^{-1} \\ &= A^{(n)}_{ij} \left( {\Sigma_I^{(n)}}^{-1}\left(r_{ij} - p^{(n)}\right) \right)^\top \\ \end{align*}

\begin{align*} \frac{\partial A^{(n)}_{ij}}{\partial {\Sigma_I^{(n)}}^{-1}} &= \frac{\partial}{\partial {\Sigma_I^{(n)}}^{-1}}\left(\alpha^{(n)}\exp\left(-\frac{1}{2}\left(r_{ij}-p^{(n)}\right)^\top{\Sigma_I^{(n)}}^{-1}\left(r_{ij}-p^{(n)}\right)\right)\right) \\ &= A^{(n)}_{ij} \frac{\partial}{\partial {\Sigma_I^{(n)}}^{-1}}\left(-\frac{1}{2}\left(r_{ij}-p^{(n)}\right)^\top{\Sigma_I^{(n)}}^{-1}\left(r_{ij}-p^{(n)}\right)\right) \\ &= -\frac{A^{(n)}_{ij}}{2} \left(r_{ij}-p^{(n)}\right)\left(r_{ij}-p^{(n)}\right)^\top \\ \end{align*}

と計算できる。
元の式は、

\begin{align*} \lambda^{(n)}_{ij} &:= \left( \frac{\partial L}{\partial \bar{T}_{ij}}\frac{\partial \bar{T}_{ij}}{\partial A^{(n)}_{ij}} + \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial A^{(n)}_{ij}} \right) \frac{A^{(n)}_{ij}}{\alpha^{(n)}} \\ &= \left( -\frac{\partial L}{\partial \bar{T}_{ij}} \frac{\bar{T}_{ij}}{1-A^{(n)}_{ij}} + \frac{\partial L}{\partial \bar{P}_{ij}} \frac{1}{1-A^{(n)}_{ij}} \left( P^{(:n)}_{ij} - \bar{P}_{ij} + T^{(:n)}_{ij}C^{(n)}_{ij} \right) \right) \frac{A^{(n)}_{ij}}{\alpha^{(n)}} \\ &= \frac{A^{(n)}_{ij}/\alpha^{(n)}}{1-A^{(n)}_{ij}} \left( -\frac{\partial L}{\partial \bar{T}_{ij}} \bar{T}_{ij} + \frac{\partial L}{\partial \bar{P}_{ij}} \left( P^{(:n)}_{ij} - \bar{P}_{ij} + T^{(:n)}_{ij}C^{(n)}_{ij} \right) \right) \\ &= \frac{\exp\left(-\frac{1}{2}\left(r_{ij}-p^{(n)}\right)^\top{\Sigma_I^{(n)}}^{-1}\left(r_{ij}-p^{(n)}\right)\right)}{1-A^{(n)}_{ij}} \left( -\frac{\partial L}{\partial \bar{T}_{ij}} \bar{T}_{ij} + \frac{\partial L}{\partial \bar{P}_{ij}} \left( P^{(:n)}_{ij} - \bar{P}_{ij} + T^{(:n)}_{ij}C^{(n)}_{ij} \right) \right) \\ \end{align*}

とすることで、

\begin{align*} \frac{\partial L}{\partial \alpha^{(n)}} &= \sum_{ij} \left( \frac{\partial L}{\partial \bar{T}_{ij}}\frac{\partial \bar{T}_{ij}}{\partial A^{(n)}_{ij}} + \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial A^{(n)}_{ij}} \right) \frac{\partial A^{(n)}_{ij}}{\partial \alpha^{(n)}} \\ &= \sum_{ij} \left( \frac{\partial L}{\partial \bar{T}_{ij}}\frac{\partial \bar{T}_{ij}}{\partial A^{(n)}_{ij}} + \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial A^{(n)}_{ij}} \right) \frac{A^{(n)}_{ij}}{\alpha^{(n)}} \\ &= \sum_{ij} \lambda^{(n)}_{ij} \\ \end{align*}

\begin{align*} \frac{\partial L}{\partial p^{(n)}} &= \sum_{ij} \left( \frac{\partial L}{\partial \bar{T}_{ij}}\frac{\partial \bar{T}_{ij}}{\partial A^{(n)}_{ij}} + \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial A^{(n)}_{ij}} \right) \frac{\partial A^{(n)}_{ij}}{\partial p^{(n)}} \\ &= \sum_{ij} \left( \frac{\partial L}{\partial \bar{T}_{ij}}\frac{\partial \bar{T}_{ij}}{\partial A^{(n)}_{ij}} + \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial A^{(n)}_{ij}} \right) A^{(n)}_{ij} \left( {\Sigma_I^{(n)}}^{-1}\left(r_{ij} - p^{(n)}\right) \right)^\top \\ &= \alpha^{(n)} \sum_{ij} \lambda^{(n)}_{ij} \left( {\Sigma_I^{(n)}}^{-1}\left(r_{ij} - p^{(n)}\right) \right)^\top \\ \end{align*}

\begin{align*} \frac{\partial L}{\partial {\Sigma_I^{(n)}}^{-1}} &= \sum_{ij} \left( \frac{\partial L}{\partial \bar{T}_{ij}}\frac{\partial \bar{T}_{ij}}{\partial A^{(n)}_{ij}} + \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial A^{(n)}_{ij}} \right) \frac{\partial A^{(n)}_{ij}}{\partial {\Sigma_I^{(n)}}^{-1}} \\ &= -\sum_{ij} \left( \frac{\partial L}{\partial \bar{T}_{ij}}\frac{\partial \bar{T}_{ij}}{\partial A^{(n)}_{ij}} + \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial A^{(n)}_{ij}} \right) \frac{A^{(n)}_{ij}}{2} \left(r_{ij}-p^{(n)}\right)\left(r_{ij}-p^{(n)}\right)^\top \\ &= -\frac{\alpha^{(n)}}{2} \sum_{ij} \lambda^{(n)}_{ij} \left(r_{ij}-p^{(n)}\right)\left(r_{ij}-p^{(n)}\right)^\top \\ \end{align*}

\begin{align*} \frac{\partial L}{\partial c^{(n)}} &= \sum_{ij} \frac{\partial L}{\partial \bar{P}_{ij}}\frac{\partial \bar{P}_{ij}}{\partial C^{(n)}_{ij}} \\ &= \sum_{ij} \frac{\partial L}{\partial \bar{P}_{ij}} T^{(:n-1)}_{ij}A^{(n)}_{ij} \\ \end{align*}

と表すことができる。

これらの値を計算するには\(n\)ごとの\(T^{(:n)}\)や\(P^{(:n)}\)が必要になるが、forwardで計算したこれらの値を保持し続けるとやはりVRAMを大量に消費してしまうので、実装ではbackwardでもforwardと同様のアルファブレンドの繰り返し処理を行って\(T^{(:n)}, P^{(:n)}\)などの値を計算し直している。

学習

3DGSの学習はニューラルネットワークの学習と同様に、forward (3DGSではレンダリングに相当) 、backward、optimizationを繰り返すループで構成される。
パラメーターの初期化はSfM (Structure from Motion) によって行われる。
また、通常のニューラルネットワークの学習とは異なり、一定ステップごとにGaussianの総数を調整するDensificationという処理が追加で実行される。

3DGSの学習の流れ

なお、公式実装では3DGSの学習はPyTorchを用いて実装されている。
Gaussianの各パラメーターはモデルの重みパラメーターに相当し、モデルの入力はカメラ姿勢、出力はレンダリングされた画像になる。

初期パラメーターの推定

まずは、3DGSを実行するために必要な情報を初期化する。
初期化にはSfM (Structure from Motion) と呼ばれる技術が利用される。SfMでは2次元の画像群を用いてカメラの姿勢 (=位置と角度) と、3D点群を推測することができる。

3DGSにおいてこの初期化の手順は省略可能だが、初期化を行うことによって3DGSの学習を効率化することができるようになる。

COLMAP

COLMAPは2016年に発表されたSfMの実装の一種。

COLMAPでは、まずそれぞれの画像に対してSIFT (Scale-Invariant Feature Transform) を実行する。
SIFTは1枚の画像からDoG (Difference of Gaussian) が極小・極大値を取る全ての点を特徴点として検出し、それぞれの特徴点に対して一定のアルゴリズムに基づいて128次元の周辺情報ベクトル (SIFT特徴量) を計算する。SIFT特徴量は、拡大縮小や回転に対して変動が少なくなるように設計されている。

SIFTの実行例。左は入力画像で、右は検出された点を視覚化した画像。(画像の引用元)

次に、異なる画像から1点ずつ取り出したSIFT特徴量同士を比較し、類似度が高い特徴点は3次元空間上の同じ点から投影されたものとみなす。このような仮定を課すことによって、カメラの姿勢と、特徴点の3次元空間上での位置を表す点群を推定することができるようになる。
より具体的には、COLMAPでは最初に2枚の画像からカメラ姿勢と点群を初期化し、1枚ずつ画像を追加してカメラ姿勢と点群を相互に微調整していく。このように1枚ずつ画像を追加してパラメーターを調整するSfMはIncremental SfMと呼ばれる。

COLMAPの実行結果の例。赤い四角錐はそれぞれ教師画像から推定された撮影位置と方向を表す。

損失関数

Gaussianとカメラ姿勢情報からレンダリングして出力画像を得たとき、対応する真の画像との差を取って損失を計算する。
損失はL1損失 (ピクセルごとの差の絶対値に対する平均) とSSIMの加重平均で実装されている。(公式実装では\(\lambda=0.2\))

\begin{align*} \text{Loss} = (1-\lambda)\cdot\text{L1Loss}(\text{gt}, \text{out}) + \lambda\cdot\text{SSIMLoss}(\text{gt}, \text{out}) \end{align*}

通常のニューラルネットワークの学習と同じように、計算された損失の値は計算グラフを通じて逆伝播 (backward) され、Gaussianの各パラメーターの調整 (optimization) に用いられる。

SSIM損失

SSIM (Structural Similarity Index Measure) は2004年に提案された画像の類似度を評価する指標。
単にピクセル単位で独立した比較を行うのではなく、空間的特徴を捉えることでより人間の知覚に近い比較を行えるように設計された評価指標。

3DGSの実装では比較する2枚の画像\(x,y\)について

\begin{align*} \mathrm{SSIM}(x,y) = \frac{(2\mu_x\mu_y+C_1)(2\sigma_{xy}+C_2)}{(\mu_x^2+\mu_y^2+C_1)(\sigma_x^2+\sigma_y^2+C_2)} \end{align*}

と計算する。
3DGSにおける実装では、平均や分散・共分散は画像全体で取られるのではなく、各ピクセルを中心とした標準偏差1.5 pixelのGaussカーネルによって重み付けされた加重平均で取られる。したがって、SSIMの値はまずは各ピクセルごとに計算され、その全ピクセルに対する平均が最終的な画像全体のSSIMとなる。
定数は\(C_1=0.01^2, C_2=0.03^2\)が用いられる。

L1とSSIMの実行例。左から元の画像、変化後の画像、各ピクセルのL1距離、各ピクセルのSSIMを表す。
上段は明るさを変えた画像に対するL1距離とSSIM。画像全体のL1距離は0.121、画像全体のSSIMは0.856。
下段はぼかしをかけた画像に対するL1距離とSSIM。画像全体のL1距離は0.038、画像全体のSSIMは0.768。
(画像の引用元)

ここで、

\begin{align*} -(\mu_x^2+\mu_y^2) \leq 2\mu_x\mu_y \leq \mu_x^2+\mu_y^2 \end{align*}

なので、

\begin{align*} -1 < -1+\frac{2C_1}{\mu_x^2+\mu_y^2+C_1} \leq \frac{2\mu_x\mu_y+C_1}{\mu_x^2+\mu_y^2+C_1} \leq 1 \end{align*}

となり、またCauchy-Schwarzの不等式より、

\begin{align*} |2\sigma_{xy}| &= 2\left| \mathbb{E}\left((x-\bar{x})(y-\bar{y})\right) \right| \\ &\leq 2\sqrt{\mathbb{E}\left((x-\bar{x})^2\right)\mathbb{E}\left((y-\bar{y})^2\right)} \\ &= 2\sigma_x\sigma_y \\ &= \sigma_x^2+\sigma_y^2 - (\sigma_x-\sigma_y)^2 \\ &\leq \sigma_x^2+\sigma_y^2 \end{align*}

となるので、

\begin{align*} -1 < -1+\frac{2C_2}{\sigma_x^2+\sigma_y^2+C_2} \leq \frac{2\sigma_{xy}+C_2}{\sigma_x^2+\sigma_y^2+C_2} \leq 1 \end{align*}

となる。
したがって、SSIMは\((-1, 1]\)の範囲の値を取る。

全く同じ画像同士の比較では\(\mu_x=\mu_y, \sigma_x^2=\sigma_y^2=\sigma_{xy}\)となることから、

\begin{align*} \mathrm{SSIM}(x,y) &= \frac{(2\mu_x\mu_y+C_1)(2\sigma_{xy}+C_2)}{(\mu_x^2+\mu_y^2+C_1)(\sigma_x^2+\sigma_y^2+C_2)} \\ &= \frac{(2\mu_x^2+C_1)(2\sigma_x^2+C_2)}{(2\mu_x^2+C_1)(2\sigma_x^2+C_2)} \\ &= 1 \end{align*}

となるので、SSIMが1に近いときは画像の類似度が高いことを意味し、SSIMの値が小さくなるほど類似度が低くなることを意味する指標であると捉えることができる。SSIMを損失関数として利用する場合は、\(\text{SSIMLoss}(x,y):=1-\mathrm{SSIM}(x,y)\)を用いて類似度が高いほど0に近い値を取るようにする。

Gaussianの密度調整

勾配降下法による最適化だけではGaussianの総数そのもの増減を行うことはできず、過度にGaussianが密集している領域からGaussianを減らしたり、Gaussianが疎な領域にGaussianを追加したりすることができない。
そこで、学習の一定ステップごとにレンダリングと逆伝播の結果に応じてDensification(Gaussianの複製・分割・削除) を行う。

処理	対象	[開始:終了:間隔]
clone	学習が収束していない小さいGaussian	[600:15000:100]
split	学習が収束していない大きいGaussian	[600:15000:100]
prune	不透明度が低いGaussian 3次元空間あるいは2次元空間で大きすぎるGaussian	[600:15000:100]
opacity reset	全てのGaussian	[0:15000:3000]

なお、AdamなどのOptimizerではパラメーターと同じ大きさのMomentum (慣性情報) を内部に保持しているので、以下に解説するDensificationの処理を行ってパラメーターの総数を変動させた場合、Optimizer内部のMomentumを同じ形に調整する必要がある。またパラメーターの値を直接書き換えた場合も、Optimizerの対応するMomentumを0にリセットする必要がある。

複製・分割

学習が収束していないGaussianに対して、複製 (clone) か分割 (split) を行う。
公式実装では、100ステップごとに、600, 700, … , 14900ステップ目で実行される。(最初のステップを0ステップ目ではなく1ステップ目として数える)

学習が収束していないことの判定には位置微分\(\frac{\partial L}{\partial p^{(n)}}\)を用いる。
Guassianごとにbackwardの計算の途中で得られる位置微分\(\frac{\partial L}{\partial p^{(n)}}\)の大きさ\(\left\|\frac{\partial L}{\partial p^{(n)}}\right\|\)を蓄積し続け、判定処理が行われるまでにforwardでレンダリングされた回数\(N_\text{vis}\)による平均を取った値を用いて、

\begin{align*} \frac{\sum \left\|\frac{\partial L}{\partial p^{(n)}}\right\|}{N_\text{vis}} \geq 0.0002 \end{align*}

となるときに、学習が収束していないGaussianであると判定する。

学習が収束していないと判定されたGaussianは2つのGaussianに置き換えられる。置き換えの具体的な処理は、Gaussianの大きさとシーンの大きさの比較結果に応じて、複製・分割のいずれかに分岐する。
シーンの大きさは、データセットに含まれる全てのカメラ位置\(\{t_k\}_{k=1}^K\)について、その中心座標\(\bar{t}\)と各カメラ位置\(t_k\)の距離の最大値によって\(\text{scene_extent}:=1.1\times\max_k\|t_k-\bar{t}\|\)と定める。
また、Gaussianの大きさ\(S_\text{max}\)は、各Gaussianの共分散行列\(\Sigma\)の最大の固有値の平方根とする。
このとき、

\begin{align*} S_\text{max} \leq 0.01 \times \text{scene_extent} \end{align*}

となるものを小さいGaussianと見なして複製(clone) を行い、そうでない大きいGaussianは分割(split) する。

Gaussianの複製では、元のGaussianを残したまま、全く同じ位置に同じパラメーター\(P, \Sigma, c_{l.m}, \alpha\)を持つGaussianを新たに1個追加する。
なお、元のGaussianはOptimizerのMomentumを維持するが、追加されたGaussianはMomentumに0が設定される。

\begin{align*} \left(P^{(\text{new}),}, \Sigma^{(\text{new})}, c_{l,m}^{(\text{new})}, \alpha^{(\text{new})}\right) \leftarrow \left(P^{(\text{old})}, \Sigma^{(\text{old})}, c_{l,m}^{(\text{old})}, \alpha^{(\text{old})}\right) \end{align*}

Gaussianの分割では、元のGaussianを削除し、元の中心座標周辺に、元のGaussianより小さい2つのGaussianを追加する。
新たな2つのGaussianの中心座標は、元のGaussianの共分散行列を用いて\(\mathcal{N}(P,\Sigma)\)に従って独立に抽出される。
また、新たな2つのGaussianの共分散行列は、元の共分散行列\(\Sigma\)を\(1.6^2=2.56\)で割った値にすることで縮小させる。

\begin{align*} P^{(\text{new},1)} \sim \mathcal{N}(P^{(\text{old})},\Sigma^{(\text{old})}) \\ P^{(\text{new},2)} \sim \mathcal{N}(P^{(\text{old})},\Sigma^{(\text{old})}) \end{align*}

\begin{align*} \left(\Sigma^{(\text{new},1)}, c_{l,m}^{(\text{new},1)}, \alpha^{(\text{new},1)}\right) \leftarrow \left(\frac{\Sigma^{(\text{old})}}{1.6^2}, c_{l,m}^{(\text{old})}, \alpha^{(\text{old})}\right) \\ \left(\Sigma^{(\text{new},2)}, c_{l,m}^{(\text{new},2)}, \alpha^{(\text{new},2)}\right) \leftarrow \left(\frac{\Sigma^{(\text{old})}}{1.6^2}, c_{l,m}^{(\text{old})}, \alpha^{(\text{old})}\right) \end{align*}

削除

透明度の低すぎるGaussianと、巨大すぎるGaussianを削除 (prune) する。
100ステップごとに、600, 700, … , 14900ステップ目で実行される。

次のいずれかを満たすGaussianを削除する。

透明度パラメーターが\(\alpha\)が0.005未満のGaussian
複製・分割と同じ基準で、3次元空間においてシーンの大きさの10%を超える大きさのGaussian
2次元投影した大きさ (=共分散行列の最大固有値の平方根) が、画像の長辺の0.4%程度 (公式実装では\(20/3 = 6.66\ldots\text{px}\)で固定) を一度でも超えたことのあるGaussian
- 2次元投影されたGaussianの大きさはレンダリングするカメラによって変動するので、過去の100ステップ (あるいは最初の600ステップ) の間に一度でも画面内に大きくレンダリングされたことを条件とする

不透明度のリセット

不要な浮遊物を削除する目的で、一定ステップごとに全てのGaussianの不透明度\(\alpha\)を0.01に置き換える。
3000ステップごとに、3000, 6000, 9000, 12000ステップ目で実行される。

この処理自体はGaussianの総数を変更しないが、リセットから100ステップ後に実行される削除処理によって不要なGaussianが除去されるように促す効果がある。

利用方法 (Windows)

Windowsにおける公式実装の使い方を紹介する。

インストール

Git, Python (バージョン3.12で動作を確認) , CUDA (12.6で動作を確認) をインストールしておく。
またBuild Tools for Visual Studio (2022で動作を確認) をページ下部の「Tools for Visual Studio」からダウンロードしてインストールしておく。

任意の場所に3DGSのリポジトリをcloneする。
サブモジュールを含むので--recursiveオプションを付ける。

git clone --recursive https://github.com/graphdeco-inria/gaussian-splatting.git

PyTorchとその他必要なパッケージをインストールする。
(PyTorch 2.9.0以上ではサブモジュールのインストールに失敗する)

cd gaussian-splatting
python -m venv venv
.\venv\Scripts\activate

pip install torch==2.6.0 torchvision==0.21.0 torchaudio==2.6.0 --index-url https://download.pytorch.org/whl/cu126
pip install opencv-python
pip install plyfile
pip install tqdm
pip install submodules/diff-gaussian-rasterization --no-build-isolation
pip install submodules/simple-knn --no-build-isolation
pip install submodules/fused-ssim --no-build-isolation

また、COLMAPのWindows用バイナリー (3.12.6で動作を確認) をダウンロードして任意の場所に展開する。
(3.13.0以降のCOLMAPは3DGSの公式スクリプトでは非対応)

学習

COLMAP

gaussian-splattingのリポジトリに含まれるスクリプトを用いてCOLMAPを実行する。
任意の場所にフォルダーを作り、サブフォルダー「input」に画像を入れる。

<データソース>
├input - COLMAP実行前にここに画像を入れる
├images - COLMAP実行時に自動で作られる
├sparse - COLMAP実行時に自動で作られる
└stereo - COLMAP実行時に自動で作られる

gaussian-splatting/convert.pyを実行する。

python convert.py --colmap_executable <COLMAPの展開先>\colmap-x64-windows-cuda\COLMAP.bat -s <データソース>

実行後、COLMAPの学習結果がデータソースフォルダーのsparseに保存される。

3DGS

gaussian-splatting/train.pyを実行して3DGSの学習を行う。
データソースフォルダーにはCOLMAPのときに用意したものと同じパスを指定すれば良い。

python train.py -s <データソースフォルダー>

環境にもよるが30000ステップの学習には20分ほどを要する。
学習の結果はgaussian-splatting/outputに保存される。

ビューアー

3DGSの学習結果は公式のビューアーで確認できる。

<ビューアーの展開先>\viewers\bin\SIBR_gaussianViewer_app.exe -m <3DGSの出力>

Point viewウィンドウを選択した状態で、QWEASDキーで移動、UIOJKLキーで回転することができる。

3D Gaussian Splatting
2026/02/16 23:02 投稿

目次

概要

パラメーター構造

分散共分散行列

球面調和関数の係数

レンダリング (推論)

点群の平面射影

共分散行列の平面射影

球面調和関数による色の決定

アルファブレンド

逆伝播の実装

学習

初期パラメーターの推定

COLMAP

損失関数

SSIM損失

Gaussianの密度調整

複製・分割

削除

不透明度のリセット

利用方法 (Windows)

インストール

学習

COLMAP

3DGS

ビューアー

参考

3DGS

NeRF

SfM