拡散モデルの確率微分方程式
この記事では拡散モデルの生成過程で使われる様々なアルゴリズムの基礎となる理論を解説する。
関連記事
目次
確率微分方程式 (SDE)
Wiener過程のような確率過程を表す項が含まれる微分方程式を、確率微分方程式(SDE, stochastic differential equation)と言う。
この節ではSDEを定式化し、SDEに対して成り立つ性質を導出する。
Wiener過程
各時間単位\(\Delta t\)ごとに\(x_{t+\Delta t} \sim \mathcal{N}(x_t, \Delta tI)\)と発展する\(d\)次元値の確率過程を考える。
正規分布の再生性によれば、そのような過程の確率分布は以下のように表される。
\begin{align} p(x_t | x_{t - \Delta t}) &= p_\mathcal{N}\left(x_t \middle| x_{t - \Delta t}, \Delta tI\right) \\ p(x_t | x_{t - 2\Delta t}) &= p_\mathcal{N}\left(x_t \middle| x_{t - 2\Delta t}, 2\Delta tI\right) \\ p(x_t | x_{t - 3\Delta t}) &= p_\mathcal{N}\left(x_t \middle| x_{t - 3\Delta t}, 3\Delta tI\right) \\ &\vdots \\ p(x_t | x_{t - N\Delta t}) &= p_\mathcal{N}\left(x_t \middle| x_{t - N\Delta t}, N\Delta tI\right) \\ \end{align}
\(s := t - N\Delta t\)とすると、以下のように表すことができる。
\begin{align} p(x_t | x_s) &= p_\mathcal{N}\left(x_t \middle| x_s, (t-s)I\right) \\ \end{align}
この過程に対して\(\Delta t \rightarrow 0\)と極限を取ったものをWiener過程(Brown運動)\(w_t\)と呼ぶ。
初期値が0であるという条件も加え、Wiener過程は以下のように定義される。
\begin{align} w_0 &= 0 \\ w_t - w_s &\sim \mathcal{N}\left(0, (t-s)I\right) \qquad (t \geq s) \end{align}
\(\varepsilon \sim \mathcal{N}(0, I)\)に対して、\(w_t - w_s = \sqrt{t-s}\varepsilon\)と表すこともできる。
ここで、\(s\rightarrow t-dt\)とすると、
\begin{align} dw_t = w_t - w_{t-dt} = \sqrt{dt}\varepsilon \end{align}
となり、\(dw_t\)は\(\sqrt{dt}\)のスケールを持つ量と解釈することができる。
一般のSDEは、Wiener過程の項を持つ以下の表記で表される。
\begin{align} dx_t = f(x_t, t)dt + g(x_t, t)dw_t \end{align}
\(f(x_t, t)\)のことをドリフト係数(drift coefficient)、\(g(x_t, t)\)のことを拡散係数(diffusion coefficient)と呼ぶ。
一般には\(f(x_t, t)\in R^d\)はベクトル値であり、\(g(x_t, t)\in R^{d\times d}\)は行列値である。ただし、この記事では\(g\)は行列値ではなく1次元の実数値\(g(x_t, t)\in R\)を返すものとして計算を簡略化する。
右辺の中で\(\sqrt{dt}\)に相当する\(w_t\)と\(dt\)が混在していて奇妙にも感じられるが、これは本来は分布の平均と分散の2つの値がそれぞれ発展しているのを、表記を簡単にするために無理やり1行で表したものである。
例えるならば、実部と虚部を1行で表す複素数と似たものであると捉えるとわかりやすいかもしれない。
Fokker-Planck方程式
SDE
\begin{align} dx_t = f(x_t, t)dt + g(x_t, t)dw_t \end{align}
によって発展する\(x_t\)が従う分布を\(p_t(x)\)と表す。
(微分可能性などのある程度の条件を満たす範囲で)任意の関数\(a: R^d\rightarrow R\)を取る。
\(a(x)\)の期待値を\(t\)で微分すると以下の結果が得られる。
\begin{align} \frac{d}{dt}\mathbb{E}_{p_t}\left(a(x)\right) &= \frac{d}{dt}\int a(x)p_t(x)dx \\ &= \int a(x)\frac{\partial p_t(x)}{\partial t}dx \\ \end{align}
一方、時刻\(t+dt\)の分布\(p_{t+dt}(x)\)に従って取り出した値\(x\)は、時刻\(t\)の分布\(p_{t}(x)\)に従って取り出した値をSDEによって時間発展させたものと考えることもできる。時間発展させることによりWiener過程の確率変数\(\varepsilon\)が追加で発生することに注意して、Taylor展開を用いて以下のように式を変形する。
\begin{align} \frac{d}{dt}\mathbb{E}_{p_t}\left(a(x)\right) &= \frac{1}{dt}\left( \mathbb{E}_{p_{t+dt}}\left(a(x)\right) - \mathbb{E}_{p_t}\left(a(x)\right) \right) \\ &= \frac{1}{dt}\left( \mathbb{E}_{p_{t}(x_t),\varepsilon}\left(a(x_t+dx_t)\right) - \mathbb{E}_{p_t}\left(a(x_t)\right) \right) \\ &= \frac{1}{dt}\mathbb{E}_{p_{t}(x_t),\varepsilon}\left( a(x_t+dx_t) - a(x_t) \right) \\ &= \frac{1}{dt}\mathbb{E}_{p_{t}(x_t),\varepsilon}\left( \sum_{i=1}^{d}\frac{\partial a(x_t)}{\partial x_i}dx_{t,i} + \frac{1}{2}\sum_{i,j=1}^{d}\frac{\partial^2 a(x_t)}{\partial x_i\partial x_j}dx_{t,i}dx_{t,j} + \mathcal{O}(|dx|^4) \right) \\ \end{align}
\(dx_{t,i}\)にSDEを代入する。(\(f,g\)の引数は省略している)
\begin{align} \frac{d}{dt}\mathbb{E}_{p_t}\left(a(x)\right) &= \frac{1}{dt}\mathbb{E}_{p_{t}(x_t),\varepsilon}\left( \sum_{i=1}^{d}\frac{\partial a(x_t)}{\partial x_i}dx_{t,i} + \frac{1}{2}\sum_{i,j=1}^{d}\frac{\partial^2 a(x_t)}{\partial x_i\partial x_j}dx_{t,i}dx_{t,j} + \mathcal{O}(|dx|^3) \right) \\ &= \frac{1}{dt}\mathbb{E}_{p_{t}(x_t),\varepsilon}\left( \sum_{i}\frac{\partial a(x_t)}{\partial x_i}\left( f_i dt+g\sqrt{dt}\varepsilon_i \right) + \frac{1}{2}\sum_{i,j}\frac{\partial^2 a(x_t)}{\partial x_i\partial x_j}\left( f_i dt+g\sqrt{dt}\varepsilon_i \right)\left( f_j dt+g\sqrt{dt}\varepsilon_j \right) + \mathcal{O}(|dx|^3) \right) \\ &= \frac{1}{dt}\mathbb{E}_{p_{t}(x_t),\varepsilon}\left( \sum_{i}\frac{\partial a(x_t)}{\partial x_i}\left( f_i dt+g\sqrt{dt}\varepsilon_i \right) + \frac{1}{2}\sum_{i,j}\frac{\partial^2 a(x_t)}{\partial x_i\partial x_j}g^2 dt\varepsilon_i \varepsilon_j + \mathcal{O}(dt^{3/2}) \right) \\ \end{align}
\(\varepsilon\)に対しての期待値を取ると、
\begin{align} \mathbb{E}(\varepsilon_i) &= 0 \\ \mathbb{E}(\varepsilon_i^2) &= 1 \\ \mathbb{E}(\varepsilon_i \varepsilon_j) &= 0 \quad (i\neq j) \\ \end{align}
となるので、
\begin{align} \frac{d}{dt}\mathbb{E}_{p_t}\left(a(x)\right) &= \frac{1}{dt}\mathbb{E}_{p_{t}(x_t),\varepsilon}\left( \sum_{i}\frac{\partial a(x_t)}{\partial x_i}\left( f_i dt+g\sqrt{dt}\varepsilon_i \right) + \frac{1}{2}\sum_{i,j}\frac{\partial^2 a(x_t)}{\partial x_i\partial x_j}g^2 dt\varepsilon_i \varepsilon_j + \mathcal{O}(dt^{3/2}) \right) \\ &= \frac{1}{dt}\mathbb{E}_{p_{t}(x_t)}\left( \sum_{i}\frac{\partial a(x_t)}{\partial x_i}f_i dt + \frac{1}{2}\sum_{i}\frac{\partial^2 a(x_t)}{\partial x_i^2}g^2 dt + \mathcal{O}(dt^{3/2}) \right) \\ &= \mathbb{E}_{p_{t}(x_t)}\left( \sum_{i} \left( \frac{\partial a(x_t)}{\partial x_i}f_i + \frac{1}{2}\frac{\partial^2 a(x_t)}{\partial x_i^2}g^2 \right) \right) + \mathcal{O}(dt^{1/2}) \\ &= \int p_t(x_t)\sum_{i} \left( \frac{\partial a(x_t)}{\partial x_i}f_i + \frac{1}{2}\frac{\partial^2 a(x_t)}{\partial x_i^2}g^2 \right)dx_t + \mathcal{O}(dt^{1/2}) \\ \end{align}
最終的に残った\(\mathcal{O}(dt^{1/2})\)は\(dt\rightarrow 0\)で\(0\)になるので削除する。
また、\(x_{t,i}\rightarrow \pm\infty\)のとき\(p_t(x_t)\rightarrow 0, \nabla p_t(x_t)\rightarrow 0\)となるので、部分積分を利用して以下のように変形できる。
\begin{align} \frac{d}{dt}\mathbb{E}_{p_t}\left(a(x)\right) &= \int p_t(x_t)\sum_{i} \left( \frac{\partial a(x_t)}{\partial x_i}f_i + \frac{1}{2}\frac{\partial^2 a(x_t)}{\partial x_i^2}g^2 \right)dx_t + \mathcal{O}(dt^{1/2}) \\ &= \int \sum_{i} \left( -a(x_t)\frac{\partial }{\partial x_i}\left(p_t(x_t)f_i\right) + \frac{1}{2}a(x_t)\frac{\partial^2}{\partial x_i^2}\left(p_t(x_t)g^2\right) \right)dx_t \\ &= \int a(x_t)\sum_{i} \left( -\frac{\partial }{\partial x_i}\left(p_t(x_t)f_i\right) + \frac{1}{2}\frac{\partial^2}{\partial x_i^2}\left(p_t(x_t)g^2\right) \right)dx_t \\ &= \int a(x_t)\left( -\nabla \cdot \left(p_t(x_t)f(x_t, t)\right) + \frac{1}{2}\Delta \left(p_t(x_t)g(x_t, t)^2\right) \right)dx_t \\ &= \int a(x)\left( -\nabla \cdot \left(p_t(x)f(x, t)\right) + \frac{1}{2}\Delta \left(p_t(x)g(x, t)^2\right) \right)dx \\ \end{align}
ここで、\(\Delta = \nabla \cdot \nabla\)はLaplace作用素。
最初に\(\frac{d}{dt}\mathbb{E}_{p_t}\left(a(x)\right) = \int a(x)\frac{\partial p_t(x)}{\partial t}dx \)という別の計算結果を求めていたが、\(a\)が任意の関数であることを考慮すると以下の関係を導くことができる。
\begin{align} \frac{\partial p_t(x)}{\partial t} = -\nabla \cdot \left(p_t(x)f(x, t)\right) + \frac{1}{2}\Delta \left(p_t(x)g(x, t)^2\right) \end{align}
\(p_t\)に関するこの方程式をFokker-Planck方程式と呼ぶ。
probability flow ODE
Fokker-Planck方程式を更に変形していく。
\begin{align} \frac{\partial p_t(x)}{\partial t} &= -\nabla \cdot \left(p_t(x)f(x, t)\right) + \frac{1}{2}\Delta \left(p_t(x)g(x, t)^2\right) \\ &= -\nabla \cdot \left(p_t(x)f(x, t) - \frac{1}{2}\nabla \left(p_t(x)g(x, t)^2\right)\right) \\ &= -\nabla \cdot \left(p_t(x)f(x, t) - p_t(x)g(x, t)\nabla g(x, t) - \frac{1}{2}g(x, t)^2\nabla p_t(x)\right) \\ &= -\nabla \cdot \left(p_t(x)f(x, t) - p_t(x)g(x, t)\nabla g(x, t) - p_t(x)\frac{1}{2}g(x, t)^2\nabla \log p_t(x)\right) \\ &= -\nabla \cdot \left(p_t(x)\left(f(x, t) - g(x, t)\nabla g(x, t) - \frac{1}{2}g(x, t)^2\nabla \log p_t(x)\right)\right) \\ &=: -\nabla \cdot \left(p_t(x)\bar{f}(x, t)\right) \\ \end{align}
したがって、
\begin{align} \begin{cases} \bar{f}(x, t) &:= f(x, t) - g(x, t)\nabla g(x, t) - \frac{1}{2}g(x, t)^2\nabla \log p_t(x) \\ \bar{g}(x, t) &:= 0 \\ \end{cases} \end{align}
とすれば、
\begin{align} \frac{\partial p_t(x)}{\partial t} &= -\nabla \cdot \left(p_t(x)\bar{f}(x, t)\right) + \frac{1}{2}\Delta \left(p_t(x)\bar{g}(x, t)^2\right) \end{align}
となる。
つまり、
\begin{align} \begin{cases} dx_t = f(x_t, t)dt + g(x_t, t)dw_t \\ dx_t = \bar{f}(x_t, t)dt + \bar{g}(x_t, t)dw_t \end{cases} \end{align}
という2つの異なるSDEから同じFokker-Planck方程式が導かれることとなり、SDEの解\(p_t(x)\)が全く同じ分布になることがわかる。
ここで、
\begin{align} dx_t &= \bar{f}(x_t, t)dt + \bar{g}(x_t, t)dw_t \\ &= \left(f(x_t, t) - g(x_t, t)\nabla g(x_t, t) - \frac{1}{2}g(x_t, t)^2\nabla \log p_t(x_t)\right)dt \end{align}
にはもはやWiener項は存在せず、確率微分方程式ではなく常微分方程式(ODE)となっていることがわかる。このように導かれたODEのことをprobability flow ODEと呼ぶ。
拡散モデルでは特に\(g(x_t,t)=g(t)\)である場合のみを考える。その場合のprobability flow ODEは以下。
\begin{align} dx_t &= \left(f(x_t, t) - \frac{1}{2}g(t)^2\nabla \log p_t(x_t)\right)dt \end{align}
また、任意の関数\(h(t)\)を用いて、
\begin{align} dx_t = \left(f(x_t, t) - \frac{1}{2}g(t)^2\nabla \log p_t(x_t)\right)dt + \frac{1}{2}h(t)^2\nabla \log p_t(x_t)dt + h(t)dw_t \end{align}
と定めたSDEも同じFokker-Planck方程式に帰着することがわかる。
このSDEは\(h\)の自由度を持つことから、元のSDEの一般化と見ることができる。
拡散モデルでは\(\nabla\log p_t(x_t)\)はスコアと呼ばれる。
\begin{align} \begin{cases} dx_t &= f(x_t, t)dt + g(t)dw_t \qquad \text{(SDE)} \\ dx_t &= \left(f(x_t, t) - \frac{1}{2}g(t)^2\nabla \log p_t(x_t)\right)dt \qquad \text{(probability flow ODE)} \\ dx_t &= \left(f(x_t, t) - \frac{1}{2}g(t)^2\nabla \log p_t(x_t)\right)dt + \frac{1}{2}h(t)^2\nabla \log p_t(x_t)dt + h(t)dw_t \qquad \text{(generalized SDE)} \\ \end{cases} \end{align}
以下の動画を用いて、Probability Flowについてより具体的に説明する。
Stable Diffusionのノイズスケジュールに従う1次元の拡散モデルを前提とする。
青色のグラフは各時刻における確率分布\(p_t(x_t)\)を表す。拡散過程によってグラフは標準正規分布\(p_\mathcal{N}(x_t|0,I)\)に近付くことがわかる。
赤色の点は各時刻において累積分布が等間隔に分割されるようサンプルした10個の点である。つまり、赤色の点によって区切られたそれぞれの区間で\(p_t(x_t)\)を積分すると\(1/11\)になる。
赤い点が辿る軌跡を薄い赤色の線で表しているが、この軌跡こそがProbability Flowである。また、Probability Flow ODEとは、Probability Flowに沿って変化する\(x_t\)が従う方程式のことである。
reverse-time SDE
SDEは前方にしか時間発展できないので、そのままでは生成過程に用いることはできない。
一方、ODEは\(t\)にしか依存しないので後方への時間発展も考えることができる。このことを利用して、時間後方へ発展するSDEを導出する。
\(s:=-t, \bar{x}_s:=x_t\)とし、\(\bar{f}, \bar{g}, \bar{p}_s\)なども同様に定める。
\begin{align} d\bar{x}_s = dx_t &= \left(f(x_t, t) - \frac{1}{2}g(t)^2\nabla \log p_t(x_t)\right)dt \\ &= \left(\bar{f}(\bar{x}_s, s) - \frac{1}{2}\bar{g}(s)^2\nabla \log \bar{p}_s(\bar{x}_s)\right)\frac{dt}{ds}ds \\ &= \left(-\bar{f}(\bar{x}_s, s) + \frac{1}{2}\bar{g}(s)^2\nabla \log \bar{p}_s(\bar{x}_s)\right)ds \\ \end{align}
このODEに対応する一般化SDEは以下。
\begin{align} d\bar{x}_t &= \left(-\bar{f}(\bar{x}_s, s) + \frac{1}{2}\bar{g}(s)^2\nabla \log \bar{p}_s(\bar{x}_s)\right)ds + \frac{1}{2}\bar{h}(s)^2\nabla \log \bar{p}_s(\bar{x}_s)ds + \bar{h}(s)d\bar{w}_s \\ \end{align}
ここで、\(d\bar{w}_s\)は後ろ向きにのみ時間発展するWiener過程。
この一般化SDEの時間を再び\(t\)に戻す。(ただし、\(d\bar{w}_t = d\bar{w}_s\)と表す)
\begin{align} dx_t &= \left(f(x_t, t) - \frac{1}{2}g(t)^2\nabla \log p_t(x_t)\right)dt - \frac{1}{2}h(t)^2\nabla \log p_t(x_t)dt + h(t)d\bar{w}_t \\ \end{align}
このように、後ろ向きにのみ時間発展するWiener過程で表したSDEをreverse-time SDEと呼ぶ。
特に、\(h=g\)とすることで以下の特殊な形が得られる。
\begin{align} dx_t &= \left(f(x_t, t) - g(t)^2\nabla \log p_t(x_t)\right)dt + g(t)d\bar{w}_t \\ \end{align}
\begin{align} \begin{cases} dx_t &= \left(f(x_t, t) - g(t)^2\nabla \log p_t(x_t)\right)dt + g(t)d\bar{w}_t \qquad \text{(reverse-time SDE)} \\ dx_t &= \left(f(x_t, t) - \frac{1}{2}g(t)^2\nabla \log p_t(x_t)\right)dt - \frac{1}{2}h(t)^2\nabla \log p_t(x_t)dt + h(t)d\bar{w}_t \qquad \text{(generalized reverse-time SDE)} \\ \end{cases} \end{align}
また、順方向のSDEと比較すると、
\begin{align} \begin{cases} dx_t &= f(x_t, t)dt + g(t)dw_t \\ dx_t &= f(x_t, t)dt + g(t)\left(- g(t)\nabla \log p_t(x_t)dt + d\bar{w}_t\right) \\ \end{cases} \end{align}
となるので、
\begin{align} d\bar{w}_t = dw_t + g(t)\nabla \log p_t(x_t)dt \end{align}
という関係を得ることもできる。
時刻0の値で条件付けられた分布
\(f(x_t, t)=f(t)x_t\)となる場合を考える。
\begin{align} dx_t = f(t)x_tdt + g(t)dw_t \end{align}
\(w_t\)の項を一旦無視すると、以下のODEになる。
\begin{align} dx_t = f(t)x_tdt \end{align}
このODEは容易に解くことができ、その解は以下。
\begin{align} x_t = x_0\exp\left(\int_0^t f(s)ds\right) \end{align}
ここで定数変化法を用いる。
\begin{align} x_t = y_t\exp\left(\int_0^t f(s)ds\right) \end{align}
として、元のSDEを代入する。
\begin{align} dy_t &= d\left(x_t\exp\left(-\int_0^t f(s)ds\right)\right) \\ &= dx_t\exp\left(-\int_0^t f(s)ds\right) - f(t)x_t\exp\left(-\int_0^t f(s)ds\right)dt \\ &= \left(dx_t - f(t)x_tdt\right)\exp\left(-\int_0^t f(s)ds\right) \\ &= g(t)\exp\left(-\int_0^t f(s)ds\right)dw_t \\ \end{align}
したがって、
\begin{align} y_t &\sim \mathcal{N}\left(y_0, \int_0^t g(s)^2\exp\left(-2\int_0^s f(r)dr\right) ds \right) \end{align}
となり、\(x_t\)の分布に戻すと以下のようになる。
\begin{align} x_t &\sim \mathcal{N}\left(\exp\left(\int_0^t f(s)ds\right)x_0, \exp\left(2\int_0^t f(s)ds\right) \int_0^t g(s)^2\exp\left(-2\int_0^s f(r)dr\right) ds I \right) \end{align}
したがって、
\begin{align} \begin{cases} \alpha(t) &:= \exp\left(\int_0^t f(s)ds\right) \\ \sigma(t)^2 &:= \alpha(t)^2 \int_0^t \frac{g(s)^2}{\alpha(s)^2} ds \\ \end{cases} \end{align}
とすると、
\begin{align} x_t &\sim \mathcal{N}\left(\alpha(t)x_0, \sigma(t)^2 I \right) \end{align}
となる。
\(f(x_t, t)=f(t)x_t\)のとき、
\begin{align} \begin{cases} x_t &\sim \mathcal{N}\left(\alpha(t)x_0, \sigma(t)^2 I \right) \\ \alpha(t) &:= \exp\left(\int_0^t f(s)ds\right) \\ \sigma(t)^2 &:= \alpha(t)^2 \int_0^t \frac{g(s)^2}{\alpha(s)^2} ds \\ \end{cases} \end{align}
\(t=0\)のときは特に次の式が成り立つ。
\begin{align} \begin{cases} \alpha(0) &= \exp\left(0\right) = 1 \\ \sigma(0)^2 &= 0 \\ \end{cases} \end{align}
また、
\begin{align} \frac{\sigma(t)^2}{\alpha(t)^2} = \int_0^t \frac{g(s)^2}{\alpha(s)^2} ds \end{align}
は積分の中身が常に非負なので単調増加である。(つまり\(\mathrm{SNR}(t)=\alpha(t)^2/\sigma(t)^2\)は単調減少)
逆に、\(\alpha(t), \sigma(t)\)が与えられているとき以下のようにSDEを得ることができる。
\begin{align} f(t) &= \frac{\alpha'(t)}{\alpha(t)} \\ g(t) &= \sqrt{\alpha(t)^2\frac{d}{dt}\frac{\sigma(t)^2}{\alpha(t)^2}} \\ \end{align}
拡散過程が\(x_t \sim \mathcal{N}\left(\alpha(t)x_0, \sigma(t)^2 I \right)\)に従うとき、以下のSDEもまた同じ分布に従う。
\begin{align} dx_t = \frac{\alpha'(t)}{\alpha(t)}x_tdt + \sqrt{\alpha(t)^2\frac{d}{dt}\frac{\sigma(t)^2}{\alpha(t)^2}}dw_t \end{align}
また、PF-ODEは次のようになる。
\begin{align} \frac{dx_t}{dt} = \frac{\alpha'(t)}{\alpha(t)}x_t - \frac{1}{2}\alpha(t)^2\frac{d}{dt}\frac{\sigma(t)^2}{\alpha(t)^2}\nabla \log p_t(x_t) \end{align}
DDPMのSDE
この節では、DDPMの拡散過程を連続化することでSDEを導出する流れを解説する
係数の連続化
DDPMでは各タイムステップの拡散過程を以下のように定め、タイムステップの総数は\(T=1000\)としていた。
\begin{align} x_{t+1} = \sqrt{1-\beta_t}x_t + \sqrt{\beta_t}\varepsilon \end{align}
\(t\)を\(\{0, \cdots, T\}\)から\([0, 1]\)の範囲にスケール変換し、\(T\rightarrow \infty\)とすることでこの過程を連続化してみる。
SDE \(dx_t = f(x_t,t)dt+g(t)dw_t\)と照らし合わせると、\(\sqrt{\beta_t}\)は\(\Delta t=1/T\)のスケールを持っていなければならないことがわかる。
\begin{align} \sqrt{\beta_t} &= \sqrt{T\beta_t\frac{1}{T}} \\ &= \sqrt{T\beta_t\Delta t} \\ \end{align}
となるので、最大タイムステップが\(T\)のときの\(\beta_t\)を\(\beta^{(T)}_t\)と表すと、\(T\rightarrow\infty\)のとき連続化した\(\beta:[0,1]\rightarrow R\)を次のように定めることにする。
\begin{align} \beta(t) &\sim T\beta_{Tt}^{(T)} \end{align}
\(\beta(t)\)は常に有限の値を取る。これはつまり、\(T\)が増えるにつれて、\(\beta^{(T)}_t\)の値は反比例して小さくなっていくことを意味する。
例えばSD (Stable Diffusion)の場合は\(T=1000\)であり、
\begin{align} \beta_t = \left(\sqrt{0.00085}+(\sqrt{0.012}-\sqrt{0.00085})\frac{t-1}{T-1}\right)^2 \end{align}
と定められていた。
\(T=1000\)のときの値を維持するように連続化すると、
\begin{align} \beta(t) = T\beta_{Tt} &= \left(\sqrt{0.00085T}+(\sqrt{0.012T}-\sqrt{0.00085T})\frac{Tt-1}{T-1}\right)^2 \\ &= \left(\sqrt{0.85}+(\sqrt{12}-\sqrt{0.85})\frac{1000t-1}{999}\right)^2 \\ &= \left((\sqrt{12}-\sqrt{0.85})\frac{1000}{999}t + \sqrt{0.85}-\frac{\sqrt{12}-\sqrt{0.85}}{999}\right)^2 \\ &=: \left(at + b\right)^2 \\ \end{align}
とすることで連続化できる。ここで各係数は以下のように定める。
\begin{align} \begin{cases} a &:= (\sqrt{12}-\sqrt{0.85})\frac{1000}{999} \\ b &:= \sqrt{0.85}-\frac{\sqrt{12}-\sqrt{0.85}}{999} \\ \end{cases} \end{align}
SDEの導出
連続化した\(\beta\)を用いて、拡散過程は次のように変形できる。(離散の\(x\)と連続の\(x\)を区別するために括弧を使っている)
\begin{align} x(t+dt) = x_{t+1} &= \sqrt{1-\beta_t}x_t + \sqrt{\beta_t}\varepsilon \\ &= \sqrt{1-T\beta_t\frac{1}{T}}x_t + \sqrt{T\beta_t\frac{1}{T}}\varepsilon \\ &\sim \sqrt{1-\beta(t)dt}x(t) + \sqrt{\beta(t)dt}\varepsilon \\ &= \sqrt{1-\beta(t)dt}x(t) + \sqrt{\beta(t)}dw(t) \\ &= \left(1 - \frac{1}{2}\beta(t)dt + \mathcal{O}(dt^2)\right)x(t) + \sqrt{\beta(t)}dw(t) \\ &= x(t) - \frac{1}{2}\beta(t)x(t)dt + \sqrt{\beta(t)}dw(t) + \mathcal{O}(dt^2) \\ \end{align}
したがって、
\begin{align} dx(t) = -\frac{1}{2}\beta(t)x(t)dt + \sqrt{\beta(t)}dw(t) \\ \end{align}
となり、\(f(t)=-\frac{1}{2}\beta(t), g(t)=\sqrt{\beta(t)}\)のSDEで表すことができた。
\(\alpha(t), \sigma(t)\)はそれぞれ以下のように求めることができる。
\begin{align} \alpha(t) &= \exp\left(\int_0^t f(s)ds\right) \\ &= \exp\left(-\frac{1}{2}\int_0^t \beta(s)ds\right) \\ \end{align}
\begin{align} \sigma(t)^2 &= \alpha(t)^2\int_0^t \frac{g(s)^2}{\alpha(s)^2} ds \\ &= \alpha(t)^2\int_0^t \frac{\beta(s)}{\alpha(s)^2} ds \\ &= \alpha(t)^2\int_0^t \frac{-2\frac{\alpha'(s)}{\alpha(s)}}{\alpha(s)^2} ds \\ &= \alpha(t)^2\int_0^t \frac{-2\alpha'(s)}{\alpha(s)^3} ds \\ &= \alpha(t)^2\left[\frac{1}{\alpha(s)^2}\right]_0^t \\ &= \alpha(t)^2\left(\frac{1}{\alpha(t)^2} - \frac{1}{\alpha(0)^2}\right) \\ &= 1 - \alpha(t)^2 \\ \end{align}
よって、\(\alpha(t)^2+\sigma(t)^2=1\)の関係は自動的に満たされることがわかる。
SDの場合、
\begin{align} \begin{cases} \beta(t) &= \left(at + b\right)^2 \\ a &:= (\sqrt{12}-\sqrt{0.85})\frac{1000}{999} \\ b &:= \sqrt{0.85}-\frac{\sqrt{12}-\sqrt{0.85}}{999} \\ \end{cases} \end{align}
と連続化していたので、\(\alpha(t)\)は以下のように求めることができる。
\begin{align} \alpha(t) &= \exp\left(\int_0^t f(s)ds\right) \\ &= \exp\left(-\frac{1}{2}\int_0^t \beta(s)ds\right) \\ &= \exp\left(-\frac{1}{2}\int_0^t \left(as + b\right)^2ds\right) \\ &= \exp\left(-\frac{1}{6a}\left[\left(as + b\right)^3\right]_0^t\right) \\ &= \exp\left(-\frac{1}{6a}\left(\left(at + b\right)^3-b^3\right)\right) \\ \end{align}
SDの離散の\(\alpha_t^2\)と連続化した\(\alpha(t)^2\)を比較すると、下図のようにほぼ完全に一致することがわかる。
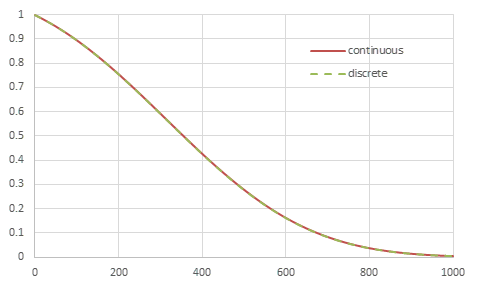
SDの離散の\(\alpha_t^2\)と連続化した\(\alpha(Tt)^2\)
スコアと予測ノイズの関係
スコア\(\nabla\log p_t(x_t)\)をより詳しく見ると、次のように期待値の形で表すことができる。
\begin{align} \nabla_{x_t}\log p_t(x_t) &= \frac{\nabla_{x_t} p_t(x_t)}{p_t(x_t)} \\ &= \frac{1}{p_t(x_t)}\nabla_{x_t} \int q(x_t|x_0)p(x_0) dx_0 \\ &= \frac{1}{p_t(x_t)}\int p(x_0)\nabla_{x_t}q(x_t|x_0) dx_0 \\ &= \frac{1}{p_t(x_t)}\int p(x_0)\nabla_{x_t}p_\mathcal{N}(x_t|\alpha_tx_0,\sigma_t^2I) dx_0 \\ &= \frac{1}{p_t(x_t)}\int p(x_0)\left(-\frac{x_t-\alpha_tx_0}{\sigma_t^2}\right)q(x_t|x_0) dx_0 \\ &= -\frac{1}{\sigma_t}\int \frac{x_t-\alpha_tx_0}{\sigma_t}\frac{p(x_0)q(x_t|x_0)}{p_t(x_t)} dx_0 \\ &= -\frac{1}{\sigma_t}\mathbb{E}_{x_0|x_t}\left(\frac{x_t-\alpha_tx_0}{\sigma_t}\right) \\ \end{align}
一方、DDPMでは\(\varepsilon_\theta(x_t,t)\)を以下の損失を最小化するように求めていた。
\begin{align} Loss = \mathbb{E}_{x_0,t,\varepsilon}\left( \right\| \varepsilon_\theta\left(\alpha_t x_0+\sigma_t\varepsilon\right) - \varepsilon \left\|^2 \right) \end{align}
この損失は、
\begin{align} Loss &= \mathbb{E}_{x_0,t,\varepsilon}\left( \left\| \varepsilon_\theta\left(\alpha_t x_0+\sigma_t\varepsilon,t\right) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,x_t}\left( \left\| \varepsilon_\theta\left(x_t,t\right) - \frac{x_t-\alpha_tx_0}{\sigma_t} \right\|^2 \right) \\ &= \mathbb{E}_{t,x_t}\left( \mathbb{E}_{x_0|x_t}\left( \left\| \varepsilon_\theta\left(x_t,t\right) - \frac{x_t-\alpha_tx_0}{\sigma_t} \right\|^2 \right) \right) \\ &= \mathbb{E}_{t,x_t}\left( \mathbb{E}_{x_0|x_t}\left( \left\| \varepsilon_\theta\left(x_t,t\right) \right\|^2 - 2\varepsilon_\theta\left(x_t,t\right)\cdot\frac{x_t-\alpha_tx_0}{\sigma_t} + \left\| \frac{x_t-\alpha_tx_0}{\sigma_t} \right\|^2 \right) \right) \\ &= \mathbb{E}_{t,x_t}\left( \left\| \varepsilon_\theta\left(x_t,t\right) \right\|^2 -2\varepsilon_\theta\left(x_t,t\right)\cdot\mathbb{E}_{x_0|x_t}\left( \frac{x_t-\alpha_tx_0}{\sigma_t} \right) + \mathbb{E}_{x_0|x_t}\left( \left\| \frac{x_t-\alpha_tx_0}{\sigma_t} \right\|^2 \right) \right) \\ &= \mathbb{E}_{t,x_t}\left( \left\| \varepsilon_\theta\left(x_t,t\right) - \mathbb{E}_{x_0|x_t}\left( \frac{x_t-\alpha_tx_0}{\sigma_t} \right) \right\|^2 - \left\| \mathbb{E}_{x_0|x_t}\left( \frac{x_t-\alpha_tx_0}{\sigma_t} \right) \right\|^2 + \mathbb{E}_{x_0|x_t}\left( \left\| \frac{x_t-\alpha_tx_0}{\sigma_t} \right\|^2 \right) \right) \\ &= \mathbb{E}_{t,x_t}\left( \left\| \varepsilon_\theta\left(x_t,t\right) - \mathbb{E}_{x_0|x_t}\left( \frac{x_t-\alpha_tx_0}{\sigma_t} \right) \right\|^2 \right) + C \\ \end{align}
と表すこともできる。(\(C\)は\(\theta\)によらない定数)
したがって、十分学習されたDDPMでは次のようになることがわかる。
\begin{align} \varepsilon_\theta\left(x_t,t\right) \sim \mathbb{E}_{x_0|x_t}\left( \frac{x_t-\alpha_tx_0}{\sigma_t} \right) \end{align}
これをスコアで表すと次のようになり、スコア\(\nabla\log p_t(x_t)\)と予測ノイズ\(\varepsilon_\theta(x_t,t)\)の間に簡単な関係があることがわかる。
\begin{align} \varepsilon_\theta\left(x_t,t\right) &\sim \mathbb{E}_{x_0|x_t}\left( \frac{x_t-\alpha_tx_0}{\sigma_t} \right) \\ &= -\sigma_t\nabla_{x_t}\log p_t(x_t) \end{align}
α, σによるSDEの分類
拡散過程では一般に
\begin{align} x_t = \alpha_t x_0 + \sigma_t \varepsilon \end{align}
という関係が成り立つ。(ただし、\(\alpha_0=1, \sigma_0=0\))
\(\alpha_t, \sigma_t\)の振る舞いを調べることによって、SDEは次のように分類することができる。

α, σによるSDEの分類 (\(\lambda_t=\log\mathrm(t)=\log\frac{\alpha_t^2}{\sigma_t^2}\))
| 名称 | SDE | \(\alpha_t, \sigma_t\)の関係 | \(\varsigma_t\)で表される\(\alpha_t\) |
|---|---|---|---|
| VE SDE | \(dx_t=g(t)dw_t\) | \(\alpha_t=1\) | \(\alpha_t=1\) |
| VP SDE | \(dx_t=-\frac{1}{2}\beta(t)x_tdt + \sqrt{\beta(t)}dw_t\) | \(\sigma_t^2=1-\alpha_t^2\) | \(\alpha_t=\frac{1}{\sqrt{1+\varsigma_t^2}}\) |
| sub-VP SDE | \(dx_t = -\frac{1}{2}\beta(t)x_tdt + \sqrt{\beta(t)\left( 1-\exp\left(-2\int_0^t\beta(s)ds\right) \right)}dw_t\) | \(\sigma_t=1-\alpha_t^2\) | \(\alpha_t=\frac{-\varsigma_t+\sqrt{\varsigma_t^2+4}}{2}\) |
| Rectified Flow | \(dx_t = -\frac{1}{2}\beta(t)x_tdt + \sqrt{\beta(t)\left( 1-\exp\left(-\frac{1}{2}\int_0^t\beta(s)ds\right) \right)}dw_t\) | \(\sigma_t=1-\alpha_t\) | \(\alpha_t=\frac{1}{1+\varsigma_t}\) |
VP SDE
DDPMのように\(\alpha_t^2+\sigma_t^2=1\)となるSDEはVP SDE(分散保存型SDE, Variance Preserving SDE)と呼ばれる。
VP SDEは次の式で表される。
\begin{align} dx_t = -\frac{1}{2}\beta(t)x_tdt + \sqrt{\beta(t)}dw_t \\ \end{align}
\(\varsigma_t:=\sigma_t/\alpha_t\)とすると、\(\varsigma_t\)は\(t\)に対して単調増加なので、\(\alpha_t, \sigma_t\)は\(t\)の代わりに\(\varsigma_t\)でパラメーター化することができる。このときの表現は次のようになる。
\begin{align} \begin{cases} \alpha_t &= \frac{1}{\sqrt{1+\varsigma_t^2}} \\ \sigma_t &= \frac{\varsigma_t}{\sqrt{1+\varsigma_t^2}} \\ \end{cases} \end{align}
VE SDE
一方、SMLD(Score matching with Langevin dynamics, スコアモデル)という理論では\(\alpha_t=1\)という条件を考える。こちらはVE SDE(分散発散型SDE, Variance Exploding SDE)と呼ばれる。
\(f(t)=\frac{\alpha_t'}{\alpha_t}=0\)なので、SDEは次の式で表される。
\begin{align} dx_t = g(t)dw_t \\ \end{align}
\(\alpha_t, \sigma_t\)を\(\varsigma_t\)によってパラメーター化すると次のようになる。
\begin{align} \begin{cases} \alpha_t &= 1 \\ \sigma_t &= \varsigma_t \\ \end{cases} \end{align}
sub-VP SDE
sub-VP SDEは、VP SDEと同じ\(\beta(t)\)を用いて次のように定義される。
\begin{align} dx_t = -\frac{1}{2}\beta(t)x_tdt + \sqrt{\beta(t)\left( 1-\exp\left(-2\int_0^t\beta(s)ds\right) \right)}dw_t \end{align}
前述のSDEとα, σとの関係に当てはめると、
\begin{align} \alpha(t) &= \exp\left(\int_0^tf(s)ds\right) \\ &= \exp\left(-\frac{1}{2}\int_0^t\beta(s)ds\right) \\ \end{align}
となり、\(\beta(t)=-2\frac{\alpha'(t)}{\alpha(t)}\)が成り立つので、
\begin{align} \sigma_t^2 &= \alpha_t^2\int_0^t\frac{g(s)^2}{\alpha_s^2}ds \\ &= \alpha_t^2\int_0^t\frac{\beta(s)\left(1-\alpha_s^4\right)}{\alpha_s^2}ds \\ &= \alpha_t^2\int_0^t\frac{-2\frac{\alpha_s'}{\alpha_s}\left(1-\alpha_s^4\right)}{\alpha_s^2}ds \\ &= \alpha_t^2\int_0^t 2\left( -\frac{1}{\alpha_s^3} + \alpha_s \right)\alpha_s'ds \\ &= \alpha_t^2 \left[ \frac{1}{\alpha_s^2} + \alpha_s^2 \right]_0^t \\ &= \alpha_t^2 \left( \frac{1}{\alpha_t^2} + \alpha_t^2 - 1 - 1 \right) \\ &= \alpha_t^4 - 2\alpha_t^2 +1 \\ &= \left(1-\alpha_t^2\right)^2 \\ \end{align}
となって、\(\sigma_t=1-\alpha_t^2\)という関係を得ることができる。
\(\varsigma_t\)を用いて表すと、
\begin{align} \varsigma_t\alpha_t = \sigma_t = 1-\alpha_t^2 \end{align}
となるので、
\begin{align} \begin{cases} \alpha_t &= \frac{-\varsigma_t+\sqrt{\varsigma_t^2+4}}{2} \\ \sigma_t &= \varsigma_t\frac{-\varsigma_t+\sqrt{\varsigma_t^2+4}}{2} \\ \end{cases} \end{align}
Rectified Flow
Rectified Flowという理論では、\(\alpha_t+\sigma_t=1\)という条件を考える。
このとき、
\begin{align} g(t) &= \sqrt{\alpha_t^2\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}} \\ &= \sqrt{\alpha_t^2\frac{d}{dt}\left( \frac{1}{\alpha_t}-1 \right)^2} \\ &= \sqrt{\alpha_t^22\left( \frac{1}{\alpha_t}-1 \right)\left(-\frac{\alpha_t'}{\alpha_t^2}\right)} \\ &= \sqrt{-2f(t)(1-\alpha_t)} \\ \end{align}
なので、SDEは次のように表すことができる。
\begin{align} dx_t = -\frac{1}{2}\beta(t)x_tdt + \sqrt{\beta(t)\left( 1-\exp\left(-\frac{1}{2}\int_0^t\beta(s)ds\right) \right)}dw_t \end{align}
\(\alpha_t, \sigma_t\)を\(\varsigma_t\)によってパラメーター化すると次のようになる。
\begin{align} \begin{cases} \alpha_t &= \frac{1}{1+\varsigma_t} \\ \sigma_t &= \frac{\varsigma_t}{1+\varsigma_t} \\ \end{cases} \end{align}
VP SDEとVE SDEの相互変換
VP SDE(\(\alpha_t^2+\sigma_t^2=1\))とVE SDE(\(\alpha_t=1\))が相互に変換可能であることを示す。
すなわち、VP SDEの条件を前提に導き出された理論は変数変換することでVE SDEにも適用できるし、その逆もまた可能であるということになる。
VP SDEへの変換
(VE SDEを含む)一般の拡散過程に対して、
\begin{align} \begin{cases} \hat{x}_t &:= \frac{x_t}{\sqrt{\alpha_t^2+\sigma_t^2}} \\ \hat{\alpha}_t &:= \frac{\alpha_t}{\sqrt{\alpha_t^2+\sigma_t^2}} \\ \hat{\sigma}_t &:= \frac{\sigma_t}{\sqrt{\alpha_t^2+\sigma_t^2}} \\ \end{cases} \end{align}
とすれば\(\hat{x}_t = \hat{\alpha}_t x_0 + \hat{\sigma}_t \varepsilon\)が成り立ち、この過程はVP SDEとなる。
元のSDEは
\begin{align} dx_t &= f(t)x_tdt + g(t)dw_t \\ &= \frac{\alpha'(t)}{\alpha(t)}x_tdt + \sqrt{\alpha_t^2\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}}dw_t \\ \end{align}
なので、変換後のSDEは以下。
\begin{align} d\hat{x}_t &= -\left(\alpha'_t\alpha_t+\sigma'_t\sigma_t\right)\frac{x_t}{\left(\alpha_t^2+\sigma_t^2\right)^{3/2}}dt + \frac{dx_t}{\sqrt{\alpha_t^2+\sigma_t^2}} \\ &= -\left(\alpha'_t\alpha_t+\sigma'_t\sigma_t\right)\frac{x_t}{\left(\alpha_t^2+\sigma_t^2\right)^{3/2}}dt + \frac{1}{\sqrt{\alpha_t^2+\sigma_t^2}}\left(\frac{\alpha'(t)}{\alpha(t)}x_tdt + \sqrt{\alpha_t^2\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}}dw_t\right) \\ &= -\frac{\alpha'_t\alpha_t+\sigma'_t\sigma_t}{\alpha_t^2+\sigma_t^2}\hat{x}_tdt + \frac{\alpha'_t}{\alpha_t}\hat{x}_tdt + \sqrt{\frac{\alpha_t^2\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}}{\alpha_t^2+\sigma_t^2}}dw_t \\ &= -\frac{\sigma_t\left(\alpha_t\sigma'_t-\sigma_t\alpha'_t\right)}{\alpha_t\left(\alpha_t^2+\sigma_t^2\right)}\hat{x}_tdt + \sqrt{\frac{\alpha_t^2\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}}{\alpha_t^2+\sigma_t^2}}dw_t \\ &= -\frac{\sigma_t\frac{\alpha_t^3}{2\sigma_t}\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}}{\alpha_t\left(\alpha_t^2+\sigma_t^2\right)}\hat{x}_tdt + \sqrt{\frac{\alpha_t^2\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}}{\alpha_t^2+\sigma_t^2}}dw_t \\ &= -\frac{1}{2}\frac{\alpha_t^2\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}}{\alpha_t^2+\sigma_t^2}\hat{x}_tdt + \sqrt{\frac{\alpha_t^2\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}}{\alpha_t^2+\sigma_t^2}}dw_t \\ &= -\frac{1}{2}\frac{d}{dt}\log\left(1 + \frac{\sigma_t^2}{\alpha_t^2}\right)\hat{x}_tdt + \sqrt{\frac{d}{dt}\log\left(1 + \frac{\sigma_t^2}{\alpha_t^2}\right)}dw_t \\ \end{align}
ODEは以下。
\begin{align} d\hat{x}_t &= -\frac{1}{2}\frac{d}{dt}\log\left(1 + \frac{\sigma_t^2}{\alpha_t^2}\right)\left( \hat{x}_t + \nabla_{\hat{x}_t} \log p_t(\hat{x}_t) \right) dt \\ &= -\frac{1}{2}\frac{d}{dt}\log\left(1 + \frac{\sigma_t^2}{\alpha_t^2}\right)\left( \hat{x}_t + \sqrt{\alpha_t^2+\sigma_t^2}\nabla_{x_t} \log p_t(x_t) \right) dt \\ &= -\frac{1}{2}\frac{d}{dt}\log\left(1 + \frac{\sigma_t^2}{\alpha_t^2}\right)\left( \hat{x}_t + \sqrt{1+\frac{\alpha_t^2}{\sigma_t^2}}\sigma_t\nabla_{x_t} \log p_t(x_t) \right) dt \\ \end{align}
VE SDEへの変換
また、(VP SDEを含む)一般の拡散過程に対して、
\begin{align} \begin{cases} \hat{x}_t &:= \frac{x_t}{\alpha_t} \\ \hat{\alpha}_t &:= 1 \\ \hat{\sigma}_t &:= \frac{\sigma_t}{\alpha_t} \\ \end{cases} \end{align}
とすれば\(\hat{x}_t = \hat{\alpha}_t x_0 + \hat{\sigma}_t \varepsilon\)が成り立ち、この過程はVE SDEとなる。
変換後のSDEは以下。
\begin{align} d\hat{x}_t &= -\frac{\alpha'_t}{\alpha_t^2}x_tdt + \frac{dx_t}{\alpha_t} \\ &= -\frac{\alpha'_t}{\alpha_t^2}x_tdt + \frac{1}{\alpha_t}\left(\frac{\alpha_t'}{\alpha_t}x_tdt + \sqrt{\alpha_t^2\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}}dw_t\right) \\ &= \sqrt{\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}}dw_t \\ \end{align}
ODEは以下。
\begin{align} d\hat{x}_t &= -\frac{1}{2}\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}\nabla_{\hat{x}_t} \log p_t(\hat{x}_t) dt \\ &= -\frac{1}{2}\frac{d\hat{\sigma}_t^2}{dt}\nabla_{\hat{x}_t} \log p_t(\hat{x}_t) dt \\ &= -\hat{\sigma}_t'\hat{\sigma}_t\nabla_{\hat{x}_t} \log p_t(\hat{x}_t) dt \\ &= -\hat{\sigma}_t'\hat{\sigma}_t\alpha_t\nabla_{x_t} \log p_t(x_t) dt \\ &= -\hat{\sigma}_t'\sigma_t\nabla_{x_t} \log p_t(x_t) dt \\ &= -\sigma_t\nabla_{x_t} \log p_t(x_t) d\hat{\sigma}_t \\ \end{align}
参考
論文
- [2011.13456] Score-Based Generative Modeling through Stochastic Differential Equations
- [2206.00364] Elucidating the Design Space of Diffusion-Based Generative Models
解説
- Taiji Suzuki's Homepage (鈴木大慈) - 勾配ランジュバン動力学 平均場ランジュバン動力学, pp. 5-14
- 岡野原大輔 - 拡散モデル