DDPMの関連技術
2020年6月にDDPMの論文が公開され、その後様々な関連技術が誕生した。この記事ではそれらのDDPM関連技術を解説する。
関連記事
目次
拡散過程の一般化
関連技術を理解する準備として、DDPMで確認した性質がより一般の拡散過程においても成り立つことを確認する。
離れたタイムステップ間の拡散過程
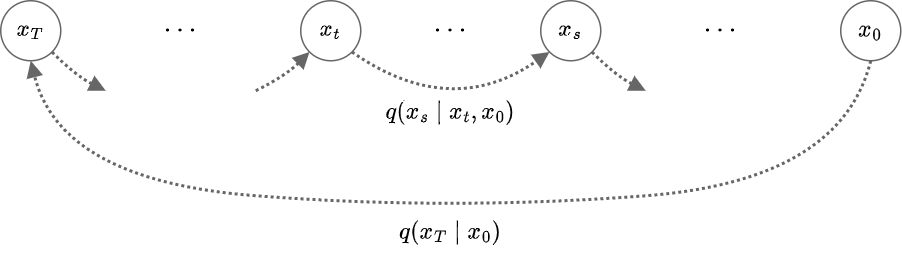
拡散モデルの順過程を以下のように定義する。
\begin{align} q(x_t|x_{t-1}) = p_\mathcal{N}(x_t|k_tx_{t-1},\beta_tI) \end{align}
DDPMでは\(k_t = \sqrt{1-\beta_t}\)としていたが、ここでは平均と分散の係数を独立に与える一般化した拡散過程を考える。
\(s<t\)に対して、
\begin{align} q(x_t|x_s) &= \int q(x_t|x_{t-1}) \cdots q(x_{s+1}|x_s) dx_{s+1:t-1} \\ &= \int q(x_t|x_{t-1}) \cdots q(x_{s+3}|x_{s+2}) \left( \int q(x_{s+2}|x_{s+1})q(x_{s+1}|x_s) dx_{s+1} \right) dx_{s+2:t-1} \\ &= \int q(x_t|x_{t-1}) \cdots q(x_{s+3}|x_{s+2}) \left( \int p_\mathcal{N}(x_{s+2}|k_{s+2}x_{s+1},\beta_{s+2}I) p_\mathcal{N}(x_{s+1}|k_{s+1}x_s,\beta_{s+1}I) dx_{s+1} \right) dx_{s+2:t-1} \\ &= \int q(x_t|x_{t-1}) \cdots q(x_{s+3}|x_{s+2}) \left( \int \frac{1}{k_{s+2}} p_\mathcal{N}\left(\frac{x_{s+2}}{k_{s+2}}\middle|x_{s+1},\frac{\beta_{s+2}}{k_{s+2}^2}I\right) p_\mathcal{N}(x_{s+1}|k_{s+1}x_s,\beta_{s+1}I) dx_{s+1} \right) dx_{s+2:t-1} \\ &= \int q(x_t|x_{t-1}) \cdots q(x_{s+3}|x_{s+2}) \frac{1}{k_{s+2}} p_\mathcal{N}\left(\frac{x_{s+2}}{k_{s+2}}\middle|k_{s+1}x_s,\left(\frac{\beta_{s+2}}{k_{s+2}^2}+\beta_{s+1}\right)I\right) dx_{s+2:t-1} \\ &= \int q(x_t|x_{t-1}) \cdots q(x_{s+3}|x_{s+2}) p_\mathcal{N}\left(x_{s+2}\middle|k_{s+2}k_{s+1}x_s,\left(\beta_{s+2}+k_{s+2}^2\beta_{s+1}\right)I\right) dx_{s+2:t-1} \\ &\quad \vdots \\ &= p_\mathcal{N}\left(x_{s+2}\middle|\left(\prod_{i=s+1}^{t}k_i\right)x_s,\left(\beta_t + k_t^2\beta_{t-1} + k_t^2 k_{t-1}^2\beta_{t-2} + \cdots + \left(\prod_{j=s+2}^t k_j^2\right)\beta_{s+1}\right)I\right) \\ &=: p_\mathcal{N}\left(x_{s+2}\middle|\alpha_{t|s}x_s,\sigma_{t|s}^2I\right) \\ \end{align}
となる。ここで、
\begin{align} \alpha_{t|s} &:= \prod_{i=s+1}^{t}k_i, \\ \sigma_{t|s}^2 &:= \beta_t + k_t^2\beta_{t-1} + k_t^2 k_{t-1}^2\beta_{t-2} + \cdots + \left(\prod_{j=s+2}^t k_j^2\right)\beta_{s+1} \\ &:= \sum_{i=s+1}^t \alpha_{t|i}^2\beta_i \\ \end{align}
特に、
\begin{align} \begin{cases} \alpha_{t} &:= \alpha_{t|0} = \prod_{i=1}^{t}k_i \\ \sigma_{t}^2 &:= \sigma_{t|0}^2 = \sum_{i=1}^t \alpha_{t|i}^2\beta_i \\ \end{cases} \end{align}
とすると、\(\alpha_{t|s}, \sigma_{t|s}^2\)は\(\alpha_t, \sigma_t^2\)を用いて以下のように表すことができる。
\begin{align} \alpha_{t|s} &= \prod_{i=s+1}^{t}k_i \\ &= \frac{\alpha_{t}}{\alpha_{s}}, \\ \sigma_{t|s}^2 &= \sum_{i=s+1}^t \alpha_{t|i}^2\beta_i \\ &= \sum_{i=1}^t \alpha_{t|i}^2\beta_i - \sum_{i=1}^s \alpha_{t|i}^2\beta_i \\ &= \sigma_t^2 - \sum_{i=1}^s \alpha_{t|s}^2\alpha_{s|i}^2\beta_i \\ &= \sigma_t^2 - \alpha_{t|s}^2\sum_{i=1}^s \alpha_{s|i}^2\beta_i \\ &= \sigma_t^2 - \alpha_{t|s}^2\sigma_s^2 \\ \end{align}
Markov拡散過程において
\begin{align} q(x_t|x_0) = p_\mathcal{N}(x_t|\alpha_t x_0, \sigma_t^2 I) \\ \end{align}
となるとき、以下の関係が成り立つ。
\begin{align} q(x_t|x_s) = p_\mathcal{N}(x_t|\alpha_{t|s} x_s, \sigma_{t|s}^2 I) \\ \begin{cases} \alpha_{t|s} = \frac{\alpha_{t}}{\alpha_{s}} \\ \sigma_{t|s}^2 = \sigma_t^2 - \alpha_{t|s}^2\sigma_s^2 \\ \end{cases} \end{align}
ここで、分散\(\sigma_t^2\)と平均の係数\(\alpha_t\)の2乗との比をsignal-to-noise ratio(SNR)と呼ぶ。
\begin{align} SNR(t) = \frac{\alpha_t^2}{\sigma_t^2} \end{align}
離れたタイムステップ間の条件付き確率
DDPMと同じように、今度は\(q(x_s|x_t,x_0)\)を求める。
一般に、次のように2つの正規分布の積は正規分布の定数倍となる。
\begin{align} & p_\mathcal{N}(x|\mu_1,\Sigma_1)p_\mathcal{N}(x|\mu_2,\Sigma_2) \\ \propto &p_\mathcal{N}\left(x\middle|(\Sigma_1+\Sigma_2)^{-1}(\Sigma_2\mu_1+\Sigma_1\mu_2),\Sigma_1\Sigma_2(\Sigma_1+\Sigma_2)^{-1}\right) \\ \end{align}
このことから、
\begin{align} q(x_s|x_t,x_0) &= \frac{q(x_t|x_s,x_0)q(x_s|x_0)}{q(x_t|x_0)} \\ &\propto p_\mathcal{N}\left( x_t \middle| \alpha_{t|s}x_s, \sigma_{t|s}^2I \right) p_\mathcal{N}\left( x_s \middle| \alpha_sx_0, \sigma_s^2I \right) \\ &= p_\mathcal{N}\left( x_s \middle| \frac{x_t}{\alpha_{t|s}}, \frac{\sigma_{t|s}^2}{\alpha_{t|s}^2}I \right) p_\mathcal{N}\left( x_s \middle| \alpha_sx_0, \sigma_s^2I \right) \\ &\propto p_\mathcal{N}\left( x_s \middle| \frac{1}{\frac{\sigma_{t|s}^2}{\alpha_{t|s}^2}+\sigma_s^2}\left( \sigma_s^2\frac{x_t}{\alpha_{t|s}} + \frac{\sigma_{t|s}^2}{\alpha_{t|s}^2}\alpha_sx_0 \right), \frac{\frac{\sigma_{t|s}^2}{\alpha_{t|s}^2}\sigma_s^2}{\frac{\sigma_{t|s}^2}{\alpha_{t|s}^2}+\sigma_s^2}I \right) \\ &= p_\mathcal{N}\left( x_s \middle| \frac{1}{\sigma_t^2}\left( \alpha_{t|s}\sigma_s^2x_t + \alpha_s\sigma_{t|s}^2x_0 \right), \frac{\sigma_{t|s}^2\sigma_s^2}{\sigma_t^2}I \right) \\ &= p_\mathcal{N}\left( x_s \middle| \tilde{\mu}_{s|t}(x_t,x_0), \tilde{\beta}_{s|t}I \right) \\ \end{align}
となる。ここで、
\begin{align} \begin{cases} \tilde{\mu}_{s|t}(x_t,x_0) &:= \frac{1}{\sigma_t^2}\left( \alpha_{t|s}\sigma_s^2x_t + \alpha_s\sigma_{t|s}^2x_0 \right) \\ \tilde{\beta}_{s|t} &:= \frac{\sigma_{t|s}^2\sigma_s^2}{\sigma_t^2} \\ \end{cases} \end{align}
\(\tilde{\mu}_{s|t}(x_t,x_0)\)は\(\tilde{\beta}_{s|t}\)を用いて以下のように表すこともできる。(ただし、\(\varepsilon_t(x_t,x_0):=\frac{x_t-\alpha_tx_0}{\sigma_t}\))
\begin{align} \tilde{\mu}_{s|t}(x_t,x_0) &:= \frac{1}{\sigma_t^2}\left( \alpha_{t|s}\sigma_s^2x_t + \alpha_s\sigma_{t|s}^2x_0 \right) \\ &= \frac{1}{\sigma_t^2}\left( \alpha_{t|s}\sigma_s^2x_t + \alpha_s(\sigma_t^2-\alpha_{t|s}^2\sigma_s^2)x_0 \right) \\ &= \alpha_sx_0 + \frac{\sigma_s^2\alpha_{t|s}}{\sigma_t^2}\left( x_t - \alpha_s\alpha_{t|s}x_0 \right) \\ &= \alpha_sx_0 + \sqrt{\frac{\sigma_s^4\alpha_{t|s}^2}{\sigma_t^4}}\left( x_t - \alpha_tx_0 \right) \\ &= \alpha_sx_0 + \sqrt{\frac{\sigma_s^2(\sigma_t^2-\sigma_{t|s}^2)}{\sigma_t^4}}\left( x_t - \alpha_tx_0 \right) \\ &= \alpha_sx_0 + \sqrt{\sigma_s^2 - \frac{\sigma_s^2\sigma_{t|s}^2}{\sigma_t^2}}\frac{ x_t - \alpha_tx_0 }{\sigma_t} \\ &= \alpha_sx_0 + \sqrt{\sigma_s^2 - \tilde{\beta}_{s|t}}\varepsilon_t(x_t,x_0) \\ \end{align}
また、\(x_t\)と\(\varepsilon_t(x_t,x_0)\)で次のように表すこともできる。
\begin{align} \tilde{\mu}_{s|t}(x_t,x_0) &= \frac{1}{\sigma_t^2}\left( \alpha_{t|s}\sigma_s^2x_t + \alpha_s\sigma_{t|s}^2x_0 \right) \\ &= \frac{1}{\sigma_t^2}\left( \alpha_{t|s}\sigma_s^2x_t + \alpha_s\sigma_{t|s}^2\frac{x_t-\sigma_t\varepsilon_t(x_t,x_0)}{\alpha_t} \right) \\ &= \frac{1}{\sigma_t^2}\left( \frac{\alpha_t}{\alpha_s}\sigma_s^2x_t + \frac{\alpha_s}{\alpha_t}\sigma_{t|s}^2x_t - \frac{\alpha_s}{\alpha_t}\sigma_{t|s}^2\sigma_t\varepsilon_t(x_t,x_0) \right) \\ &= \frac{1}{\sigma_t^2}\left( \frac{\alpha_t}{\alpha_s}\sigma_s^2x_t + \frac{\alpha_s}{\alpha_t}\left(\sigma_t^2-\frac{\alpha_t^2}{\alpha_s^2}\sigma_s^2\right)x_t - \frac{\alpha_s}{\alpha_t}\sigma_{t|s}^2\sigma_t\varepsilon_t(x_t,x_0) \right) \\ &= \frac{\alpha_s}{\alpha_t}x_t - \frac{\alpha_s}{\alpha_t}\frac{\sigma_{t|s}^2}{\sigma_t^2}\sigma_t\varepsilon_t(x_t,x_0) \\ &= \frac{\alpha_s}{\alpha_t}x_t - \frac{\alpha_s}{\alpha_t}\frac{\tilde{\beta}_{s|t}}{\sigma_s^2}\sigma_t\varepsilon_t(x_t,x_0) \\ &= \frac{1}{\alpha_{t|s}}\left( x_t - \frac{\tilde{\beta}_{s|t}}{\sigma_s^2}\sigma_t\varepsilon_t(x_t,x_0) \right) \\ \end{align}
特にDDPMの場合、\(\sigma_t^2=1-\alpha_t^2\)なので\(\tilde{\mu}_{s|t}(x_t,x_0), \tilde{\beta}_{s|t}\)は次のようになる。
\begin{align} \tilde{\mu}_{s|t}(x_t,x_0) &= \alpha_sx_0 + \sqrt{\sigma_s^2 - \tilde{\beta}_{s|t}}\frac{ x_t - \alpha_tx_0 }{\sigma_t} \\ &= \alpha_sx_0 + \sqrt{1 - \alpha_s^2 - \tilde{\beta}_{s|t}}\frac{ x_t - \alpha_tx_0 }{\sqrt{1-\alpha_t^2}} \\ \end{align}
\begin{align} \tilde{\beta}_{s|t} &:= \frac{\sigma_s^2}{\sigma_t^2}\sigma_{t|s}^2 \\ &= \frac{\sigma_s^2}{\sigma_t^2}(\sigma_t^2 - \alpha_{t|s}^2\sigma_s^2) \\ &= \frac{1-\alpha_s^2}{1-\alpha_t^2}\left(1-\alpha_t^2 - \frac{\alpha_t^2}{\alpha_s^2}(1-\alpha_s^2)\right) \\ &= \frac{1-\alpha_s^2}{1-\alpha_t^2}\left(1-\frac{\alpha_t^2}{\alpha_s^2}\right) \\ \end{align}
\(s<t\)に対して以下が成り立つ。
\begin{align} q(x_s|x_t,x_0) = p_\mathcal{N}\left( x_s \middle| \tilde{\mu}_{s|t}(x_t,x_0), \tilde{\beta}_{s|t}I \right) \\ \begin{cases} \tilde{\mu}_{s|t}(x_t,x_0) &:= \frac{1}{\sigma_t^2}\left( \alpha_{t|s}\sigma_s^2x_t + \alpha_s\sigma_{t|s}^2x_0 \right) \\ &= \alpha_sx_0 + \sqrt{\sigma_s^2 - \tilde{\beta}_{s|t}}\varepsilon_t(x_t,x_0) \\ &= \frac{1}{\alpha_{t|s}}\left( x_t - \frac{\tilde{\beta}_{s|t}}{\sigma_s^2}\sigma_t\varepsilon_t(x_t,x_0) \right) \\ \tilde{\beta}_{s|t} &:= \frac{\sigma_{t|s}^2\sigma_s^2}{\sigma_t^2} \\ \end{cases} \end{align}
特にDDPM (\(\sigma_t^2=1-\alpha_t^2\))の場合、
\begin{align} \begin{cases} \tilde{\mu}_{s|t}(x_t,x_0) &= \alpha_sx_0 + \sqrt{1 - \alpha_s^2 - \tilde{\beta}_{s|t}}\varepsilon_t(x_t,x_0) \\ \tilde{\beta}_{s|t} &= \frac{1-\alpha_s^2}{1-\alpha_t^2}\left(1-\frac{\alpha_t^2}{\alpha_s^2}\right) \\ \end{cases} \end{align}
離れたタイムステップ間の損失項
時刻\(t\)の画像の入力に対して、時刻\(s\)の画像を出力するモデル\(p_\theta(x_s|x_t) = p_\mathcal{N}(x_s|\mu_\theta(x_t,t),\tilde{\beta}_{s|t}I)\)を学習するとき、DDPMで考えた損失項は以下のようになる。
\begin{align} D_{KL}\left(q(x_s|x_t,x_0)\middle\|p_\theta(x_s|x_t)\right) &= \frac{1}{2\tilde{\beta}_{s|t}}\| \tilde{\mu}_{s|t}(x_t,x_0) - \mu_\theta(x_t,t) \|^2 \\ \end{align}
\(x_s\)の平均\(\mu_\theta(x_t,t)\)ではなく、\(x_0\)を予測するモデル\(x_{0,\theta}(x_t,t)\)の場合:
\begin{align} D_{KL}\left(q(x_s|x_t,x_0)\middle\|p_\theta(x_s|x_t)\right) &= \frac{1}{2\tilde{\beta}_{s|t}}\| \tilde{\mu}_{s|t}(x_t,x_0) - \mu_\theta(x_t,t) \|^2 \\ &= \frac{1}{2\tilde{\beta}_{s|t}}\left\| \frac{\alpha_s\sigma_{t|s}^2}{\sigma_t^2}x_0 - \frac{\alpha_s\sigma_{t|s}^2}{\sigma_t^2}x_{0,\theta}(x_t,t) \right\|^2 \\ &= \frac{1}{2}\frac{\sigma_t^2}{\sigma_{t|s}^2\sigma_s^2}\frac{\alpha_s^2\sigma_{t|s}^4}{\sigma_t^4}\| x_0 - x_{0,\theta}(x_t,t) \|^2 \\ &= \frac{1}{2}\frac{\alpha_s^2\sigma_{t|s}^2}{\sigma_s^2\sigma_t^2}\| x_0 - x_{0,\theta}(x_t,t) \|^2 \\ &= \frac{1}{2}\frac{\alpha_s^2(\sigma_t^2 - \alpha_{t|s}^2\sigma_s^2)}{\sigma_s^2\sigma_t^2}\| x_0 - x_{0,\theta}(x_t,t) \|^2 \\ &= \frac{1}{2}\left(\frac{\alpha_s^2}{\sigma_s^2}-\frac{\alpha_t^2}{\sigma_t^2}\right)\| x_0 - x_{0,\theta}(x_t,t) \|^2 \\ &= \frac{1}{2}\left(SNR(s)-SNR(t)\right)\| x_0 - x_{0,\theta}(x_t,t) \|^2 \\ \end{align}
ノイズ\(\varepsilon\)を予測するモデル\(\varepsilon_\theta(x_t,t)\)の場合:
\begin{align} D_{KL}\left(q(x_s|x_t,x_0)\middle\|p_\theta(x_s|x_t)\right) &= \frac{1}{2}\left(SNR(s)-SNR(t)\right)\| x_0 - x_{0,\theta}(x_t,t) \|^2 \\ &= \frac{1}{2}\left(SNR(s)-SNR(t)\right)\left\| \frac{x_t-\sigma_t\varepsilon}{\alpha_t} - \frac{x_t-\sigma_t\varepsilon_\theta(x_t,t)}{\alpha_t} \right\|^2 \\ &= \frac{1}{2}\left(SNR(s)-SNR(t)\right)\frac{\sigma_t^2}{\alpha_t^2}\| \varepsilon - \varepsilon_\theta(x_t,t) \|^2 \\ &= \frac{1}{2}\left(\frac{SNR(s)}{SNR(t)}-1\right)\| \varepsilon - \varepsilon_\theta(x_t,t) \|^2 \\ \end{align}
\begin{align} D_{KL}\left(q(x_s|x_t,x_0)\middle\|p_\theta(x_s|x_t)\right) &= \frac{1}{2\tilde{\beta}_{s|t}}\| \tilde{\mu}_{s|t}(x_t,x_0) - \mu_\theta(x_t,t) \|^2 \\ &= \frac{1}{2}\left(SNR(s)-SNR(t)\right)\| x_0 - x_{0,\theta}(x_t,t) \|^2 \\ &= \frac{1}{2}\left(\frac{SNR(s)}{SNR(t)}-1\right)\| \varepsilon - \varepsilon_\theta(x_t,t) \|^2 \\ \end{align}
DDIM
DDIM(Denoising Diffusion Implicit Models)は2020年10月に提案されたDDPMの新しい画像生成アルゴリズム。
DDPMでは\(T=1000\)ステップのモデル実行が必要だったが、DDIMの方法では20~100ステップ程度でも高品質の画像を生成できることが示された。
DDIMでは拡散過程のMarkov性を撤廃し、以下の分布を前提として定めて議論を進める。
\(\{0,1,2,\cdots,T\}\)の部分列\(\tau=\{\tau_1, \tau_2, \cdots , \tau_I\}\)を任意に取る。
ただし、\(\tau_0=0, \tau_I=T\)とする。
\(\tau\)に含まれる任意の隣接する2つの要素\((s,t)=(\tau_{i-1},\tau_i)\)に対して、次のように定義される(非Markov)確率過程を考える。
\begin{align} \begin{cases} q (x_T|x_0) &:= p_\mathcal{N}(x_T|\alpha_Tx_0,(1-\alpha_T^2)I) \\ q (x_s|x_t,x_0) &:= p_\mathcal{N}\left(x_s\middle|\alpha_sx_0+\sqrt{\sigma_s^2-s_t^2}\frac{x_t-\alpha_tx_0}{\sigma_t},s_t^2I\right) \\ \end{cases} \end{align}
この定義は上で求めた条件付き確率の結果に由来している。
特に、\(\alpha_t^2+\sigma_t^2=1\)とし、\(s_t^2 = \tilde{\beta}_{s|t} = \frac{1-\alpha_s^2}{1-\alpha_t^2}\left(1-\frac{\alpha_t^2}{\alpha_s^2}\right)\)とすればDDPMと一致することがわかる。
DDPMとの比較
\(q (x_t|x_0)\)
この先、特に断りがない限り\(t\in\tau\)の一つ前の要素を\(s\)と表記する。
\(r_t := \frac{\sqrt{\sigma_s^2-s_t^2}}{\sigma_t}\)と置くと、
\begin{align} q (x_s|x_t,x_0) &= p_\mathcal{N}\left(x_s\middle|\alpha_sx_0+r_t(x_t-\alpha_tx_0),s_t^2I\right) \\ &= p_\mathcal{N}\left(x_s\middle|r_tx_t + (\alpha_s - \alpha_tr_t)x_0,s_t^2I\right) \\ \end{align}
と表すことができる。
\begin{align} q (x_{\tau_{I-1}}|x_0) &= \int q (x_T|x_0)q (x_{\tau_{I-1}}|x_T,x_0) dx_T \\ &= \int p_\mathcal{N}(x_T|\alpha_Tx_0,\sigma_T^2I) p_\mathcal{N}\left(x_{\tau_{I-1}}\middle|r_Tx_T + (\alpha_{\tau_{I-1}} - \alpha_Tr_T)x_0,s_T^2I\right) dx_T \\ &= \int p_\mathcal{N}(x_T|\alpha_Tx_0,\sigma_T^2I) p_\mathcal{N}\left(\frac{x_{\tau_{I-1}} - (\alpha_{\tau_{I-1}} - \alpha_Tr_T)x_0}{r_T}\middle|x_T,\frac{s_T^2}{r_T^2}I\right) dx_T \\ &= p_\mathcal{N}\left(\frac{x_{\tau_{I-1}} - (\alpha_{\tau_{I-1}} - \alpha_Tr_T)x_0}{r_T}\middle|\alpha_Tx_0,\left(\frac{s_T^2}{r_T^2} + \sigma_T^2\right)I\right) \\ &= p_\mathcal{N}\left(x_{\tau_{I-1}}\middle|r_T\alpha_Tx_0 + (\alpha_{\tau_{I-1}} - \alpha_Tr_T)x_0,\left(s_T^2 + r_T^2\sigma_T^2\right)I\right) \\ &= p_\mathcal{N}\left(x_{\tau_{I-1}}\middle|\alpha_{\tau_{I-1}}x_0,\left(s_T^2 + \frac{\sigma_{\tau_{I-1}}^2-s_T^2}{\sigma_T^2}\sigma_T^2\right)I\right) \\ &= p_\mathcal{N}\left(x_{\tau_{I-1}}\middle|\alpha_{\tau_{I-1}}x_0,\sigma_{\tau_{I-1}}^2I\right) \\ \end{align}
となるので、帰納的に全ての\(t\in\tau\)に対して、
\begin{align} q (x_t|x_0) = p_\mathcal{N}\left(x_t\middle|\alpha_tx_0,\sigma_t^2I\right) \\ \end{align}
となり、\(q (x_t|x_0)\)がDDPMと一致することがわかる。
\(q (x_t|x_s,x_0)\)
また、\(q (x_t|x_s,x_0)\)については、
\begin{align} q (x_t|x_s,x_0) &= \frac{q(x_s|x_t,x_0)q(x_t|x_0)}{q(x_s|x_0)} \\ &\propto p_\mathcal{N}\left(x_s\middle|r_tx_t + (\alpha_s - \alpha_tr_t)x_0,s_t^2I\right) p_\mathcal{N}\left(x_t\middle|\alpha_tx_0,\sigma_t^2I\right) \\ &= p_\mathcal{N}\left(x_t\middle|\frac{1}{r_t}(x_s - (\alpha_s - \alpha_tr_t)x_0),\frac{s_t^2}{r_t^2}I\right) p_\mathcal{N}\left(x_t\middle|\alpha_tx_0,\sigma_t^2I\right) \\ &\propto p_\mathcal{N}\left(x_t\middle|\frac{\frac{1}{r_t}(x_s - (\alpha_s - \alpha_tr_t)x_0)\sigma_t^2 + \alpha_tx_0\frac{s_t^2}{r_t^2}}{\frac{s_t^2}{r_t^2} + \sigma_t^2},\frac{\frac{s_t^2}{r_t^2}\sigma_t^2}{\frac{s_t^2}{r_t^2} + \sigma_t^2}I\right) \\ \end{align}
となる。ここで、
\begin{align} \frac{s_t^2}{r_t^2} + \sigma_t^2 &= \frac{s_t^2 + r_t^2\sigma_t^2}{r_t^2} \\ &= \frac{s_t^2 + \sigma_s^2-s_t^2}{r_t^2} \\ &= \frac{\sigma_s^2}{r_t^2} \\ \end{align}
なので、
\begin{align} \frac{\frac{s_t^2}{r_t^2}\sigma_t^2}{\frac{s_t^2}{r_t^2} + \sigma_t^2} = s_t^2\frac{\sigma_t^2}{\sigma_s^2} \end{align}
また、
\begin{align} &\quad \frac{\frac{1}{r_t}(x_s - (\alpha_s - \alpha_tr_t)x_0)\sigma_t^2 + \alpha_tx_0\frac{s_t^2}{r_t^2}}{\frac{s_t^2}{r_t^2} + \sigma_t^2} \\ &= \frac{r_t(x_s - (\alpha_s - \alpha_tr_t)x_0)\sigma_t^2 + \alpha_tx_0s_t^2}{\sigma_s^2} \\ &= r_t\frac{\sigma_t^2}{\sigma_s^2}x_s + \frac{1}{\sigma_s^2}\left( -r_t(\alpha_s - \alpha_tr_t)\sigma_t^2 + \alpha_ts_t^2 \right)x_0 \\ &= r_t\frac{\sigma_t^2}{\sigma_s^2}x_s + \frac{1}{\sigma_s^2}\left( -r_t\alpha_s\sigma_t^2 + \alpha_t\left(r_t^2\sigma_t^2 + s_t^2\right) \right)x_0 \\ &= r_t\frac{\sigma_t^2}{\sigma_s^2}x_s + \frac{1}{\sigma_s^2}\left( -r_t\alpha_s\sigma_t^2 + \alpha_t\sigma_s^2 \right)x_0 \\ &= r_t\frac{\sigma_t^2}{\sigma_s^2}x_s + \left( \alpha_t - \alpha_sr_t\frac{\sigma_t^2}{\sigma_s^2} \right)x_0 \\ \end{align}
したがって、これらの結果を合わせると\(q (x_t|x_s,x_0)\)は次のようになる。
\begin{align} q (x_t|x_s,x_0) &= p_\mathcal{N}\left(x_t\middle|r_t\frac{\sigma_t^2}{\sigma_s^2}x_s + \left( \alpha_t - \alpha_sr_t\frac{\sigma_t^2}{\sigma_s^2} \right)x_0,s_t^2\frac{\sigma_t^2}{\sigma_s^2}I\right) \\ \end{align}
\(q (x_t|x_s,x_0)\)が\(x_0\)に依存しない必要十分条件は、
\begin{align} & 0 = \alpha_t - \alpha_sr_t\frac{\sigma_t^2}{\sigma_s^2} \\ & \Leftrightarrow \frac{\alpha_t^2}{\alpha_s^2}\frac{\sigma_s^4}{\sigma_t^4} = r_t^2 = \frac{\sigma_s^2-s_t^2}{\sigma_t^2} \\ \end{align}
したがって、
\begin{align} s_t^2 &= \sigma_s^2 - \frac{\alpha_t^2}{\alpha_s^2}\frac{\sigma_s^4}{\sigma_t^2} \\ &= \frac{\sigma_s^2}{\sigma_t^2}\left(\sigma_t^2 - \frac{\alpha_t^2}{\alpha_s^2}\sigma_s^2 \right) \\ &= \frac{\sigma_s^2}{\sigma_t^2}\sigma_{t|s}^2 \\ &= \tilde{\beta}_{s|t} \\ \end{align}
となり、DDPMの条件と一致する。つまり、DDIMがMarkov過程になるのはDDPMと一致する場合だけということになる。
損失関数の導出
DDPMと同様に損失関数を計算する。
\begin{align} Loss &= E_{q(x_{1:T}|x_0)q(x_0)}\left( \log\frac{q(x_T|x_0)}{p(x_T)} \right) + \sum_{t\in\tau} E_{q(x_{1:T}|x_0)q(x_0)}\left( \log\frac{q(x_s|x_t,x_0)}{p_\theta(x_s|x_t)} \right) \\ &= I E_{x_0,t,x_t}\left( D_{KL}\left( q(x_s|x_t,x_0) \middle\| p_\theta(x_s|x_t) \right) \right) + C \\ &= \frac{I}{2} E_{x_0,t,x_t}\left( \frac{\left(\alpha_s-\alpha_tr_t\right)^2}{s_t^2} \|x_0 - x_{0,\theta}(x_t,t)\|^2 \right) + C \\ &= \frac{I}{2} E_{x_0,t,\varepsilon}\left( \frac{\left(\alpha_s-\alpha_tr_t\right)^2}{s_t^2} \frac{\sigma_t^2}{\alpha_t^2} \|\varepsilon - \varepsilon_\theta(x_t,t)\|^2 \right) + C \\ \end{align}
しかし、DDPMの実験でも確かめられたように、\(\|\varepsilon - \varepsilon_\theta(x_t,t)\|^2\)の係数は1に簡略化しても学習の品質に悪影響がないことがわかっている。したがって、結局DDPMと同様に簡素化した損失関数で学習することができる。
\begin{align} Loss_{simple} &= E_{x_0,t,x_t}\left( \|\varepsilon - \varepsilon_\theta(x_t,t)\|^2 \right) \\ \end{align}
この損失関数はDDPMで用いるものと全く同じなので、DDPMで学習した結果をそのまま流用することでき、DDIMのためにモデルを改めて学習する必要はない。
生成過程
生成過程は最初に定義した確率分布に従って実行される。
\begin{align} q (x_s|x_t,x_0) &:= p_\mathcal{N}\left(x_s\middle|\alpha_sx_0+\sqrt{\sigma_s^2-s_t^2}\frac{x_t-\alpha_tx_0}{\sigma_t},s_t^2I\right) \\ \end{align}
\(n\sim\mathcal(0,I)\)に対して、\(x_s\)は次のように得られる。
\begin{align} x_s &= \alpha_sx_{0,\theta}(x_t,t)+\sqrt{\sigma_s^2-s_t^2}\frac{x_t-\alpha_tx_{0,\theta}(x_t,t)}{\sigma_t} + s_tn \\ &= \frac{\alpha_s}{\alpha_t}\left(x_t-\sigma_t\varepsilon_{\theta}(x_t,t)\right)+\sqrt{\sigma_s^2-s_t^2}\varepsilon_{\theta}(x_t,t) + s_tn \\ \end{align}
ここで、DDIMでは\(\alpha_t^2+\sigma_t=1\)とし、\(s_t\)を次のように定める。
\begin{align} s_t := \eta \sqrt{\tilde{\beta}_{s|t}} = \eta \sqrt{ \frac{1-\alpha_s^2}{1-\alpha_t^2}\left(1-\frac{\alpha_t^2}{\alpha_s^2}\right) } \end{align}
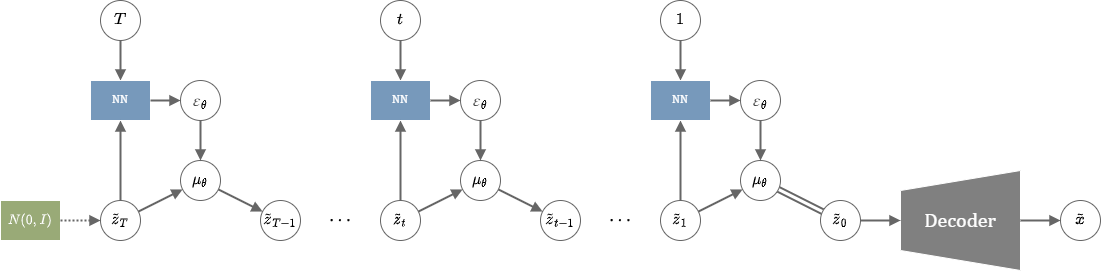
\(\tau=\{\tau_0, \tau_1, \tau_2, \cdots , \tau_I\}\)を\(\{0,1,2,\cdots,T\}\)の部分列とする。
ただし、\(\tau_I=T, \tau_0=0\)。
- \(x_{\tau_I}=x_T\)を\(\mathcal{N}(0,I)\)からサンプル。
- 以下の手順を\((t,s)=(\tau_I,\tau_{I-1}),(\tau_{I-1},\tau_{I-2}),\cdots,(\tau_2,\tau_1),(\tau_1,\tau_0)\)に対して繰り返し行う。
- \(x_t, t\)をニューラルネットワークに入力し、出力\(\varepsilon_\theta\)を得る。
- \(n\sim\mathcal{N}(0,I)\)を取る。
- \(x_s := \frac{\alpha_s}{\alpha_t}(x_t-\sqrt{1-\alpha_t^2}\varepsilon_{\theta})+\sqrt{1-\alpha_s^2-s_t^2}\varepsilon_{\theta} + s_tn\)を計算。
- \(x_0 = x_{\tau_0}\)を画像として出力。
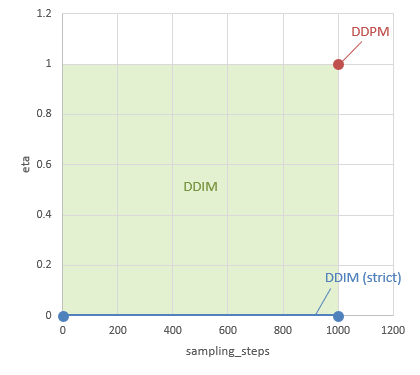
\(\eta\in[0,1]\)の自由度があるが、論文では特に\(\eta = 0\)の場合をDDIMと呼んでいる。
\(\eta=1\)で\(\tau=\{0,1,\cdots,T\}\)の場合はDDPMと一致する。
CFG
Classifier Guidance
Classifier Guidanceは、学習済みの拡散生成モデルに対する画像サンプリングの技術。画像の入力\(x\)に対してクラス\(c\)を出力する分類モデル\(p_\theta(c|x)\)を利用することで、利用者が指定したクラスに当てはまる画像を拡散モデルでより多く出力させることができるようになる。
2021年5月にOpenAIの技術者が発表した論文「Diffusion Models Beat GANs on Image Synthesis」に登場した。
\(q(x_t|x_0) = p_\mathcal{N}(x_t|\alpha_t x_0, \sigma_t^2 I)\)であるとし、拡散過程において\(x_t\)が現れる確率\(q(x_t)=\int q(x_t|x_0)p(x_0) dx_0\)の尤度の勾配を計算する。
\begin{align} s(x_t,t) &:= \nabla_{x_t} \log q(x_t) \\ &= \frac{1}{q(x_t)} \nabla_{x_t} q(x_t) \\ &= \frac{1}{q(x_t)} \int \left( \nabla_{x_t} q(x_t|x_0) \right) p(x_0) dx_0 \\ &= \frac{1}{q(x_t)} \int \nabla_{x_t}\left( -\frac{\|x_t-\alpha_t x_0\|^2}{2\sigma_t^2} \right) q(x_t|x_0)p(x_0) dx_0 \\ &= -\frac{1}{q(x_t)} \int \frac{x_t-\alpha_t x_0}{\sigma_t^2} q(x_t|x_0)p(x_0) dx_0 \\ &= -\int \frac{x_t-\alpha_t x_0}{\sigma_t^2} \frac{q(x_t|x_0)p(x_0)}{q(x_t)} dx_0 \\ &= -\int \frac{x_t-\alpha_t x_0}{\sigma_t^2} q(x_0|x_t) dx_0 \\ &= -\frac{\mathbb{E}_{x_0|x_t}\left(\frac{x_t-\alpha_t x_0}{\sigma_t}\right)}{\sigma_t} \\ \end{align}
ここで、\(\varepsilon\sim \mathcal{N}(0,I)\)に対して\(x_t=\alpha_t x_0+\sigma_t\varepsilon\)となることから、\(\frac{x_t-\alpha_t x_0}{\sigma_t}\)はノイズ\(\varepsilon\)を表す値となる。十分学習されたモデルでは\(\varepsilon_\theta(x_t,t)\sim\mathbb{E}_{x_0|x_t}\left(\frac{x_t-\alpha_t x_0}{\sigma_t}\right)\)となる。
したがって、対数尤度の勾配とノイズの期待値には次のように一定の関係があることがわかる。
\begin{align} s(x_t,t) &= \nabla_{x_t} \log q(x_t) \\ &= -\frac{\mathbb{E}_{x_0|x_t}\left(\frac{x_t-\alpha_t x_0}{\sigma_t}\right)}{\sigma_t} \\ &\sim -\frac{\varepsilon_\theta(x_t,t)}{\sigma_t} \\ \end{align}
2019年7月にSongらが発表したLangevin動力学に基づくスコアベースモデルでは、ベクトル場\(s(x_t,t)\)をスコアと呼び、スコアに沿って\(x_t\)の更新を繰り返すことによって尤度の高い\(x_0\)を生成するサンプリング手法が研究されている。Classifier GuidanceやCFGを理解するためにスコアベースモデルの全てを知る必要はないので、ここではスコアベースモデルを詳細には解説しない。
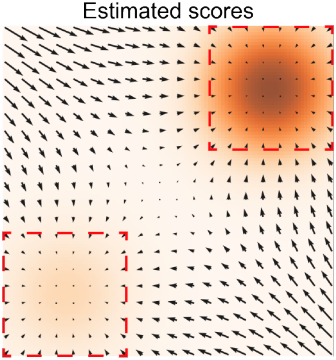
スコアベースモデルの概念図。予測されたスコアに沿って\(x_0\)を探索する。
既存のモデル\(q(x)\)に対して、入力画像以外の条件値\(c\)が与えられた場合の条件付き確率\(q(x|c)\)を考えると、スコアは以下のように計算される。
\begin{align} s(x_t,t,c) &:= \nabla_{x_t} \log q(x_t|c) \\ &= \nabla_{x_t} \log \frac{q(x_t)q(c|x_t)}{q(c)} \\ &= \nabla_{x_t} \log q(x_t) + \nabla_{x_t} \log q(c|x_t) \\ &\sim - \frac{\varepsilon_\theta(x_t,t)}{\sigma_t} + \nabla_{x_t} \log q(c|x_t) \\ &= - \frac{\varepsilon_\theta(x_t,t) - \sigma_t\nabla_{x_t} \log q(c|x_t)}{\sigma_t} \\ \end{align}
ここで、\(\nabla_{x_t} \log q(c|x_t)\)は学習済みの分類モデル\(p_\theta(c|x)\)を利用して計算することができる。分類モデルが勾配降下法によって学習される一般的なニューラルネットワークで実装されている場合、学習のために微分を計算する仕組みが備わっているはずなので、その仕組みを利用して微分を計算して利用すれば良い。
\(\varepsilon_\theta\)を次のように補正し、\(\varepsilon_\theta(x_t,t)\)の代わりに\(\hat{\varepsilon}_\theta(x_t,t,c)\)を用いて生成過程を実行することで、条件値\(c\)に合致する画像を生成できるようになる。
\begin{align} \hat{\varepsilon}_\theta(x_t,t,c) := \varepsilon_\theta(x_t,t) - w\sigma_t\nabla_{x_t} \log p_\theta(c|x_t) \end{align}
\(w\)は分類モデルの効果を強調するための係数。\(w>1\)によって勾配を強める必要があることが実験からわかっている。
CFG
CFG(Classifier-Free Guidance)は、分類モデル\(p_\theta(c|x)\)の代わりに条件付き生成モデル\(p_\theta(x|c)\)(つまり拡散モデルそのもの)を用いることで、Classifier Guidanceと同様の効果を得るための技術。
DDPMの著者であるGoogleのHo氏らが2021年12月に論文を公開した。
学習済みの分類モデル\(p_\theta(c|x)\)が存在せず、生成モデルが条件値\(c\)(Stable Diffusionのpromptに相当)を受け取ることができるモデル\(p_\theta(x|c)\)である場合、補正されたスコアは次のように計算することができる。
\begin{align} \hat{\varepsilon}_\theta(x_t,t,c) &:= \varepsilon_\theta(x_t,t) - w\sigma_t\nabla_{x_t} \log p_\theta(c|x_t) \\ &\sim \varepsilon_\theta(x_t,t) - w\sigma_t\nabla_{x_t} \log q(c|x_t) \\ &= \varepsilon_\theta(x_t,t) - w\sigma_t\nabla_{x_t} \log \frac{q(x_t|c)q(c)}{q(x_t)} \\ &= \varepsilon_\theta(x_t,t) - w\left( \sigma_t\nabla_{x_t} \log q(x_t|c) - \sigma_t\nabla_{x_t} \log q(x_t) \right) \\ &\sim \varepsilon_\theta(x_t,t) + w\left( \varepsilon_\theta(x_t,t,c) - \varepsilon_\theta(x_t,t) \right) \\ \end{align}
ここで、\(\varepsilon_\theta(x_t,t,c)\)と\(\varepsilon_\theta(x_t,t)\)という2つのモデルが必要になるが、実装の上では\(\varepsilon_\theta(x_t,t)=\varepsilon_\theta(x_t,t,null)\)とすることで、どちらも共通の\(\varepsilon_\theta(x_t,t,c)\)だけで表現できる。
共通のモデル\(\varepsilon_\theta(x_t,t,c)\)は、条件値\(c\)を与える場合と与えない場合の両方を混合した学習データによって学習すれば良い。
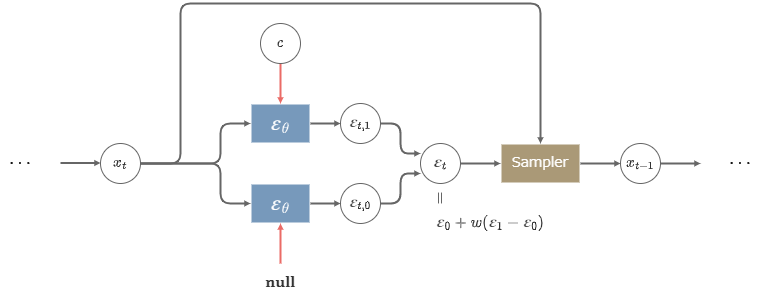
CFGを用いた生成
係数\(w\)はCFG Scaleと呼ばれる。(文脈によっては\(w-1\)をCFG Scaleと呼ぶこともあるので注意)
CFG Scaleが大きいほど、画像の多様性が失われる代わりに、指定した\(c\)という条件に忠実な画像が出力されるようになる。
Classifier GuidanceやCFGの効果は次のように可視化して捉えることができる。

Classifier GuidanceやCFGの効果を可視化した例
この例では、3つのクラスのいずれかに従って2次元空間上に点が生成される。左端の図はcfg_scale=1にあたる出力例であり、右に進むほどcfg_scaleが強くなっていく。
cfg_scale=1の場合は境界が曖昧であり、指定したクラスとは異なるクラスに近い点が生成される可能性があることがわかる。
一方、cfg_scale>1の場合は\(w\)が大きくなるほどクラス間の隔たりが大きくなり、異なるクラスの点を生成することはなくなる。しかし、その一方で生成される点の領域は狭くなり、生成物の多様性が損なわれることがわかる。
beta schedule
DDPMでは\(\beta_t\)の一例として\(10^{-4}\)から\(0.02\)に線形に増加する値を利用していたが、\(\beta_t\)にはその他にも様々な定義が提案されている。ここでは幾つかの主要な定義について解説する。
linear schedule
DDPMで挙げられた基本的な\(\beta_t\)の定義は、\(10^{-4}\)から\(0.02\)に線形に増加する値である。
つまり、\(\beta_t\)は以下のように与えられる。
\begin{align} \beta_t := 10^{-4} + (0.02-10^{-4})\frac{t-1}{T-1} \end{align}
Stable Diffusionではsqrt_linearという名前で利用できる。
cosine schedule
2021年2月にOpenAIの技術者が発表した論文「Improved Denoising Diffusion Probabilistic Models」では、DDPMとは異なる\(\beta_t\)について検証された。検証された\(\beta_t\)は、累積の\(\alpha_t\)が三角関数になるよう定められる。
\begin{align} \begin{cases} f(t) &:= \left(\cos\left( \frac{t/T+0.008}{1+0.008}\frac{\pi}{2} \right)\right)^2 \\ \bar{\alpha}_t &:= \frac{f(t)}{f(0)} \\ \beta_t &:= \min\left(1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}},0.999\right) \\ \end{cases} \end{align}
Stable Diffusionではcosineという名前で利用できる。
quadratic linear schedule
現在Stable Diffusionの標準となっている\(\beta_t\)の設定は以下。
\begin{align} \beta_t := \left(\sqrt{0.00085} + (\sqrt{0.012}-\sqrt{0.00085})\frac{t-1}{T-1}\right)^2 \end{align}
Stable Diffusionでは(非常に紛らわしいが)linearという名前で利用でき、デフォルトの設定になっている。
スケジュールを変更するとモデル全体の再学習が必要になるので、Stable Diffusionの実行・学習ツールではほとんどの場合この設定しか使われない。
各beta scheduleの比較
それぞれの具体的な値の変化を視覚的に確認する。
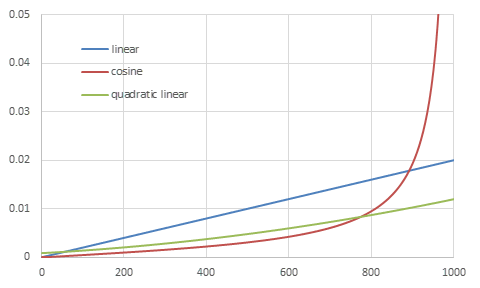
各beta scheduleの\(\beta_t\)
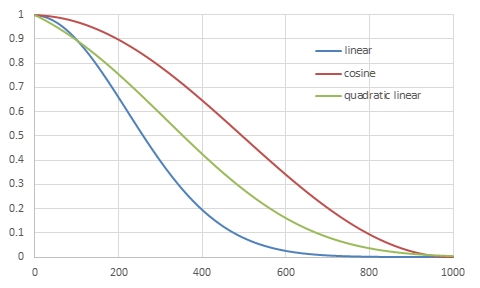
各beta scheduleの\(\alpha_t^2\)
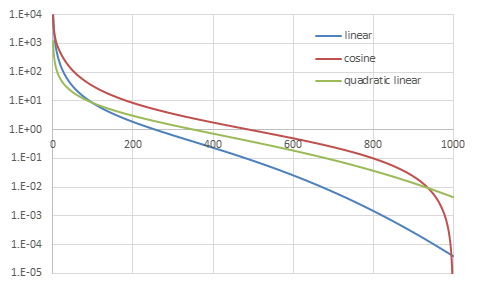
各beta scheduleの\(SNR(t)\) (\(\sigma_t^2=1-\alpha_t^2\)とした場合)
LDM
LDM(Latent Diffusion Model)は、2021年12月にミュンヘン大学のCompVisチームが公開した拡散モデルの実装。
以下の2点が特徴。
- 拡散モデルは画像そのものを直接入出力するのではなく、画像を復元することのできる情報を持つ潜在ベクトルを扱う。
- モデルにはCross-Attentionが導入され、promptなどの条件値を与えて画像を生成することが可能となった。
潜在ベクトルへの変換
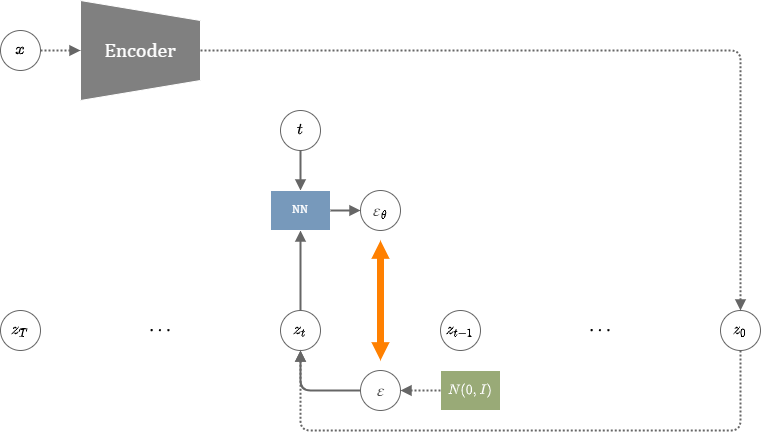
画像サイズ分の次元を直接扱うDDPMは、学習にも推論にも膨大な時間がかかるという問題があった。LDMは画像そのものではなく、より低次元の潜在ベクトルにDDPMを適用して学習することで、学習に要する時間を削減することに成功した。
低次元の圧縮にはオートエンコーダーを利用する。論文ではKL-VAE(=通常のVAE)と、VQ-VAEの2種類で実験を行っている。
潜在空間の中ではDDPMと同様の損失を用いて学習する。\(z_0\)を教師画像\(x\)をエンコーダーに通した潜在表現とすると、損失関数は以下のように表される。
\begin{align} Loss_{LDM} = \mathbb{E}_{z_0,\varepsilon,t}\left( \|\varepsilon - \varepsilon_\theta(z_t,t)\|^2 \right) \end{align}
条件付け
DDPM部分にはCross-Attentionモジュールを組み込んだU-Net型のモデルを使用する。
条件値\(c\)(=promptなど)はTransformerによってエンコードされ、U-NetのCross-AttentionモジュールにKey, Valueとして与えられる。
文章から画像を生成する実験では、LAION-400Mデータセットによって学習が行われた。
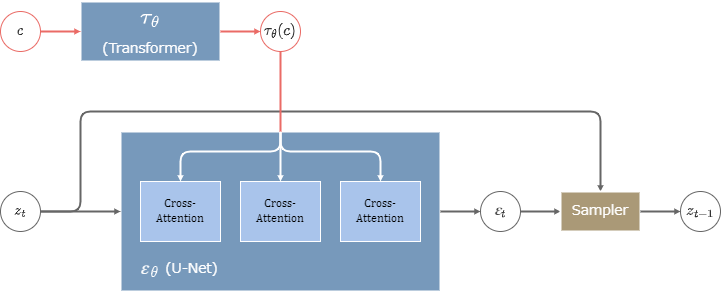
LDMのCross-Attention
CompVisチームは後に更に実用的なモデル「Stable Diffusion」を開発しているので、ここでは旧式にあたるLDMのモデル構造について詳しくは調べない。Stable Diffusionの構造についてはこのサイトで別途解説する。
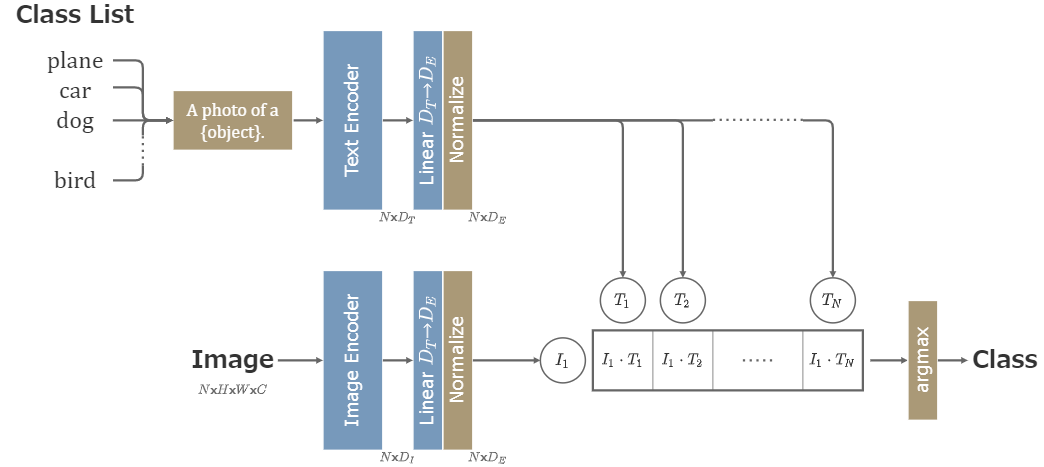
CLIP
CLIP(Contrastive Language-Image Pretraining)は2021年3月にOpenAIの技術者らによって論文が公開された画像分類のモデル。文章と画像をそれぞれエンコーダーで潜在表現に埋め込み、その内積によって文章と画像との類似度を測る仕組みが用いられている。特定のデータセットに特化した学習ではなく、OpenAIが独自に収集した4億ペアの画像と文章で構成されるWIT(Web Image Text)データセットで学習される。
ソースコードと学習済みのモデルファイルが公開されていて、現在自由に利用できる。
DDPMの派生技術ではないが、Stable DiffusionのText EncoderにCLIPが使われているのでここで解説する。
学習
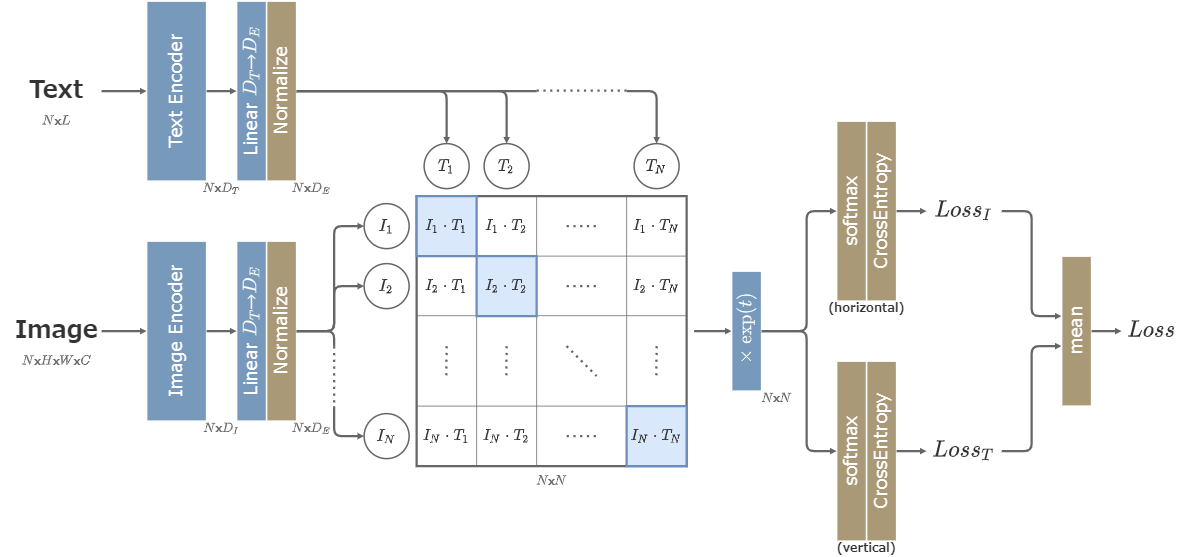
CLIPは以下のような構造を取る。
データセットには画像と、その画像を説明する文章がペアになって含まれている。CLIPの目的は、ペアになっている画像と文章を同じ次元に埋め込み、その値が近くなるようにすることである。
学習時はデータセットからN組のペアを取り出し、画像と文章をそれぞれImage EncoderとText Encoderに通す。
Image EncoderにはResNetあるいはViT (Vision Transformer)を用いる。
Text Encoderには12層のTransformer(の改造版)を用いる。\(D_T=512, L=76\)とする。
Image EncoderとText Encoderを通した値を全結合層によって同じ次元に揃え、正規化した後に全ての組み合わせの内積を取ることで\(N\times N\)行列が得られる。
行列の対角成分は、画像と文章が正しい組み合わせになっていて、それ以外は誤った組み合わせになっている。CLIPの目的は、行列の対角成分を大きな値に、それ以外の成分を小さな値にすることと言い換えることができる。
行列全体に温度パラメーター\(t\)の指数関数を掛け、softmaxを取ってCross Entropy Lossを取る。この際、画像方向と文章方向のCross Entropy Lossをそれぞれ取り、最後に平均を取って最終的な損失関数とする。
この学習方法は、画像に対してそのクラスや説明文章を予測するのではなく、N個の文章から正解となるものを選ぶN択問題になっている。深層学習モデルにとっては、画像の説明文章を正確に予測するよりも、N個の候補の中から1つ選択する方が簡単な問題になっている。
このようにデータ同士を比較して、似たデータを近付け、似ていないデータを遠ざけるような学習方法をContrastive Learningと言う。Contrastive Learningはラベルのない大量データを使った事前学習などでよく使われる。
推論
CLIPの画像分類タスクへの適用は以下のように実装される。
まず、分類対象となる全てのクラスに対して、「A photo of a plane.」「A photo of a car.」…というように文章を用意する。そして、それぞれの文章をText Encoderに通して各クラスに対応する潜在ベクトルを計算しておく。
「plane」といった単語そのものではなく、「A photo of a plane.」という文章にするのは、その方が分類の精度が高くなることが実験で確認されたからである。
次に分類したい画像をImage Encoderで埋め込む。
画像の潜在ベクトルに対して、先に計算した全てのクラスの潜在ベクトルとの内積を取り、最も大きい値となったクラスを予測クラスとする。
参考
- [2107.00630] Variational Diffusion Models
- [2010.02502] Denoising Diffusion Implicit Models (DDIM)
- [2102.09672] Improved Denoising Diffusion Probabilistic Models
- [1907.05600] Generative Modeling by Estimating Gradients of the Data Distribution (Score-based generative modeling)
- [2105.05233] Diffusion Models Beat GANs on Image Synthesis (classifier guidance)
- [2207.12598] Classifier-Free Diffusion Guidance (CFG)
- [2112.10752] High-Resolution Image Synthesis with Latent Diffusion Models (LDM)
- [2103.00020] Learning Transferable Visual Models From Natural Language Supervision (CLIP)
解説
- [2208.11970] Understanding Diffusion Models: A Unified Perspective
- [2305.08891] Common Diffusion Noise Schedules and Sample Steps are Flawed
- 岡野原大輔 - 拡散モデル
- DiffusionによるText2Imageの系譜と生成画像が動き出すまで - Speaker Deck
- Stable Diffusion を基礎から理解したい人向け論文攻略ガイド【無料記事】
- 拡散モデルの整理 - Qiita
- Denoising Diffusion Implicit Models (DDIM) Sampling
- 【論文メモ】High-Resolution Image Synthesis with Latent Diffusion Models (Stable Diffusion) - Qiita
- 【論文解説】自然言語処理と画像処理の融合 – OpenAI 『CLIP』を理解する | 楽しみながら理解するAI・機械学習入門