拡散モデルのサンプラー - まとめ・Timestep Scheduler
この記事ではこれまで紹介した拡散モデルのサンプラーを比較し、それらの類似性について考察する。
また、タイムステップに対するノイズの量を定めるNoise Schedulerについても紹介する。
関連記事
- DDPM: Denoising Diffusion Probabilistic Models
- DDPMの関連技術
- Stable Diffusionのモデル構造
- 拡散モデルの確率微分方程式
- 拡散モデルのサンプラー (1) - 離散過程・古典的数値計算法・LMS
- 拡散モデルのサンプラー (2) - DPM-Solver
- 拡散モデルのサンプラー (3) - UniPC
- 拡散モデルのサンプラー - まとめ・Timestep Scheduler (本記事)
目次
サンプラーのまとめ
これまで解説したサンプラーのアルゴリズムを以下にまとめる。
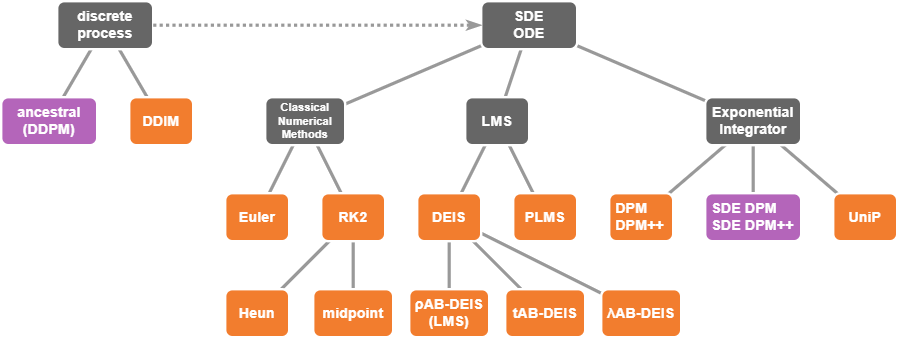
サンプラーの分類
| ODE/SDE | order | Single/Multi | Solver | 実装 |
|---|---|---|---|---|
| ODE | 1 | Singlestep | Euler =DDIM =DPM-Solver-1 =DPM-Solver++ | Euler |
| 2 | Singlestep | Heun | Heun | |
| midpoint | ||||
| DPM-Solver-2 | DPM2 | |||
| DPM-Solver++(2S) | ||||
| Multistep | DPM-Solver++2M | DPM++ 2M | ||
| 3 | Singlestep | DPM-Solver-3 | ||
| p | Multistep | LMS | LMS | |
| DEIS | ||||
| PLMS | PLMS | |||
| SDE | 1 | Singlestep | DDPM =SDE-DPM-Solver++1 | Euler a |
| SDE-DPM-Solver-1 | ||||
| 2 | Multistep | SDE-DPM-Solver-2M | ||
| SDE-DPM-Solver++(2M) | DPM++ 2M SDE |
サンプラーの中には互いに類似性のあるものもある。それらについて以下で考察する。
収束次数1のODEサンプラー
既に確認したように、上の表の収束次数1のODEサンプラーは全て同じアルゴリズムである。
- \(s<t\)
- \(\bar{y}_t\)が既に生成されていて、真の\(y_t\)との差が\(\bar{y}_t - y_t = \mathcal{O}(h^2)\)
- \(\varepsilon_\theta(y_t,t)\)が\(y_t\)に対してLipschitz連続
とする。
このとき、\(\bar{y}_s\)を次のように生成する。
\begin{align} \bar{y}_s = \bar{y}_t + (\varsigma_s - \varsigma_t)\varepsilon(\bar{y}_t) \end{align}
収束次数2のSinglestep ODEサンプラー
上の表の収束次数2のSinglestep ODEサンプラーは全て以下のパターンに含まれる。
- \(s<t\)
- \(h:=\lambda_s-\lambda_t\)
- \(\bar{y}_t\)が既に生成されていて、真の\(y_t\)との差が\(\bar{y}_t - y_t = \mathcal{O}(h^3)\)
- \(\varepsilon_\theta(y_t,t)\)が\(y_t\)に対してLipschitz連続
とする。
このとき、\(\bar{y}_s\)を次のように生成する。
\begin{align} \begin{cases} \bar{y}_r &= \bar{y}_t + (\varsigma_r-\varsigma_t)\varepsilon(\bar{y}_t) \\ \bar{y}_s &= \bar{y}_t + \left(\varsigma_s-\varsigma_t\right)\left( \varepsilon(\bar{y}_t) + \frac{1+u(h)}{2k}\left( \varepsilon(\bar{y}_r)-\varepsilon(\bar{y}_t) \right) \right) \\ \end{cases} \end{align}
ただし、\(k\)は\(k\neq 0\)となる任意の実数であり、\(r:=\lambda^{-1}(\lambda_t+kh)\)。
\(u(h)\)は\(u(h)=\mathcal{O}(h)\)を満たす任意の関数。
\(\varsigma_s-\varsigma_t\)と\(\varepsilon(\bar{y}_r)-\varepsilon(\bar{y}_t)\)がそれぞれ\(\mathcal{O}(h)\)のオーダーなので、\(u(h)=\mathcal{O}(h)\)であることからこのアルゴリズムはDPM-Solver-2と同じ収束次数になる。つまり2次収束するということになる。
DPM-Solver-2では\(u(h)=0\)、DPM-Solver++(2S) では\(u(h)=e^{-kh}-1\)となる。
2次Runge-Kutta法(RK2)は少し式の変換が必要なので以下で見ていく。
2次Runge-Kutta法
\(\tilde{k}\neq 0\)に対して\(\varsigma_r=\varsigma_t+\tilde{k}(\varsigma_s-\varsigma_t)\)とすると、RK2は次のように表される。
\begin{align} \begin{cases} \bar{y}_r &= \bar{y}_t + (\varsigma_r-\varsigma_t)\varepsilon(\bar{y}_t) \\ \bar{y}_s &= \bar{y}_t + \left(\varsigma_s-\varsigma_t\right)\left( \varepsilon(\bar{y}_t) + \frac{1}{2\tilde{k}}\left( \varepsilon(\bar{y}_r)-\varepsilon(\bar{y}_t) \right) \right) \\ \end{cases} \end{align}
\(\tilde{k}\)は\(\varsigma\)の中で取った割合の値なので、\(\lambda\)の中で取った割当である\(k\)とは異なる値である。
\(\tilde{k}\)から導かれる\(r\)と、\(k\)から導かれる\(r\)が同じ値になるように、\(\tilde{k}\)を\(k\)で表すことを試みる。
\begin{align} \varsigma_t+\tilde{k}(\varsigma_s-\varsigma_t) &= \varsigma_r \\ &= \exp(-\lambda_r) \\ &= \exp\left(-(\lambda_t+kh)\right) \\ &= \varsigma_te^{-kh} \\ \end{align}
よって、
\begin{align} \frac{k}{\tilde{k}} &= \frac{k(\varsigma_s-\varsigma_t)}{\varsigma_t\left(e^{-kh}-1\right)} \\ &= \frac{k(e^{-h}-1)}{e^{-kh}-1} \\ \end{align}
となり、RK2は以下のようになる。
\begin{align} \bar{y}_s &= \bar{y}_t + \left(\varsigma_s-\varsigma_t\right)\left( \varepsilon(\bar{y}_t) + \frac{1}{2k}\frac{k(e^{-h}-1)}{e^{-kh}-1}\left( \varepsilon(\bar{y}_r)-\varepsilon(\bar{y}_t) \right) \right) \\ \end{align}
\(\frac{k(e^{-h}-1)}{e^{-kh}-1}-1=\mathcal{O}(h)\)であることを示せば良い。
\(\xi:=e^{-kh}-1\)とする。
\(\xi=\mathcal{O}(h)\)なので、
\begin{align} \frac{k(e^{-h}-1)}{e^{-kh}-1} &= \frac{k}{\xi}\left( (\xi+1)^{1/k}-1 \right) \\ &= \frac{k}{\xi}\left(1+\frac{\xi}{k}+\mathcal{O}(\xi^2)-1 \right) \\ &= \frac{k}{\xi}\left(\frac{\xi}{k}+\mathcal{O}(\xi^2) \right) \\ &= 1+\mathcal{O}(\xi) \\ &= 1+\mathcal{O}(h) \\ \end{align}
となって、\(\frac{k(e^{-h}-1)}{e^{-kh}-1}-1=\mathcal{O}(h)\)となることがわかる。
収束次数1のSDEサンプラー
上の表の収束次数1のSDEサンプラーは、どちらもEuler法で生成してからノイズを調整するというancestral samplingになっている。両者をまとめると以下のパターンで表すことができる。
- \(s<t\)
- \(h:=\lambda_s-\lambda_t\)
- \(\bar{y}_t\)が既に生成されていて、真の\(y_t\)との差が\(\bar{y}_t - y_t = \mathcal{O}(h^2)\)
- \(\varepsilon_\theta(y_t,t)\)が\(y_t\)に対してLipschitz連続
とする。
このとき、\(\bar{y}_s\)を次のように生成する。
\begin{align} \bar{y}_s &= \bar{y}_t + \left(\frac{\varsigma_s^2}{\varsigma_t}+u(h^2)-\varsigma_t\right)\varepsilon(\bar{y}_t) + \sqrt{\varsigma_s^2-\left(\frac{\varsigma_s^2}{\varsigma_t}+v(h^2)\right)^2}n \\ \end{align}
ただし、\(n\sim\mathcal{N}(0,I)\)。
\(u(h^2), v(h^2)\)は\(u(h)=\mathcal{O}(h^2), v(h)=\mathcal{O}(h^2)\)を満たす任意の関数。
SDE-DPM-Solver++1(=DDPM)では、\(u(h^2)=v(h^2)=0\)。
SDE-DPM-Solver-1の場合は以下で詳しく調べる。
SDE-DPM-Solver-1
SDE-DPM-Solver-1のアルゴリズムは以下。
\begin{align} \bar{y}_s &= \bar{y}_t + 2 \left(\varsigma_s-\varsigma_t\right)\varepsilon(\bar{y}_t) + \sqrt{ \varsigma_t^2-\varsigma_s^2 }n \\ &= \bar{y}_t + \left(\frac{\varsigma_s^2}{\varsigma_t} + \left(2\varsigma_s-\varsigma_t-\frac{\varsigma_s^2}{\varsigma_t}\right) - \varsigma_t\right)\varepsilon(\bar{y}_t) + \sqrt{ \varsigma_s^2-\left(\frac{\varsigma_s^2}{\varsigma_t} + \sqrt{2\varsigma_s^2-\varsigma_t^2} - \frac{\varsigma_s^2}{\varsigma_t}\right)^2 }n \\ \end{align}
\(2\varsigma_s-\varsigma_t-\frac{\varsigma_s^2}{\varsigma_t}\)と\(\sqrt{2\varsigma_s^2-\varsigma_t^2} - \frac{\varsigma_s^2}{\varsigma_t}\)がそれぞれ\(\mathcal{O}(h^2)\)になることを示せば良い。
\(\tilde{h}:=\varsigma_s-\varsigma_t\)とすると、
\begin{align} \frac{\varsigma_s^2}{\varsigma_t} &= \frac{(\varsigma_t+\tilde{h})^2}{\varsigma_t} \\ &= \varsigma_t + 2\tilde{h} + \mathcal{O}(\tilde{h}^2) \\ \end{align}
また、
\begin{align} \sqrt{2\varsigma_s^2-\varsigma_t^2} &= \sqrt{2(\varsigma_t+\tilde{h})^2-\varsigma_t^2} \\ &= \sqrt{2(\varsigma_t+0)^2-\varsigma_t^2} + \tilde{h}\frac{2(\varsigma_t+0)}{\sqrt{2(\varsigma_t+0)^2-\varsigma_t^2}} + \mathcal{O}(\tilde{h}^2) \\ &= \varsigma_t + 2\tilde{h} + \mathcal{O}(\tilde{h}^2) \\ \end{align}
\(\tilde{h}=\varsigma_s-\varsigma_t=\varsigma_t(e^h-1)=\mathcal{O}(h)\)なので、
\begin{align} 2\varsigma_s-\varsigma_t-\frac{\varsigma_s^2}{\varsigma_t} &= 2(\varsigma_t+\tilde{h})-\varsigma_t-\left(\varsigma_t + 2\tilde{h} + \mathcal{O}(\tilde{h}^2)\right) \\ &= 2\varsigma_t+2\tilde{h}-\varsigma_t-2\tilde{h} + \mathcal{O}(\tilde{h}^2) \\ &= \mathcal{O}(\tilde{h}^2) \\ &= \mathcal{O}(h^2) \\ \end{align}
\begin{align} \sqrt{2\varsigma_s^2-\varsigma_t^2} - \frac{\varsigma_s^2}{\varsigma_t} &= (\varsigma_t + 2\tilde{h} + \mathcal{O}(\tilde{h}^2))-(\varsigma_t + 2\tilde{h} + \mathcal{O}(\tilde{h}^2)) \\ &= \mathcal{O}(\tilde{h}^2) \\ &= \mathcal{O}(h^2) \\ \end{align}
となることがわかる。
Timestep Scheduler
サンプラーに関する幾つかの論文ではサンプリングを行うタイムステップの列\(\{t_i\}_{i=0}^I\)についても論じられている。
\(t\)と\(\varsigma_t\)は1対1なので、\(\{t_i\}_{i=0}^I\)を選ぶということは\(\{\varsigma_{t_i}\}_{i=0}^I\)を選ぶということと同義である。このような列の選び方のことをTimestep Scheduler(あるいはNoise Scheduler)と呼ぶ。
以下では、タイムステップを\(0 = t_I < t_{I-1} < \cdots < t_1 < t_0 = 1\)となるように選ぶ前提とする。
t-uniform
\(t\)が等分されるように分割する。
具体的には、\([0, 1]\)の区間を\(I\)分割する。
\begin{align} t_i &= 1-\frac{i}{I} \end{align}
あるいは、\([t_{min}, 1]\)の区間を\(I-1\)分割する。(\(t_{min}=1/T\))
\begin{align} \begin{cases} t_I &= 0 \\ t_i &= 1 + \frac{i}{I-1}(t_{min}-1) \qquad (i<I) \end{cases} \end{align}
λ-uniform
DPM-Solverで提案されたスケジューラー。\(\lambda\)が等分されるように分割する。
具体的には、\([\lambda_{1},\lambda_{t_{min}}]\)の区間を\(I-1\)分割する。(\(\lambda_0=-\log 0=\infty\)なので、\([\lambda_1,\lambda_0]\)を\(I\)分割することはできない)
\begin{align} \begin{cases} t_I &= 0 \\ t_i &= \lambda^{-1}\left( \lambda_1 + \frac{i}{I-1}(\lambda_{t_{min}}-\lambda_1) \right) \qquad (i<I) \end{cases} \end{align}
AUTOMATIC1111では名前にExponentialと付くサンプラーがこのノイズスケジューラーを用いている。
Polynomial
NVIDIAのKarrasらが2022年6月に発表した論文で提案したスケジューラー。
\(\varsigma_{t_i}\)が以下の値になるように定める。
\begin{align} \begin{cases} t_I &= 0 \\ \varsigma_{t_i} &= \left( \varsigma_1^{1/\rho} + \frac{i}{I-1}(\varsigma_{t_{min}}^{1/\rho}-\varsigma_1^{1/\rho}) \right)^\rho \qquad (i<I) \end{cases} \end{align}
\(\rho=7\)を選ぶのが最善とされている。
AUTOMATIC1111では名前にKarrasと付くサンプラーがこのスケジューラーを用いている。
λ-uniformとの関係
\(\xi:=1/\rho\)とする。
\(\rho\rightarrow\infty\)、つまり\(\xi\rightarrow 0\)とすると、l'Hôpitalの定理を用いて、
\begin{align} \lim_{\xi\rightarrow0}\lambda_{t_i} &= \lim_{\xi\rightarrow0}\left( -\log\left( \left( \varsigma_1^{1/\rho} + \frac{i}{I-1}(\varsigma_{t_{min}}^{1/\rho}-\varsigma_1^{1/\rho}) \right)^\rho \right) \right) \\ &= \lim_{\xi\rightarrow0}\left( -\rho\log \left( \varsigma_1^{1/\rho} + \frac{i}{I-1}(\varsigma_{t_{min}}^{1/\rho}-\varsigma_1^{1/\rho}) \right) \right) \\ &= \lim_{\xi\rightarrow0}\left( -\frac{\log \left( \varsigma_1^\xi + \frac{i}{I-1}(\varsigma_{t_{min}}^\xi-\varsigma_1^\xi) \right)}{\xi} \right) \\ &= \lim_{\xi\rightarrow0}\left( -\frac{\frac{d}{d\xi}\log\left( \varsigma_1^\xi + \frac{i}{I-1}(\varsigma_{t_{min}}^\xi-\varsigma_1^\xi) \right)}{1} \right) \\ &= \lim_{\xi\rightarrow0}\left( -\frac{\varsigma_1^\xi\log\varsigma_1 + \frac{i}{I-1}(\varsigma_{t_{min}}^\xi\log\varsigma_{t_{min}}-\varsigma_1^\xi\log\varsigma_1)}{\varsigma_1^\xi + \frac{i}{I-1}(\varsigma_{t_{min}}^\xi-\varsigma_1^\xi)} \right) \\ &= -\frac{1\cdot\log\varsigma_1 + \frac{i}{I-1}(1\cdot\log\varsigma_{t_{min}}-1\cdot\log\varsigma_1)}{1 + \frac{i}{I-1}(1-1)} \\ &= \lambda_1 + \frac{i}{I-1}(\lambda_{t_{min}}-\lambda_1) \\ \end{align}
となる。
よって、λ-uniformは\(\rho=\infty\)としたときのPolynomialと解釈することができる。
比較
Stable Diffusionの\(\beta_t\)から構成される\(\varsigma_t\)について、各スケジューラーの差異を以下のグラフに示す。
横軸は\(\frac{i}{I-1}\)であり、縦軸は\(\varsigma_{t_i}\)である。
薄い赤色の線は最も上の直線状のものが\(\rho=1\)のPolynomialで、下に下がるほど\(\rho\)の値が上がっていく。
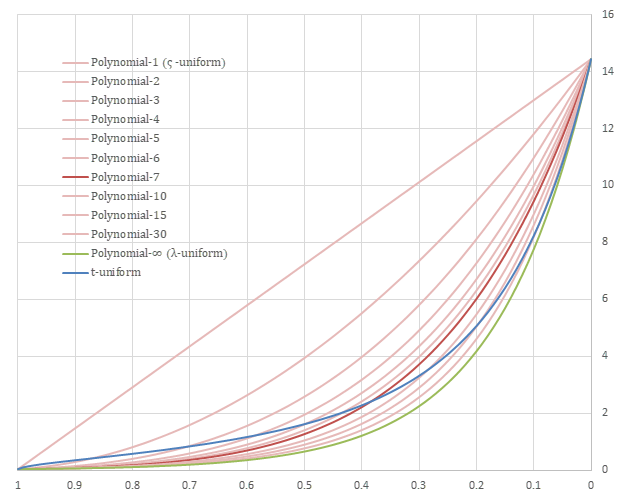
スケジューラーの比較