拡散モデルのサンプラー (1) - 離散過程・古典的数値計算法・LMS
この記事では拡散モデルの生成過程で使われるサンプラーと呼ばれる様々なアルゴリズムを解説する。
関連記事
- DDPM: Denoising Diffusion Probabilistic Models
- DDPMの関連技術
- Stable Diffusionのモデル構造
- 拡散モデルの確率微分方程式
- 拡散モデルのサンプラー (1) - 離散過程・古典的数値計算法・LMS (本記事)
- 拡散モデルのサンプラー (2) - DPM-Solver
- 拡散モデルのサンプラー (3) - UniPC
- 拡散モデルのサンプラー - まとめ・Timestep Scheduler
目次
前提
表記
前の記事で確認したようにVP SDEとVE SDEは相互に変換可能なので、表記を簡単にするためにVE SDEの前提で話を進める。
(\(\varsigma_t\)という表記は一般的ではなく、\(\varsigma_t\)に相当する値は単に\(\sigma_t\)あるいは\(t\)と表されることが多いが、混乱を避けるためにこの投稿では\(\varsigma_t\)という表記を使うことにする。)
\begin{align} \begin{cases} y_t &:= \frac{x_t}{\alpha_t} \\ \varsigma_t &:= \frac{\sigma_t}{\alpha_t} \end{cases} \end{align}
また、以下のような表記を用いる。
- \(\varepsilon_\theta(x_t, t)=\varepsilon_\theta(\alpha_ty_t, t)\)を単に\(\varepsilon(y_t, t)\)と表記する。
- 添字によって時刻が明らかな場合は更に\(\varepsilon(y_t)\)と省略。
- 方程式の真の解を\(y_t\)と表し、近似解を\(\bar{y}_t\)と表す。
- タイムステップ\(t\)までの生成結果\(\bar{y}_t\)を用いて、新たなタイムステップ\(s<t\)の値\(\bar{y}_s\)を生成する生成過程(逆仮定)を考える。
- 更に前のタイムステップは\(s<t<u<\cdots\)と表す。
- \(s=t_{i+1}<t=t_i<t_{i-1}<t_{i-2}<\cdots\)とも表す場合もある。
- \(s\)と\(t\)との間にタイムステップを取る必要がある場合は\(r\)と表す。
(生成される順番は\(t\)→\(r\)→\(s\)となるが、必ずしも\(s<r<t\)になるわけではない)
拡散過程・SDE・ODE
DDPMの拡散過程は\(x_t=\alpha_t x_0+\sigma_t\varepsilon\)なので、\(y, \varsigma\)表記に書き改めると
\begin{align} y_t &= \frac{x_t}{\alpha_t} \\ &= \frac{1}{\alpha_t}\left( \alpha_t x_0+\sigma_t\varepsilon \right) \\ &= x_0+\varsigma_t\varepsilon \\ &= y_0+\varsigma_t\varepsilon \\ \end{align}
となる。(\(\varepsilon\sim\mathcal{N}(0,I)\))
また、以前の考察によると、\(y, \varsigma\)表記のSDEとODEは次のように表される。
\begin{align} dy_t &= \sqrt{\frac{d}{dt}\frac{\sigma_t^2}{\alpha_t^2}}dw_t \\ &= \sqrt{\frac{d\varsigma_t^2}{dt}}dw_t \\ \end{align}
\begin{align} dy_t &= -\sigma_t\nabla_{x_t} \log p_t(x_t) d\varsigma_t \\ \end{align}
スコアと予測ノイズの関係によると、十分学習されたノイズ予測ニューラルネットワーク\(\varepsilon_\theta(x_t,t)\)とスコア\(\nabla_{x_t}\log p_t(x_t)\)との間には、
\begin{align} -\sigma_t\nabla_{x_t}\log p_t(x_t) \sim \varepsilon_\theta(x_t,t) \end{align}
という関係が成り立つので、ODEは次のように表すこともできる。
\begin{align} dy_t &= -\sigma_t\nabla_{x_t} \log p_t(x_t) d\varsigma_t \\ &\sim \varepsilon_\theta(x_t,t) d\varsigma_t \\ &= \varepsilon(y_t) d\varsigma_t \\ \end{align}
\(y, \varsigma\)表記の拡散過程は
\begin{align} y_t = y_0+\varsigma_t\varepsilon \end{align}
であり、SDEとODEは次のようになる。
\begin{align} \begin{cases} dy_t &= \sqrt{\frac{d\varsigma_t^2}{dt}}dw_t \qquad \text{(SDE)} \\ dy_t &= \varepsilon(y_t) d\varsigma_t \qquad \text{(probability flow ODE)} \\ \end{cases} \end{align}
離散過程
DDPM
DDPMの関連技術の記事で求めたように、離れたタイムステップ間のDDPMの条件付き確率は以下のように表される。(\(s<t\))
\begin{align} q(x_s|x_t,x_0) = p_\mathcal{N}\left( x_s \middle| \tilde{\mu}_{s|t}(x_t,x_0), \tilde{\beta}_{s|t}I \right) \\ \begin{cases} \tilde{\mu}_{s|t}(x_t,x_0) &= \alpha_sx_0 + \sqrt{\sigma_s^2 - \tilde{\beta}_{s|t}}\frac{ x_t - \alpha_tx_0 }{\sigma_t} \\ \tilde{\beta}_{s|t} &= \frac{\sigma_{t|s}^2\sigma_s^2}{\sigma_t^2} \\ \end{cases} \end{align}
したがって、\(n\sim\mathcal{N}(0,I)\)とすると、
\begin{align} x_s &= \tilde{\mu}_{s|t}(x_t,x_0) + \sqrt{\tilde{\beta}_{s|t}}n \\ \end{align}
また、\(x_t \sim \alpha_t x_0 + \sigma_t\varepsilon_\theta(x_t,t)\)を用いて、
\begin{align} x_s &= \tilde{\mu}_{s|t}(x_t,x_0) + \sqrt{\tilde{\beta}_{s|t}}n \\ &= \alpha_sx_0 + \sqrt{\sigma_s^2 - \tilde{\beta}_{s|t}}\frac{ x_t - \alpha_tx_0 }{\sigma_t} + \sqrt{\tilde{\beta}_{s|t}}n \\ &\sim \alpha_s\frac{x_t - \sigma_t\varepsilon_\theta(x_t,t)}{\alpha_t} + \sqrt{\sigma_s^2 - \tilde{\beta}_{s|t}}\varepsilon_\theta(x_t,t) + \sqrt{\tilde{\beta}_{s|t}}n \\ &= \alpha_s\left( \frac{x_t}{\alpha_t} - \frac{\sigma_t}{\alpha_t}\varepsilon_\theta(x_t,t) \right) + \sqrt{\sigma_s^2 - \frac{\sigma_{t|s}^2\sigma_s^2}{\sigma_t^2}}\varepsilon_\theta(x_t,t) + \sqrt{\frac{\sigma_{t|s}^2\sigma_s^2}{\sigma_t^2}}n \\ &= \alpha_s\left( \frac{x_t}{\alpha_t} - \frac{\sigma_t}{\alpha_t}\varepsilon_\theta(x_t,t) \right) + \sqrt{\sigma_s^2 - \frac{\left(\sigma_t^2-\frac{\alpha_t^2}{\alpha_s^2}\sigma_s^2\right)\sigma_s^2}{\sigma_t^2}}\varepsilon_\theta(x_t,t) + \sqrt{\frac{\left(\sigma_t^2-\frac{\alpha_t^2}{\alpha_s^2}\sigma_s^2\right)\sigma_s^2}{\sigma_t^2}}n \\ &= \alpha_s\left( \frac{x_t}{\alpha_t} - \frac{\sigma_t}{\alpha_t}\varepsilon_\theta(x_t,t) \right) + \sqrt{\frac{\sigma_s^2/\alpha_s^2}{\sigma_t^2/\alpha_t^2}\sigma_s^2}\varepsilon_\theta(x_t,t) + \sqrt{\frac{\sigma_s^2}{\sigma_t^2/\alpha_t^2}\left(\frac{\sigma_t^2}{\alpha_t^2}-\frac{\sigma_s^2}{\alpha_s^2}\right)}n \\ \end{align}
となる。
\(y_t, \varsigma_t\)の表記に書き直すと以下を得る。
\begin{align} y_s &= y_t - \varsigma_t\varepsilon(y_t) + \sqrt{\frac{\varsigma_s^2}{\varsigma_t^2}\varsigma_s^2}\varepsilon(y_t) + \sqrt{\frac{\varsigma_s^2}{\varsigma_t^2}\left(\varsigma_t^2-\varsigma_s^2\right)}n \\ &= y_t + \frac{\varsigma_s^2 - \varsigma_t^2}{\varsigma_t}\varepsilon(y_t) + \sqrt{\frac{\varsigma_s^2}{\varsigma_t^2}\left(\varsigma_t^2-\varsigma_s^2\right)}n \\ \end{align}
- \(s<t\)
- \(\bar{y}_t\)が既に生成されている
とする。
このとき、\(\bar{y}_s\)を次のように生成する。
\begin{align} \bar{y}_s = \bar{y}_t + \frac{\varsigma_s^2 - \varsigma_t^2}{\varsigma_t}\varepsilon(\bar{y}_t) + \sqrt{\frac{\varsigma_s^2}{\varsigma_t^2}\left(\varsigma_t^2-\varsigma_s^2\right)}n \end{align}
ただし、\(n\sim\mathcal{N}(0,I)\)。
ancestral sampling
後述のEuler法を用いると、DDPMは以下のようにも表すことができる。
\begin{align} \bar{y}_s &= \bar{y}_t + \frac{\varsigma_s^2 - \varsigma_t^2}{\varsigma_t}\varepsilon(\bar{y}_t) + \sqrt{\frac{\varsigma_s^2}{\varsigma_t^2}\left(\varsigma_t^2-\varsigma_s^2\right)}n \\ &= \bar{y}_t + \left(\frac{\varsigma_s^2}{\varsigma_t} - \varsigma_t\right)\varepsilon(\bar{y}_t) + \sqrt{\varsigma_s^2 - \left(\frac{\varsigma_s^2}{\varsigma_t}\right)^2}n \\ &= Euler\left(\bar{y}_t, \varsigma_t\rightarrow\frac{\varsigma_s^2}{\varsigma_t}\right) + \sqrt{\varsigma_s^2 - \left(\frac{\varsigma_s^2}{\varsigma_t}\right)^2}n \\ \end{align}
これはタイムステップ\(\varsigma_s\)に対応する値を直接生成するのではなく、1段階目で\(\varsigma_s^2/\varsigma_t\)まで通常よりも大幅にタイムステップを進め、進みすぎたタイムステップ分のノイズを2段階目で\(\varsigma_s\)に修正しているものと捉えることができる。
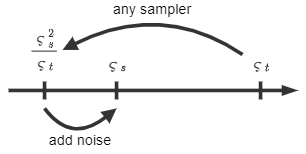
ancestral samplingの概要
Euler法の部分は他の任意のサンプラーに置き換えることができる。
このようなサンプリングの方法はAncestral Samplingと呼ばれていて、DDPMのサンプリング方法もAUTOMATIC1111ではEuler aと名付けられている。(aはancestralを意味する)
Ancestral Samplingと同様に、「\(y_t\)→\(y_r\)の予測」・「\(y_r\)→\(y_s\)のノイズ付与」の2段階で生成するような類似のアルゴリズムが幾つか存在する。それらを次の表にまとめる。
| 名称 | \(\varsigma_r\) | \(\varsigma_r/\varsigma_s\) |
|---|---|---|
| DDIM (\(\eta=0\)) | \(\varsigma_r = \varsigma_s\) | \(\varsigma_r/\varsigma_s = 1\) |
| DDIM (\(\eta\in[0,1]\)) | \(\varsigma_r = \frac{\varsigma_s}{\varsigma_t}\sqrt{\varsigma_t^2-\eta^2(\varsigma_t^2-\varsigma_s^2)}\) | \(\varsigma_r/\varsigma_s = \sqrt{1-\eta^2\left(1-\left(\varsigma_s/\varsigma_t\right)^2\right)}\) |
| DDPM | \(\varsigma_r = \frac{\varsigma_s^2}{\varsigma_t}\) | \(\varsigma_r/\varsigma_s = \varsigma_s/\varsigma_t\) |
| LCM | \(\varsigma_r = \varsigma_0 = 0\) | \(\varsigma_r/\varsigma_s = 0\) |
| TCD | \(\varsigma_r = \varsigma_{(1-\gamma)s}\) | \(0\leq\varsigma_r/\varsigma_s\leq1\) |
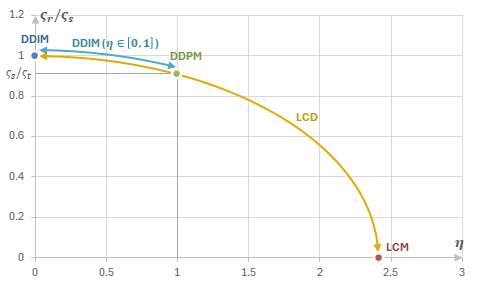
Ancestral Samplingの類似アルゴリズム
DDIM
DDPMの関連技術の記事でも解説したように、DDIM (\(\eta=0\))はDDPMからランダム性を取り除いた生成過程である。
\begin{align} x_s = \frac{\alpha_s}{\alpha_t}\left( x_t-\sigma_t\varepsilon_\theta(x_t, t) \right) + \sigma_s\varepsilon_\theta(x_t, t) \end{align}
\(y_t, \varsigma_t\)の表記に書き直すと以下を得る。
\begin{align} y_s &= y_t - \varsigma_t\varepsilon(y_t) + \varsigma_s\varepsilon(y_t) \\ &= y_t + (\varsigma_s - \varsigma_t)\varepsilon(y_t) \\ \end{align}
- \(s<t\)
- \(\bar{y}_t\)が既に生成されている
とする。
このとき、\(\bar{y}_s\)を次のように生成する。
\begin{align} \bar{y}_s = \bar{y}_t + (\varsigma_s - \varsigma_t)\varepsilon(\bar{y}_t) \end{align}
これはODE
\begin{align} dy_t = \varepsilon(y_t) d\varsigma_t \end{align}
に対する後述のEuler法と全く同じアルゴリズムである。
AUTOMATIC1111ではDDIMとEuler法が両方実装されている。サンプラーの基本的なアルゴリズムは同じであるはずだが、それぞれのサンプラーを用いた場合の生成結果は異なる。
その要因として考えられるのは、AUTOMATIC1111の実装ではDDIMのタイムステップの最大値が1000ではないということである。例えばステップ数が20のときのDDIMは、タイムステップ951から生成が始まる。
一般のDDIM
\(0<\eta<1\)の場合のDDIMについて考察する。この場合のDDIMの更新式は、
\begin{align} x_s &= \frac{\alpha_s}{\alpha_t}\left( x_t-\sigma_t\varepsilon_\theta(x_t, t) \right) + \sqrt{\sigma_s^2-\eta^2\tilde{\beta}_{s|t}}\varepsilon_\theta(x_t, t) + \eta\sqrt{\tilde{\beta}_{s|t}}n \\ \end{align}
となる。ただし、\(n\in\mathcal{N}(0,I)\)であり、\(\tilde{\beta}_{s|t}\)は
\begin{align} \tilde{\beta}_{s|t} &:= \frac{\sigma_{t|s}^2\sigma_s^2}{\sigma_t^2} \\ &= \frac{\sigma_s^2}{\sigma_t^2}\left( \sigma_t^2-\frac{\alpha_t^2}{\alpha_s^2}\sigma_s^2 \right) \\ &= \frac{\sigma_s^2}{\sigma_t^2}\alpha_t^2\left( \varsigma_t^2-\varsigma_s^2 \right) \\ &= \alpha_s^2\frac{\varsigma_s^2}{\varsigma_t^2}\left( \varsigma_t^2-\varsigma_s^2 \right) \\ \end{align}
である。
\(y\)の表記に書き換えると次のようになる。
\begin{align} y_s &= y_t-\varsigma_t\varepsilon_\theta(x_t, t) + \frac{1}{\alpha_s}\sqrt{\sigma_s^2-\eta^2\tilde{\beta}_{s|t}}\varepsilon_\theta(x_t, t) + \frac{1}{\alpha_s}\eta\sqrt{\tilde{\beta}_{s|t}}n \\ &= y_t-\varsigma_t\varepsilon_\theta(x_t, t) + \sqrt{\varsigma_s^2-\eta^2\frac{\varsigma_s^2}{\varsigma_t^2}\left( \varsigma_t^2-\varsigma_s^2 \right)}\varepsilon_\theta(x_t, t) + \eta\sqrt{\frac{\varsigma_s^2}{\varsigma_t^2}\left( \varsigma_t^2-\varsigma_s^2 \right)}n \\ &= y_t-\varsigma_t\varepsilon_\theta(x_t, t) + \frac{\varsigma_s}{\varsigma_t}\sqrt{\varsigma_t^2-\eta^2\left( \varsigma_t^2-\varsigma_s^2 \right)}\varepsilon_\theta(x_t, t) + \eta\frac{\varsigma_s}{\varsigma_t}\sqrt{\varsigma_t^2-\varsigma_s^2}n \\ \end{align}
\(s\rightarrow t-dt\)として離散の更新式を連続化する。
\begin{align} dy_t = y_t-y_s &= \varsigma_t\varepsilon_\theta(x_t, t) - \frac{\varsigma_s}{\varsigma_t}\sqrt{\varsigma_t^2-\eta^2\left( \varsigma_t^2-\varsigma_s^2 \right)}\varepsilon_\theta(x_t, t) - \eta\frac{\varsigma_s}{\varsigma_t}\sqrt{\varsigma_t^2-\varsigma_s^2}n \\ &\sim \varsigma_t\varepsilon_\theta(x_t, t) - \frac{\varsigma_s}{\varsigma_t}\sqrt{\varsigma_t^2-\eta^2\frac{d\varsigma_t^2}{dt}dt}\varepsilon_\theta(x_t, t) - \eta\frac{\varsigma_s}{\varsigma_t}\sqrt{\frac{d\varsigma_t^2}{dt}dt}n \\ &\sim \varsigma_t\varepsilon_\theta(x_t, t) - \varsigma_s\sqrt{1-\eta^2\frac{1}{\varsigma_t^2}\frac{d\varsigma_t^2}{dt}dt}\varepsilon_\theta(x_t, t) - \eta\sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &\sim \varsigma_t\varepsilon_\theta(x_t, t) - \varsigma_s\left( 1-\frac{1}{2}\eta^2\frac{1}{\varsigma_t^2}\frac{d\varsigma_t^2}{dt}dt \right)\varepsilon_\theta(x_t, t) - \eta\sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &= (\varsigma_t-\varsigma_s)\varepsilon_\theta(x_t, t) + \frac{\varsigma_s}{\varsigma_t}\frac{\eta^2}{2\varsigma_t}\frac{d\varsigma_t^2}{dt}\varepsilon_\theta(x_t, t)dt - \eta\sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &\sim \frac{d\varsigma_t}{dt}\varepsilon_\theta(x_t, t)dt + \frac{\eta^2}{2\varsigma_t}\frac{d\varsigma_t^2}{dt}\varepsilon_\theta(x_t, t)dt - \eta\sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &= \frac{1+\eta^2}{2\varsigma_t}\frac{d\varsigma_t^2}{dt}\varepsilon_\theta(x_t, t)dt - \eta\sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &= -\frac{1+\eta^2}{2\varsigma_t}\frac{d\varsigma_t^2}{dt}\sigma_t\nabla\log p_t(x_t)dt - \eta\sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &= -\alpha_t\frac{1+\eta^2}{2}\frac{d\varsigma_t^2}{dt}\nabla\log p_t(x_t)dt - \eta\sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ \end{align}
前回の投稿で求めた\(f(t)=\frac{1}{\alpha_t}\frac{d\alpha_t}{dt}, g(t)^2=\alpha_t^2\frac{d\varsigma_t^2}{dt}\)を用いると、
\begin{align} dy_t &= -\alpha_t\frac{1+\eta^2}{2}\frac{d\varsigma_t^2}{dt}\nabla\log p_t(x_t)dt - \eta\sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &= -\frac{1}{\alpha_t}\frac{1+\eta^2}{2}g(t)^2\nabla\log p_t(x_t)dt - \eta\frac{g(t)}{\alpha_t}d\bar{w}_t \\ \end{align}
\(x\)の式に再び戻すと以下のSDEに連続化される。
\begin{align} dx_t = d(\alpha_ty_t) &= \frac{d\alpha_t}{dt}y_tdt + \alpha_tdy_t \\ &= \frac{1}{\alpha_t}\frac{d\alpha_t}{dt}x_tdt -\frac{1+\eta^2}{2}g(t)^2\nabla\log p_t(x_t)dt - \eta g(t)d\bar{w}_t \\ &= \left( f(t)x_t - \frac{1+\eta^2}{2}g(t)^2\nabla\log p_t(x_t) \right)dt - \eta g(t)d\bar{w}_t \\ \end{align}
これは一般化reverse-time SDEにおいて、\(h(t)=-\eta g(t)\)としたものと一致する。
一般のDDIM (\(0≦\eta≦1\))は、このSDEを離散化したものである。
古典的数値計算法
この節ではODEにEuler法やHeun法などの古典的な数値計算法を適用したアルゴリズムを解説する。
ODEを再び以下に記載する。
\begin{align} dy_t = \varepsilon(y_t) d\varsigma_t \end{align}
Euler法
一般にODEが以下の式で表されているとする。
\begin{align} \frac{dy}{dt} = f(y, t) \end{align}
\(y(t+h)\)をTaylor展開すると、
\begin{align} y(t+h) &= y(t) + hy'(t) + \mathcal{O}(h^2) \\ &= y(t) + hf(y(t), t) + \mathcal{O}(h^2) \\ \end{align}
が成り立つ。
そこで、
\begin{align} y(t+h) \sim y(t) + hf(y(t), t) \end{align}
と見なして値を生成するアルゴリズムがEuler法である。
Euler法の誤差は\(\mathcal{O}(h^2)\)であり、このような性質を1次収束という。
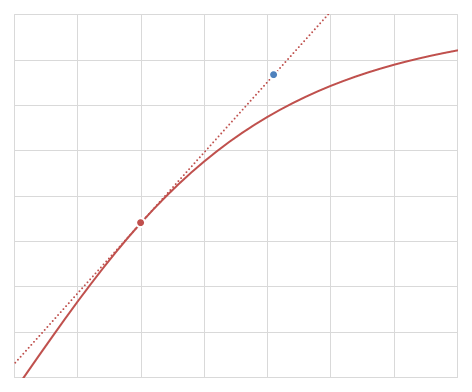
Euler法の例 (赤い点が\((t,y(t))\)で、青い点が\((t+h,y(t+h))\)のEuler法による近似)
Euler法を拡散モデルのODEに適用すると以下のようになる。(\(h=\varsigma_s-\varsigma_t, f=\varepsilon_\theta\))
\begin{align} \bar{y}_s = \bar{y}_t + (\varsigma_s-\varsigma_t)\varepsilon(\bar{y}_t) \end{align}
真の解\(y_t\)に対して\(\bar{y}_t-y_t=\mathcal{O}(h^2)\)であり、\(\varepsilon(y_t,t)\)が引数\(y_t\)に対してLipschitz連続であるとき、
\begin{align} y_s &= y_t + (\varsigma_s-\varsigma_t)\varepsilon(y_t) + \mathcal{O}(h^2) \\ &= \bar{y}_t + y_t-\bar{y}_t + (\varsigma_s-\varsigma_t)(\varepsilon(\bar{y}_t)+\varepsilon(y_t)-\varepsilon(\bar{y}_t)) + \mathcal{O}(h^2) \\ &= \bar{y}_t + \mathcal{O}(h^2) + (\varsigma_s-\varsigma_t)(\varepsilon(\bar{y}_t)+\mathcal{O}(y_t-\bar{y}_t)) + \mathcal{O}(h^2) \\ &= \bar{y}_t + (\varsigma_s-\varsigma_t)\varepsilon(\bar{y}_t) + \mathcal{O}(h^2) \\ &= \bar{y}_s + \mathcal{O}(h^2) \\ \end{align}
となるので、\(\bar{y}_s\)もまた真の解\(y_s\)に対して1次収束する。
拡散モデルのEuler法の例を以下の図に示す。
\(\{0.8, -0.3\}\)という2つの1次元値データセットによる拡散モデルを想定。ノイズ関数はStable Diffusionのものを使用。
薄い赤色の線は各初期値からODEを解いた真の解\(y_t\)によるprobability flowを表し、濃い赤色の線は\(y_1=0.3\)からEuler法によって生成するときの軌跡を表す。
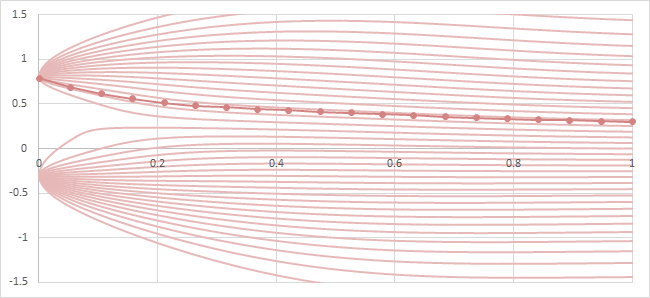
probability flowとEuler法の軌跡
このアルゴリズムはAUTOMATIC1111ではEulerという名前で実装されている。
- \(s<t\)
- \(h:=\varsigma_s-\varsigma_t\)
- \(\bar{y}_t\)が既に生成されていて、真の\(y_t\)との差が\(\bar{y}_t - y_t = \mathcal{O}(h^2)\)
- \(\varepsilon_\theta(y_t,t)\)が\(y_t\)に対してLipschitz連続
とする。
このとき、\(\bar{y}_s\)を次のように生成する。
\begin{align} \bar{y}_s = \bar{y}_t + (\varsigma_s-\varsigma_t)\varepsilon(\bar{y}_t) \end{align}
Heun法
一般にODEが以下の式で表されているとする。
\begin{align} \frac{dy}{dt} = f(y, t) \end{align}
\(y(t+h)\)をTaylor展開すると、
\begin{align} y(t+h) &= y(t) + hy'(t) + \frac{h^2}{2}y''(t) + \mathcal{O}(h^3) \\ &= y(t) + hf(y(t), t) + \frac{h^2}{2}\frac{d}{dt}f(y(t), t) + \mathcal{O}(h^3) \\ \end{align}
が成り立つ。\(f\)の微分は与えられていないので、何らかの方法で\(\frac{d}{dt}f(y(t), t)\)を近似する必要がある。
\(k\neq 0\)を取り、タイムステップ幅\(kh\)のEuler法
\begin{align} y(t+kh) = y(t) + khf(y(t),t) + \mathcal{O}(h^2) \end{align}
を\(t\)で微分する。
\begin{align} y'(t+kh) &= y'(t) + kh\frac{d}{dt}f(y(t),t) + \mathcal{O}(h^2) \\ f(y(t+kh), t+kh) &= f(y(t), t) + kh\frac{d}{dt}f(y(t),t) + \mathcal{O}(h^2) \\ \end{align}
タイムステップ幅\(kh\)のEuler法の生成値を\(\bar{y}(t+kh)\)と表すと、左辺はEuler法の収束次数が1であることを用いて以下のようになる。(\(f\)にLipschitz連続性の仮定が必要)
\begin{align} f(y(t+kh), t+kh) &= f(\bar{y}(t+kh)+y(t+kh)-\bar{y}(t+kh), t+kh) \\ &= f(\bar{y}(t+kh), t+kh) + \mathcal{O}(y(t+kh)-\bar{y}(t+kh)) \\ &= f(\bar{y}(t+kh), t+kh) + \mathcal{O}(h^2) \\ \end{align}
したがって、
\begin{align} h\frac{d}{dt}f(y(t),t) &= \frac{1}{k}\left(f(y(t+kh), t+kh) - f(y(t), t)\right) + \mathcal{O}(h^2) \\ &= \frac{1}{k}\left(f(\bar{y}(t+kh), t+kh) - f(y(t), t)\right) + \mathcal{O}(h^2) \\ \end{align}
となる。これを最初のTaylor展開の式に代入する。
\begin{align} y(t+h) &= y(t) + hf(y(t), t) + \frac{h^2}{2}\frac{d}{dt}f(y(t), t) + \mathcal{O}(h^3) \\ &= y(t) + hf(y(t), t) + \frac{h}{2}\left( \frac{1}{k}\left(f(\bar{y}(t+kh), t+kh) - f(y(t), t)\right) + \mathcal{O}(h^2) \right) + \mathcal{O}(h^3) \\ &= y(t) + h\left( \left(1-\frac{1}{2k}\right)f(y(t), t) + \frac{1}{2k}f(\bar{y}(t+kh), t+kh) \right) + \mathcal{O}(h^3) \\ \end{align}
このアルゴリズムを2次Runge-Kutta法と呼ぶ。
特に\(k=1/2\)としたものが中点法(midpoint method)であり、\(k=1\)としたものがHeun法である。Heun法を以下に記す。
\begin{align} y(t+h) &\sim y(t) + \frac{h}{2}\left( f(y(t), t) + f(\bar{y}(t+h), t+h) \right) \\ \end{align}
誤差は\(\mathcal{O}(h^3)\)なのでHeun法は2次収束し、生成の品質はEuler法より優れている。
その代わりに、1ステップにつき2回の\(f=\varepsilon_\theta\)の関数評価が必要になり、同じステップ数でも2倍の生成時間がかかるという欠点がある。
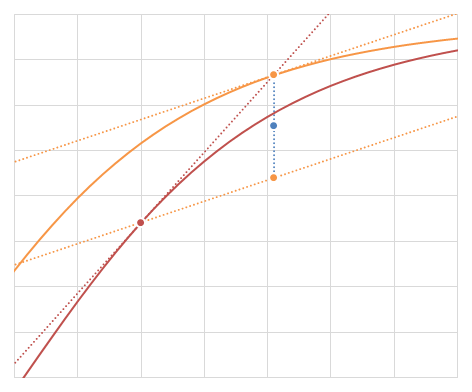
Heun法の例 (赤い点が\((t,y(t))\)で、青い点が\((t+h,y(t+h))\)のHeun法による近似)
Heun法を拡散モデルのODEに適用すると以下のようになる。
\begin{align} \bar{y}_s^{(e)} &= \bar{y}_t + (\varsigma_s - \varsigma_t)\varepsilon(\bar{y}_t) \\ \bar{y}_s &= \bar{y}_t + \frac{\varsigma_s-\varsigma_t}{2}\left( \varepsilon(\bar{y}_t) + \varepsilon(\bar{y}_s^{(e)}) \right) \\ \end{align}
AUTOMATIC1111ではHeunという名前で実装されている。
- \(s<t\)
- \(h:=\varsigma_s-\varsigma_t\)
- \(\bar{y}_t\)が既に生成されていて、真の\(y_t\)との差が\(\bar{y}_t - y_t = \mathcal{O}(h^3)\)
- \(\varepsilon_\theta(y_t,t)\)が\(y_t\)に対してLipschitz連続
とする。
このとき、\(\bar{y}_s\)を次のように生成する。
\begin{align} \bar{y}_r &= Euler(\bar{y}_t, \varsigma_t\rightarrow\varsigma_r) \\ &= \bar{y}_t + (\varsigma_r - \varsigma_t)\varepsilon(\bar{y}_t) \\ \bar{y}_s &= \bar{y}_t + (\varsigma_s - \varsigma_t)\left( \varepsilon(\bar{y}_t)+\frac{1}{2k}(\varepsilon(\bar{y}_r)-\varepsilon(\bar{y}_t)) \right) \\ \end{align}
ただし、\(k\)は\(k\neq 0\)となる任意の実数であり、\(r:=\varsigma^{-1}(\varsigma_t+k(\varsigma_s-\varsigma_t))\)。
- \(s<t\)
- \(h:=\varsigma_s-\varsigma_t\)
- \(\bar{y}_t\)が既に生成されていて、真の\(y_t\)との差が\(\bar{y}_t - y_t = \mathcal{O}(h^3)\)
- \(\varepsilon_\theta(y_t,t)\)が\(y_t\)に対してLipschitz連続
とする。
このとき、\(\bar{y}_s\)を次のように生成する。
\begin{align} \bar{y}_s^{(e)} &= Euler(\bar{y}_t, \varsigma_t\rightarrow\varsigma_s) \\ &= \bar{y}_t + (\varsigma_s - \varsigma_t)\varepsilon(\bar{y}_t) \\ \bar{y}_s &= \bar{y}_t + \frac{\varsigma_s - \varsigma_t}{2}\left(\varepsilon(\bar{y}_t)+\varepsilon(\bar{y}_s^{(e)})\right) \\ \end{align}
LMS
LMS
一般にODEが以下の式で表されているとする。
\begin{align} \frac{dy}{dt} = f(y, t) \end{align}
このとき、
\begin{align} y(t_{i+1}) &= y(t_i) + \int_{t_i}^{t_{i+1}}\frac{dy}{dt}(t)dt \\ &= y(t_i) + \int_{t_i}^{t_{i+1}}f(y(t),t)dt \\ \end{align}
となる。
LMS(Linear Multistep, 線形多段法)では、既に計算済みの過去の値を用いて被積分関数である\(f(y(t),t)\)を多項式で近似することを試みる。
\(t_j\in\{t_i, t_{i-1}, \cdots , t_{i-p+1}\}\)の\(p\)点に対して、既に\(f(y(t_j),t_j)\)の近似値が求められているとする。計算済みの近似値を\(f_j\)と表す。
\(f(y(t),t)\)を近似する\(p-1\)次の多項式を\(P(t)\)と表す。
\(P(t_j)=f_j\)とならなければならないので、
\begin{align} P(t) &= f_i\frac{(t-t_{i-1})(t-t_{i-2})\cdots(t-t_{i-p+1})}{(t_i-t_{i-1})(t_i-t_{i-2})\cdots(t_i-t_{i-p+1})} + f_{i-1}\frac{(t-t_i)(t-t_{i-2})\cdots(t-t_{i-p+1})}{(t_{i-1}-t_i)(t_{i-1}-t_{i-2})\cdots(t_{i-1}-t_{i-k+1})} + \cdots + f_{i-p+1}\frac{(t-t_i)(t-t_{i-1})\cdots(t-t_{i-p+2})}{(t_{i-p+1}-t_i)(t_{i-p+1}-t_{i-1})\cdots(t_{i-p+1}-t_{i-p+2})} \\ &= f_i\prod_{\substack{m=0\\m\neq 0}}^{p-1}\frac{t-t_{i-m}}{t_i-t_{i-m}} + f_{i-1}\prod_{\substack{m=0\\m\neq 1}}^{p-1}\frac{t-t_{i-m}}{t_{i-1}-t_{i-m}} + \cdots + f_{i-p+1}\prod_{\substack{m=0\\m\neq p-1}}^{p-1}\frac{t-t_{i-m}}{t_{i-p+1}-t_{i-m}} \\ \end{align}
となる。
例えば\(f_j\)の項の分数部分は\(t=t_j\)以外のときに0になり、\(t=t_j\)のときに1になるように調整されている。
この多項式を最初の積分に代入する。
\begin{align} y(t_{i+1}) &= y(t_i) + \int_{t_i}^{t_{i+1}}f(y(t),t)dt \\ &\sim y(t_i) + \int_{t_i}^{t_{i+1}}P(t)dt \\ &= y(t_i) + \int_{t_i}^{t_{i+1}}\left( f_i\prod_{m\neq 0}\frac{t-t_{i-m}}{t_i-t_{i-m}} + f_{i-1}\prod_{m\neq 1}\frac{t-t_{i-m}}{t_{i-1}-t_{i-m}} + \cdots + f_{i-p+1}\prod_{m\neq p-1}\frac{t-t_{i-m}}{t_{i-p+1}-t_{i-m}} \right)dt \\ &= y(t_i) + f_i\int_{t_i}^{t_{i+1}}\prod_{m\neq 0}\frac{t-t_{i-m}}{t_i-t_{i-m}}dt + f_{i-1}\int_{t_i}^{t_{i+1}}\prod_{m\neq 1}\frac{t-t_{i-m}}{t_{i-1}-t_{i-m}}dt + \cdots + f_{i-p+1}\int_{t_i}^{t_{i+1}}\prod_{m\neq p-1}\frac{t-t_{i-m}}{t_{i-p+1}-t_{i-m}}dt \\ &=: y(t_i) + c_0f_i + c_1f_{i-1} + \cdots + c_{p-1}f_{i-p+1} \\ \end{align}
ここで、
\begin{align} c_j = \int_{t_i}^{t_{i+1}}\prod_{\substack{m=0\\m\neq j}}^{p-1}\frac{t-t_{i-m}}{t_{i-j}-t_{i-m}}dt \end{align}
このようにして\(y(t_{i+1})\)を求めることができた。このアルゴリズムをLMS(Linear Multistep)あるいはAdams–Bashforth法と呼ぶ。
\(t_j\)が等間隔の場合
特に\(t_j\)が等間隔、つまり全ての\(j\)に対して\(h=t_j-t_{j-1}\)となる場合のLMSを考える。
このとき、\(t_{i-j}-t_{i-m} = (m-j)h\)となる。
\(t=t_i+uh\)とすると、
\begin{align} c_j &= \int_{t_i}^{t_{i+1}}\prod_{m\neq j}\frac{t-t_{i-m}}{t_{i-j}-t_{i-m}}dt \\ &= \int_0^1\prod_{m\neq j}\frac{t_i+uh-t_{i-m}}{t_{i-j}-t_{i-m}}\frac{dt}{du}du \\ &= \int_0^1\prod_{m\neq j}\frac{mh+uh}{(m-j)h}hdu \\ &= h\int_0^1\prod_{m\neq j}\frac{m+u}{m-j}du \\ \end{align}
となる。
積分の中身は変数を含まない多項式なので、(計算に手間はかかるが)有理数の定数として求めることができる。
このことを利用して各\(k\)に対するLMSを導出する。(積分の具体的な計算過程は省略)
- \(p=1\)の場合 (Euler法と同じ)
\begin{align} y(t_{i+1}) &= y(t_i) + hf_i \\ \end{align}
- \(p=2\)の場合
\begin{align} y(t_{i+1}) &= y(t_i) + \frac{h}{2}\left( 3f_i - f_{i-1} \right) \\ \end{align}
- \(p=3\)の場合
\begin{align} y(t_{i+1}) &= y(t_i) + \frac{h}{12}\left( 23f_i - 16f_{i-1} + 5f_{i-2} \right) \\ \end{align}
- \(p=4\)の場合
\begin{align} y(t_{i+1}) &= y(t_i) + \frac{h}{24}\left( 55f_i - 59f_{i-1} + 37f_{i-2} - 9f_{i-3} \right) \\ \end{align}
より大きな\(p\)に対しても同様に求めることができる。
拡散モデルに適用
LMSを拡散モデルのODEに適用すると以下のようになる。
\begin{align} y_{t_{i+1}} = y_{t_i} + c_0\varepsilon_i + c_1\varepsilon_{i-1} + \cdots + c_{p-1}\varepsilon_{i-p+1} \\ \end{align}
ここで、
\begin{align} c_j = \int_{\varsigma_i}^{\varsigma_{i+1}}\prod_{\substack{m=0\\m\neq j}}^{p-1}\frac{s-\varsigma_{i-m}}{\varsigma_{i-j}-\varsigma_{i-m}}ds \end{align}
求めた\(y_{t_{i+1}}\)を用いて\(\varepsilon_{i+1}\)を計算・保持し、次の\(y_{t_{i+2}}\)を求めるために利用する。これを繰り返すことで\(y_{t_0}\)を得ることができる。
AUTOMATIC1111ではLMSという名前で実装されていて、\(p=4\)が採用されている。(最初の3ステップに限っては\(p=1, 2, 3\)で生成を始める)
- \(t_{i+1}<t_i<t_{i-1}<\cdots t_{i-p+1}\)
- \(\{\bar{y}_{t_{i-j}}\}_{j=0}^{p-1}\)が既に生成されている
- 既に計算済みの\(\{\varepsilon_{i-j}\}_{j=0}^{p-1} = \{\varepsilon(\bar{y}_{t_{i-j}})\}_{j=0}^{p-1}\)を保持している
とする。
このとき、\(\bar{y}_{t_{i+1}}\)を次のように生成する。
\begin{align} \bar{y}_{t_{i+1}} = \bar{y}_{t_i} + c_0\varepsilon_i + c_1\varepsilon_{i-1} + \cdots + c_{p-1}\varepsilon_{i-p+1} \\ \end{align}
ただし、
\begin{align} c_j := \int_{\varsigma_i}^{\varsigma_{i+1}}\prod_{\substack{m=0\\m\neq j}}^{p-1}\frac{s-\varsigma_{i-m}}{\varsigma_{i-j}-\varsigma_{i-m}}ds \end{align}
DEIS
拡散モデルのODEは
\begin{align} dy_t &= \varepsilon(y_t) d\varsigma_t \\ \end{align}
であるが、\(t\)の微分で表すと
\begin{align} dy_t &= \frac{d\varsigma_t}{dt} \varepsilon(y_t) dt \\ \end{align}
となる。したがって、\(y_{t_{i+1}}\)は以下のようになる。
\begin{align} y_{t_{i+1}} &= y_{t_i} + \int_{t_i}^{t_{i+1}} \frac{d\varsigma_t}{dt} \varepsilon(y_t) dt \\ \end{align}
拡散モデルのLMSでは\(\varepsilon(y_t)\)を\(\varsigma\)の多項式\(P(\varsigma)\)で近似していたが、今回は\(t\)の多項式\(P(t)\)で近似する。
既に計算済みの\(\{\varepsilon_{i-j}\}_{j=0}^{p-1} = \{\varepsilon(y_{t_{i-j}})\}_{j=0}^{p-1}\)があるとき、
\begin{align} y_{t_{i+1}} &= y_{t_i} + \int_{t_i}^{t_{i+1}} \frac{d\varsigma_t}{dt} \varepsilon(y_t) dt \\ &\sim y_{t_i} + \int_{t_i}^{t_{i+1}} \frac{d\varsigma_t}{dt} \left( \varepsilon_i\prod_{m\neq 0}\frac{t-t_{i-m}}{t_i-t_{i-m}} + \varepsilon_{i-1}\prod_{m\neq 1}\frac{t-t_{i-m}}{t_{i-1}-t_{i-m}} + \cdots + \varepsilon_{i-p+1}\prod_{m\neq p-1}\frac{t-t_{i-m}}{t_{i-p+1}-t_{i-m}} \right) dt \\ &= y_{t_i} + \left( \int_{t_i}^{t_{i+1}} \frac{d\varsigma_t}{dt} \prod_{m\neq 0}\frac{t-t_{i-m}}{t_i-t_{i-m}} dt \right) \varepsilon_i + \left( \int_{t_i}^{t_{i+1}} \frac{d\varsigma_t}{dt} \prod_{m\neq 1}\frac{t-t_{i-m}}{t_{i-1}-t_{i-m}} dt \right) \varepsilon_{i-1} + \cdots + \left( \int_{t_i}^{t_{i+1}} \frac{d\varsigma_t}{dt} \prod_{m\neq p-1}\frac{t-t_{i-m}}{t_{i-p+1}-t_{i-m}} dt \right) \varepsilon_{i-p+1} \\ &= y_{t_i} + c_0\varepsilon_i + c_1\varepsilon_{i-1} + \cdots + c_{p-1}\varepsilon_{i-p+1} \\ \end{align}
と近似することができる。
ここで、
\begin{align} c_j &:= \int_{t_i}^{t_{i+1}} \frac{d\varsigma_t}{dt} \prod_{m\neq j}\frac{t-t_{i-m}}{t_{i-j}-t_{i-m}} dt \end{align}
とするが、拡散モデルでは\(\alpha_t,\sigma_t\)かSDEの係数\(f(t),g(t)\)のいずれかが関数として与えられていることが前提となるので、\(\varsigma_t\)の微分も解析的に求めることができる。\(c_j\)自体を解析的に求めることができるとは限らないが、積分の中身を計算することができるので\(c_j\)は少なくとも数値的に求めることは可能である。
このアルゴリズムをDEIS(Diffusion Exponential Integrator Sampler)という。論文では上記のDEISを特にtAB-DEISと呼び、更に上で紹介したLMSをρAB-DEISと呼んでいる。ABはAdams-Bashforthを意味する。
(DEISの論文中で\(\Psi(s,t), L_t^{-T},\rho\)と表される値は、この投稿における\(\frac{\alpha_t}{\alpha_s}, \frac{1}{\sigma_t},\varsigma_t\)に相当する。)
- \(t_{i+1}<t_i<t_{i-1}<\cdots t_{i-p+1}\)
- \(\{\bar{y}_{t_{i-j}}\}_{j=0}^{p-1}\)が既に生成されている
- 既に計算済みの\(\{\varepsilon_{i-j}\}_{j=0}^{p-1} = \{\varepsilon(\bar{y}_{t_{i-j}})\}_{j=0}^{p-1}\)を保持している
とする。
このとき、\(\bar{y}_{t_{i+1}}\)を次のように生成する。
\begin{align} \bar{y}_{t_{i+1}} &= \bar{y}_{t_i} + c_0\varepsilon_i + c_1\varepsilon_{i-1} + \cdots + c_{p-1}\varepsilon_{i-p+1} \\ \end{align}
ただし、
\begin{align} c_j &:= \int_{t_i}^{t_{i+1}} \frac{d\varsigma_t}{dt} \prod_{m\neq j}\frac{t-t_{i-m}}{t_{i-j}-t_{i-m}} dt \end{align}
diffusersで実装されたDEISは\(\varepsilon(y_t)\)を\(t\)の多項式\(P(t)\)や\(\varsigma\)の多項式\(P(\varsigma)\)で近似するのではなく、\(\lambda=-\log\varsigma\)の多項式\(P(\lambda)\)で近似するアルゴリズムになっている模様。命名パターンに当てはめるならばλAB-DEISということになる。
PLMS
\(\varepsilon_\theta(x_t,t)\)の計算済みの値\(\{\varepsilon_{i-j}\}_{j=0}^{p-1}\)が既に求められているとき、この値が等間隔に並ぶような新たな時間軸\(s(\tau)\)を取る。つまり、\(s(jh) = t_i\)となるような関数\(s(\tau)\)を考える。
このとき、\(\varepsilon_{i-j}=\varepsilon(y_{s((i-j)h)},s((i-j)h))\)となり、\(\{\varepsilon_{i-j}\}_{j=0}^{p-1}\)は\(s\)の引数\(\tau\)に対して等間隔になる。
\(\tau\in(ih,(i+1)h)\)に対して、\(\varepsilon(y_{s(\tau)})\)を以下の積分で近似する。
\begin{align} \varepsilon(y_{s(\tau)}) &\sim \frac{1}{h}\int_{it}^{(i+1)h}\varepsilon(x_{s(\tau)},s(\tau))d\tau \\ \end{align}
更にLMSと同様に、積分の中の\(\varepsilon(x_{s(\tau)},s(\tau))\)を過去の値を用いた\(\tau\)の多項式で近似する。
\begin{align} \varepsilon(x_{s(\tau)},s(\tau)) &\sim P(\tau) \\ &= \varepsilon_i\prod_{m\neq 0}\frac{\tau-(i-m)h}{ih-(i-m)h} + \varepsilon_{i-1}\prod_{m\neq 1}\frac{\tau-(i-m)h}{(i-1)h-(i-m)h} + \cdots + \varepsilon_{i-p+1}\prod_{m\neq p-1}\frac{\tau-(i-m)h}{(i-p+1)h-(i-m)h} \\ \end{align}
積分に戻す。
\begin{align} \varepsilon(y_{s(\tau)}) &\sim \frac{1}{h}\int_{it}^{(i+1)h}\varepsilon(x_{s(\tau)},s(\tau))d\tau \\ &\sim \frac{1}{h}\int_{it}^{(i+1)h}\left( \varepsilon_i\prod_{m\neq 0}\frac{\tau-(i-m)h}{ih-(i-m)h} + \varepsilon_{i-1}\prod_{m\neq 1}\frac{\tau-(i-m)h}{(i-1)h-(i-m)h} + \cdots + \varepsilon_{i-p+1}\prod_{m\neq p-1}\frac{\tau-(i-m)h}{(i-p+1)h-(i-m)h} \right)d\tau \\ &= \frac{c_0}{h}\varepsilon_i + \frac{c_1}{h}\varepsilon_{i-1} + \cdots + \frac{c_{p-1}}{h}\varepsilon_{i-p+1} \\ &= a_0\varepsilon_i + a_1\varepsilon_{i-1} + \cdots + a_{p-1}\varepsilon_{i-p+1} \\ \end{align}
ここで\(a_j\)は、\(\tau\)が等間隔であることから以下の定数になる。
\begin{align} a_j &= \frac{c_j}{h} \\ &= \int_0^1\prod_{\substack{m=0\\m\neq j}}^{p-1}\frac{m+u}{m-j}du \end{align}
PLMS(Pseudo Linear Multistep)では、このように近似された\(\varepsilon(y_{s(\tau)})\)を用いて以下のように\(\bar{y}_s\)を生成する。
\begin{align} \bar{y}_s &= \bar{y}_t + (\varsigma_s-\varsigma_t)\varepsilon(y_{s(\tau)}) \\ &= \bar{y}_t + (\varsigma_s-\varsigma_t)\left(a_0\varepsilon_i + a_1\varepsilon_{i-1} + \cdots + a_{p-1}\varepsilon_{i-p+1}\right) \\ \end{align}
AUTOMATIC1111ではPLMSという名前で、\(p=4\)のものが実装されている。(最初の3ステップに限っては\(p=1,2,3\)で生成を始める)
\begin{align} \bar{y}_s = \bar{y}_t + (\varsigma_s-\varsigma_t)\frac{1}{24}\left( 55\varepsilon_i - 59\varepsilon_{i-1} + 37\varepsilon_{i-2} - 9\varepsilon_{i-3} \right) \end{align}
- \(t_{i+1}<t_i<t_{i-1}<\cdots t_{i-p+1}\)
- \(\{\bar{y}_{t_{i-j}}\}_{j=0}^{p-1}\)が既に生成されている
- 既に計算済みの\(\{\varepsilon_{i-j}\}_{j=0}^{p-1} = \{\varepsilon(\bar{y}_{t_{i-j}})\}_{j=0}^{p-1}\)を保持している
とする。
このとき、\(\bar{y}_{t_{i+1}}\)を次のように生成する。
\begin{align} \bar{y}_{t_{i+1}} &= \bar{y}_t + (\varsigma_s-\varsigma_t)\left(a_0\varepsilon_i + a_1\varepsilon_{i-1} + \cdots + a_{p-1}\varepsilon_{i-p+1}\right) \\ \end{align}
ただし、
\begin{align} a_j = \int_0^1\prod_{\substack{m=0\\m\neq j}}^{p-1}\frac{m+u}{m-j}du \end{align}
参考
- [2204.13902] Fast Sampling of Diffusion Models with Exponential Integrator
- [2202.09778] Pseudo Numerical Methods for Diffusion Models on Manifolds
- [2206.00364] Elucidating the Design Space of Diffusion-Based Generative Models
- 微分方程式の数値解法 - 東京大学工学部 精密工学科 プログラミング応用 I・II
- 多段階解法 (東京都立大学)
- さんぷらーについて - 勾配降下党青年局