この記事では拡散モデルの生成過程で使われるサンプラーと呼ばれる様々なアルゴリズムを解説する。
前回同様に、SMLDの前提で話を進める。表記についても前回記事と同じものを用いる。

関連記事

• DDPM: Denoising Diffusion Probabilistic Models
• DDPMの関連技術
• Stable Diffusionのモデル構造
• 拡散モデルの確率微分方程式
• 拡散モデルのサンプラー (1) - 離散過程・古典的数値計算法・LMS
• 拡散モデルのサンプラー (2) - DPM-Solver (本記事)
• 拡散モデルのサンプラー (3) - UniPC
• 拡散モデルのサンプラー - まとめ・Timestep Scheduler

目次

• DPM-Solver
  • 理論
  • DPM-Solver-1
  • DPM-Solver-2
  • DPM-Solver-3
• DPM-Solver++
  • 理論
  • DPM-Solver++
  • DPM-Solver++(2S)
  • DPM-Solver++(2M)
• SDE-DPM-Solver
  • 理論
  • SDE-DPM-Solver-1
  • SDE-DPM-Solver-2M
• SDE-DPM-Solver++
  • 理論
  • SDE-DPM-Solver++1
  • SDE-DPM-Solver++(2M)
• 参考

DPM-Solver

理論

積分方程式

以前の考察によると、\(y_t\)に関するODEは以下のように表される。

\begin{align} dy_t &= -\sigma_t\nabla\log p_t(x_t)d\varsigma_t \\ &\sim \varepsilon(y_t)d\varsigma_t \\ \end{align}

ここで、

\begin{align} \lambda_t &:= \frac{1}{2}\log SNR(t) \\ &= \log \frac{\alpha_t}{\sigma_t} \\ &= -\log \varsigma_t \\ \end{align}

という新たな変数を導入する。
\(h:=\lambda_s-\lambda_t\)とすると、

\begin{align} \varsigma_t = e^{-\lambda_t} \\ \end{align}

\begin{align} e^h &= e^{\lambda_s-\lambda_t} \\ &= \frac{\varsigma_t}{\varsigma_s} \\ \end{align}

\begin{align} \varsigma_s-\varsigma_t &= \varsigma_s(1-e^h) \\ &= \mathcal{O}(h) \end{align}

が成り立つ。
\(\varepsilon, x_t\)を以下のように\(\lambda\)の式に書き換える。(\(\lambda^{-1}\)は\(\lambda_t\)の逆関数)

\begin{align} \hat{y}_\lambda &:= y_{\lambda^{-1}(\lambda)} \\ \hat{\varepsilon}(\lambda) &:= \varepsilon(\hat{y}_\lambda, {\lambda^{-1}(\lambda)}) \\ &= \varepsilon_\theta\left(x_{\lambda^{-1}(\lambda)}, \lambda^{-1}(\lambda)\right) \\ \end{align}

ODEは以下のようになる。

\begin{align} dy_t &= \varepsilon(y_t)d\varsigma_t \\ &= \hat{\varepsilon}(\hat{y}_{\lambda_t},\lambda^{-1}(\lambda_t))\frac{d\varsigma_t}{d\lambda_t}d\lambda_t \\ &= \hat{\varepsilon}(\lambda_t)\frac{de^{-\lambda_t}}{d\lambda_t}d\lambda_t \\ &= -e^{-\lambda_t}\hat{\varepsilon}(\lambda_t)d\lambda_t \\ \end{align}

したがって、ODEから以下の積分方程式を導くことができる。
このような形に式を変形して問題を解く手法をExponential integratorという。

\begin{align} y_s = y_t - \int_{\lambda_t}^{\lambda_s} e^{-\lambda}\hat{\varepsilon}(\lambda)d\lambda \\ \end{align}

積分の中の\(\hat{\varepsilon}\)は未知の\(y\)に依存しているので、このままでは計算することができない。
\(\hat{\varepsilon}(\lambda)\)を何とかして近似することがDPM-Solverの目的となる。

Taylor展開

\(\hat{\varepsilon}(\lambda)\)をTaylor展開する。

\begin{align} \hat{\varepsilon}(\lambda) = \sum_{n=0}^{p-1} \frac{(\lambda-\lambda_t)^n}{n!}\hat{\varepsilon}^{(n)}(\lambda_t) + \mathcal{O}\left(|\lambda-\lambda_t|^p\right) \\ \end{align}

この式を積分方程式に代入。

\begin{align} y_s &= y_t - \int_{\lambda_t}^{\lambda_s} e^{-\lambda}\left( \sum_{n=0}^{p-1} \frac{(\lambda-\lambda_t)^n}{n!}\hat{\varepsilon}^{(n)}(\lambda_t) + \mathcal{O}\left(|\lambda-\lambda_t|^p\right) \right)d\lambda \\ &= y_t - \sum_{n=0}^{p-1} \hat{\varepsilon}^{(n)}(\lambda_t) \int_{\lambda_t}^{\lambda_s} e^{-\lambda} \frac{(\lambda-\lambda_t)^n}{n!}d\lambda + \int_{\lambda_t}^{\lambda_s} e^{-\lambda} \mathcal{O}\left(|\lambda-\lambda_t|^p\right)d\lambda \\ \end{align}

ここで、\(h:=\lambda_s-\lambda_t, \delta:=\frac{\lambda-\lambda_t}{h}\)として積分を計算する、

\begin{align} \int_{\lambda_t}^{\lambda_s} e^{-\lambda} \frac{(\lambda-\lambda_t)^n}{n!}d\lambda &= \int_0^1 e^{-h\delta-\lambda_t} \frac{(h\delta)^n}{n!}hd\delta \\ &= e^{-\lambda_s}h^{n+1}\int_0^1 e^{h(1-\delta)} \frac{\delta^n}{n!}d\delta \\ &= \varsigma_sh^{n+1}\int_0^1 e^{h(1-\delta)} \frac{\delta^n}{n!}d\delta \\ &=: \varsigma_sh^{n+1}\phi_{n+1}(h) \\ \end{align}

\(\phi_n(h)\)は逐次的に以下のように求めることができる。

\begin{align} \phi_n(h) &= \int_0^1 e^{h(1-\delta)} \frac{\delta^{n-1}}{(n-1)!}d\delta \\ &= \left[ -\frac{1}{h}e^{h(1-\delta)}\frac{\delta^{n-1}}{(n-1)!} \right]_0^1 + \frac{1}{h}\int_0^1 e^{h(1-\delta)} \frac{\delta^{n-2}}{(n-2)!}d\delta \\ &= -\frac{1}{h}\frac{1}{(n-1)!} + \frac{1}{h}\phi_{n-1}(h) \\ &= -\frac{1}{h}\frac{1}{(n-1)!} + \frac{1}{h}\left( -\frac{1}{h}\frac{1}{(n-2)!} + \frac{1}{h}\phi_{n-2}(h) \right) \\ &= -\frac{1}{h}\frac{1}{(n-1)!} - \frac{1}{h^2}\frac{1}{(n-2)!} + \frac{1}{h^2}\phi_{n-2}(h) \\ &\quad \vdots \\ &= -\frac{1}{h}\frac{1}{(n-1)!} - \frac{1}{h^2}\frac{1}{(n-2)!} - \cdots - \frac{1}{h^{n-1}}\frac{1}{1!} + \frac{1}{h^{n-1}}\phi_1(h) \\ &= -\sum_{m=1}^{n-1}\frac{1}{h^{n-m}}\frac{1}{m!} + \frac{1}{h^{n-1}}\int_0^1 e^{h(1-\delta)} \frac{\delta^0}{0!}d\delta \\ &= -\sum_{m=1}^{n-1}\frac{1}{h^{n-m}}\frac{1}{m!} - \frac{1}{h^{n-1}}\frac{1}{h}\left( 1-e^h \right) \\ &= -\sum_{m=0}^{n-1}\frac{1}{h^{n-m}}\frac{1}{m!} + \frac{e^h}{h^n} \\ &= \frac{1}{h^n}\left( e^h - \sum_{m=0}^{n-1}\frac{h^m}{m!} \right) \\ &= \frac{1}{h^n}\sum_{m=n}^\infty\frac{h^m}{m!} \\ &= \sum_{m=0}^\infty\frac{h^m}{(n+m)!} \\ \end{align}

\(e^h\)のTaylor展開と照らし合わせると、各\(\phi_n(h)\)は次のように表すことができ、全て\(\mathcal{O}(1)\)のオーダーであることがわかる。

\begin{align} \phi_1(h) &= \frac{1}{h^1}\left( e^h - \sum_{m=0}^{0}\frac{h^m}{m!} \right) = \frac{1}{1!} + \frac{h}{2!} + \frac{h^2}{3!} + \frac{h^3}{4!} + \cdots \\ \phi_2(h) &= \frac{1}{h^2}\left( e^h - \sum_{m=0}^{1}\frac{h^m}{m!} \right) = \frac{1}{2!} + \frac{h}{3!} + \frac{h^2}{4!} + \frac{h^3}{5!} + \cdots \\ \phi_3(h) &= \frac{1}{h^3}\left( e^h - \sum_{m=0}^{2}\frac{h^m}{m!} \right) = \frac{1}{3!} + \frac{h}{4!} + \frac{h^2}{5!} + \frac{h^3}{6!} + \cdots \\ \vdots \end{align}

積分方程式に戻って以下の結果を得る。

\begin{align} y_s &= y_t - \sum_{n=0}^{p-1} \hat{\varepsilon}^{(n)}(\lambda_t) \int_{\lambda_t}^{\lambda_s} e^{-\lambda} \frac{(\lambda-\lambda_t)^n}{n!}d\lambda + \int_{\lambda_t}^{\lambda_s} e^{-\lambda} \mathcal{O}\left(|\lambda-\lambda_t|^p\right)d\lambda \\ &= y_t - \sum_{n=0}^{p-1} \hat{\varepsilon}^{(n)}(\lambda_t)\varsigma_sh^{n+1}\phi_{n+1}(h) + \mathcal{O}\left(h^{p+1}\right) \\ &= y_t - \varsigma_s\sum_{n=1}^{p} h^n\phi_n(h)\hat{\varepsilon}^{(n-1)}(\lambda_t) + \mathcal{O}\left(h^{p+1}\right) \\ \end{align}

DPM-Solver-1

DPM-Solver-1では\(p=1\)までの項を計算する。(収束次数は1)
\(\hat{\varepsilon}\)の微分が現れないのでそのまま導くことができる。\(\bar{y}_t-y_t=\mathcal{O}(h^2)\)とすると、

\begin{align} y_s &= y_t - \varsigma_s\sum_{n=1}^{1} h^n\phi_n(h)\hat{\varepsilon}^{(n-1)}(\lambda_t) + \mathcal{O}(h^2) \\ &= y_t - \varsigma_s h^1\phi_1(h)\hat{\varepsilon}^{(0)}(\lambda_t) + \mathcal{O}(h^2) \\ &= y_t - \varsigma_s h\frac{e^h-1}{h}\hat{\varepsilon}(\lambda_t) + \mathcal{O}(h^2) \\ &= y_t - \varsigma_s \left( \frac{\varsigma_t}{\varsigma_s}-1 \right)\varepsilon(y_t) + \mathcal{O}(h^2) \\ &= y_t + \left( \varsigma_s - \varsigma_t \right)\varepsilon(y_t) + \mathcal{O}(h^2) \\ &= \bar{y}_t + \left( \varsigma_s - \varsigma_t \right)\varepsilon(\bar{y}_t) + \mathcal{O}(h^2) \\ \end{align}

したがって、近似値\(\bar{y}_s\)を次のように定める。

\begin{align} \bar{y}_s &= \bar{y}_t + \left( \varsigma_s - \varsigma_t \right)\varepsilon(\bar{y}_t) \end{align}

これはEuler法と全く同じアルゴリズムである。

DPM-Solver-2

DPM-Solver-2では\(p=2\)までの項を計算する。(収束次数は2)

\begin{align} \bar{y}_s &= \bar{y}_t - \varsigma_s\sum_{n=1}^{2} h^n\phi_n(h)\hat{\varepsilon}^{(n-1)}(\lambda_t) + \mathcal{O}(h^3) \\ &= \bar{y}_t - \varsigma_s\left( (e^h-1)\hat{\varepsilon}(\lambda_t) + (e^h-h-1)\hat{\varepsilon}^{(1)}(\hat{y}_{\lambda_t},\lambda_t) \right) + \mathcal{O}(h^3) \\ &= \bar{y}_t - \varsigma_s\left( (e^h-1)\varepsilon(y_t) + \left(\frac{h(e^h-1)}{2} + \mathcal{O}(h^3)\right)\hat{\varepsilon}^{(1)}(\lambda_t) \right) + \mathcal{O}(h^3) \\ &= \bar{y}_t - \varsigma_s\left( (e^h-1)\varepsilon(y_t) + \frac{h(e^h-1)}{2}\hat{\varepsilon}^{(1)}(\lambda_t) \right) + \mathcal{O}(h^3) \\ &= \bar{y}_t - \varsigma_s(e^h-1)\left( \varepsilon(y_t) + \frac{h}{2}\hat{\varepsilon}^{(1)}(\lambda_t) \right) + \mathcal{O}(h^3) \\ &= \bar{y}_t + (\varsigma_s-\varsigma_t)\left( \varepsilon(y_t) + \frac{h}{2}\hat{\varepsilon}^{(1)}(\lambda_t) \right) + \mathcal{O}(h^3) \\ \end{align}

(Heun法の導出過程と同様に)\(k\neq 0\)を取り、以下のように\(\lambda_r,\varsigma_r,r\)を定義する。

\begin{align} \begin{cases} \lambda_r &:= \lambda_t + kh \\ &= (1-k)\lambda_t + k\lambda_s \\ \varsigma_r &:= e^{-\lambda_r} \\ &= \varsigma_t^{1-k}\varsigma_s^{k} \\ r &:= \lambda^{-1}(\lambda_r) \\ \end{cases} \end{align}

ステップ幅\(kh\)のDPM-Solver-1 (Euler法)で生成した値\(\bar{y}_r=\bar{y}_{\lambda^{-1}(\lambda_t+kh)}\)を用いて、\(\hat{\varepsilon}^{(1)}(\lambda_t)\)を次のように表す。(\(\hat{\varepsilon}\)にLipschitz連続性を仮定する必要がある)

\begin{align} kh\hat{\varepsilon}^{(1)}(\lambda_t) &= \hat{\varepsilon}(\lambda_t+kh) - \hat{\varepsilon}(\lambda_t) + \mathcal{O}(h^2) \\ &= \varepsilon(y_r) - \varepsilon(y_t) + \mathcal{O}(h^2) \\ &= \varepsilon(\bar{y}_r) + \mathcal{O}(|\bar{y}_r-y_r|) - \varepsilon(y_t) + \mathcal{O}(h^2) \\ &= \varepsilon(\bar{y}_r) + \mathcal{O}((kh)^2) - \varepsilon(y_t) + \mathcal{O}(h^2) \\ &= \varepsilon(\bar{y}_r) - \varepsilon(y_t) + \mathcal{O}(h^2) \\ \end{align}

元の式に戻す。\(\bar{y}_t-y_t=\mathcal{O}(h^3)\)とすると、\(s_t\)を以下のように2次Runge-Kutta法によく似た形で近似できる。
(\(\varsigma_s-\varsigma_t=\mathcal{O}(h)\)であることを利用)

\begin{align} y_s &= y_t + (\varsigma_s-\varsigma_t)\left( \varepsilon(y_t) + \frac{h}{2}\hat{\varepsilon}^{(1)}(\hat{y}_{\lambda_t},\lambda_t) \right) + \mathcal{O}(h^3) \\ &= y_t + (\varsigma_s-\varsigma_t)\left( \varepsilon(y_t) + \frac{1}{2k}\left( \varepsilon(\bar{y}_r) - \varepsilon(y_t) \right) + \mathcal{O}(h^2) \right) + \mathcal{O}(h^3) \\ &= y_t + (\varsigma_s-\varsigma_t)\left( \left(1-\frac{1}{2k}\right)\varepsilon(y_t) + \frac{1}{2k}\varepsilon(\bar{y}_r) \right) + \mathcal{O}(h^3) \\ &= \bar{y}_t + (\varsigma_s-\varsigma_t)\left( \left(1-\frac{1}{2k}\right)\varepsilon(\bar{y}_t) + \frac{1}{2k}\varepsilon(\bar{y}_r) \right) + \mathcal{O}(h^3) \\ \end{align}

したがって、近似値\(\bar{y}_s\)を次のように定める。

\begin{align} \bar{y}_s &= \bar{y}_t + (\varsigma_s-\varsigma_t)\left( \left(1-\frac{1}{2k}\right)\varepsilon(\bar{y}_t) + \frac{1}{2k}\varepsilon(\bar{y}_r) \right) \end{align}

\(\bar{y}_r\)はDPM-Solver-1によって生成するので、以下のようになる。

\begin{align} \bar{y}_r &= \bar{y}_t + (\varsigma_r-\varsigma_t)\varepsilon(y_t) \\ &= \bar{y}_t + (\varsigma_t^{1-k_1}\varsigma_s^{k_1}-\varsigma_t)\varepsilon(\bar{y}_t) \\ \end{align}

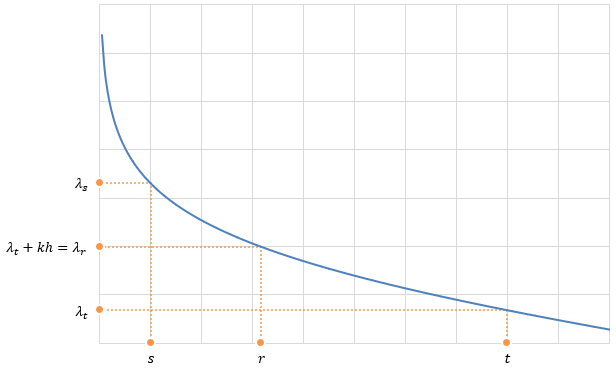
タイムステップ\(t\)と\(\lambda_t\)の関係

DPM-Solver-2では特に\(k_1=1/2\)としている。

\begin{align} \bar{y}_r &= \bar{y}_t + (\sqrt{\varsigma_t\varsigma_s}-\varsigma_t)\varepsilon(\bar{y}_t) \\ \bar{y}_s &= \bar{y}_t + (\varsigma_s-\varsigma_t)\varepsilon(\bar{y}_r) \\ \end{align}

AUTOMATIC1111ではDPM2という名前で実装されている。

DPM-Solver-3

DPM-Solver-3では\(p=3\)までの項を計算する。(収束次数は3)

1次の近似

\(k_1\neq 0\)を取り、\(r_1:=\lambda^{-1}(\lambda_t+k_1h)\)とする。
\(\bar{y}_{r_1}\)をDPM-Solver-1で次のように求める。

\begin{align} \bar{y}_{r_1} &= \bar{y}_t + (\varsigma_{r_1} - \varsigma_t)\varepsilon(\bar{y}_t) \\ \end{align}

このとき以下の近似が成り立つ。

\begin{align} k_1h\hat{\varepsilon}^{(1)}(\hat{y}_{\lambda_t}) &= \hat{\varepsilon}(\lambda_t+k_1h) - \hat{\varepsilon}(\lambda_t) + \mathcal{O}(h^2) \\ &= \varepsilon(y_{r_1}) - \varepsilon(y_t) + \mathcal{O}(h^2) \\ &= \varepsilon(\bar{y}_{r_1}) + \mathcal{O}(|y_{r_1}-\bar{y}_1|) - \varepsilon(y_t) + \mathcal{O}(h^2) \\ &= \varepsilon(\bar{y}_{r_1}) + \mathcal{O}(h^2) - \varepsilon(y_t) + \mathcal{O}(h^2) \\ &= \varepsilon(\bar{y}_{r_1}) - \varepsilon(y_t) + \mathcal{O}(h^2) \\ \end{align}

2次の近似

\(k_2\neq 0\)を取り、\(r_2:=\lambda^{-1}(\lambda_t+k_2h)\)とする。
\(\bar{y}_t-y_t=\mathcal{O}(h^3)\)とすると、\(\hat{\varepsilon}\)のTaylor展開を用いて\(y_{r_2}\)を次のように近似できる。

\begin{align} y_{r_2} &= y_t - \varsigma_{r_2}\left( k_2h\phi_1(k_2h)\hat{\varepsilon}^{(0)}(\lambda_t) + (k_2h)^2\phi_2(k_2h)\hat{\varepsilon}^{(1)}(\lambda_t) \right) + \mathcal{O}(h^3) \\ &= y_t - \varsigma_{r_2}\left( k_2h\phi_1(k_2h)\varepsilon(y_t) + \frac{k_2^2h}{k_1}\phi_2(k_2h)k_1h\hat{\varepsilon}^{(1)}(\lambda_t) \right) + \mathcal{O}(h^3) \\ &= y_t - \varsigma_{r_2}\left( k_2h\phi_1(k_2h)\varepsilon(y_t) + \frac{k_2^2h}{k_1}\phi_2(k_2h)\left( \varepsilon(\bar{y}_{r_1}) - \varepsilon(y_t) + \mathcal{O}(h^2) \right) \right) + \mathcal{O}(h^3) \\ &= \bar{y}_t + \mathcal{O}(h^3) - \varsigma_{r_2}\left( k_2h\phi_1(k_2h)\left(\varepsilon(\bar{y}_t)+\mathcal{O}(h^2)\right) + \frac{k_2^2h}{k_1}\phi_2(k_2h)\left( \varepsilon(\bar{y}_{r_1}) - \varepsilon(\bar{y}_t)+\mathcal{O}(h^2) \right) \right) + \mathcal{O}(h^3) \\ &= \bar{y}_t - \varsigma_{r_2}\left( k_2h\phi_1(k_2h)\varepsilon(\bar{y}_t) + \frac{k_2^2h}{k_1}\phi_2(k_2h)\left( \varepsilon(\bar{y}_{r_1}) - \varepsilon(\bar{y}_t) \right) \right) + \mathcal{O}(h^3) \\ \end{align}

ここで、近似値\(\bar{y}_{r_2}\)を次のように定めると、\(y_{r_2}-\bar{y}_{r_2}=\mathcal{O}(h^3)\)となる。

\begin{align} \bar{y}_{r_2} &= \bar{y}_t - \varsigma_{r_2}\left( k_2h\phi_1(k_2h)\varepsilon(\bar{y}_t) + \frac{k_2^2h}{k_1}\phi_2(k_2h)\left( \varepsilon(\bar{y}_{r_1}) - \varepsilon(\bar{y}_t) \right) \right) \end{align}

このとき以下の近似が成り立つ。

\begin{align} k_2h\hat{\varepsilon}^{(1)}(\lambda_t) + \frac{(k_2h)^2}{2}\hat{\varepsilon}^{(2)}(\lambda_t) &= \hat{\varepsilon}(\lambda_t+k_2h) - \hat{\varepsilon}(\lambda_t) + \mathcal{O}(h^3) \\ &= \varepsilon(y_{r_2}) - \varepsilon(y_t) + \mathcal{O}(h^3) \\ &= \varepsilon(\bar{y}_{r_2}) + \mathcal{O}(|y_{r_2}-\bar{y}_{r_2}|) - \varepsilon(y_t) + \mathcal{O}(h^3) \\ &= \varepsilon(\bar{y}_{r_2}) + \mathcal{O}(h^3) - \varepsilon(y_t) + \mathcal{O}(h^3) \\ &= \varepsilon(\bar{y}_{r_2}) - \varepsilon(y_t) + \mathcal{O}(h^3) \\ \end{align}

3次の近似

\(\bar{y}_t-y_t=\mathcal{O}(h^4)\)とすると、\(y_s\)を次のように近似できる。

\begin{align} y_s &= y_t - \varsigma_s\left( h\phi_1(h)\hat{\varepsilon}^{(0)}(y_t) + h^2\phi_2(h)\hat{\varepsilon}^{(1)}(\lambda_t) + h^3\phi_3(h)\hat{\varepsilon}^{(2)}(\lambda_t) \right) + \mathcal{O}(h^4) \\ &= y_t - \varsigma_s\left( h\phi_1(h)\varepsilon(y_t) + \frac{h}{k_2}\phi_2(h)k_2h\hat{\varepsilon}^{(1)}(\lambda_t) + h^3\phi_3(h)\hat{\varepsilon}^{(2)}(\lambda_t) \right) + \mathcal{O}(h^4) \\ &= y_t - \varsigma_s\left( h\phi_1(h)\varepsilon(y_t) + \frac{h}{k_2}\phi_2(h)\left( \varepsilon(\bar{y}_{r_2}) - \varepsilon(y_t) - \frac{(k_2h)^2}{2}\hat{\varepsilon}^{(2)}(\lambda_t) + \mathcal{O}(h^3) \right) + h^3\phi_3(h)\hat{\varepsilon}^{(2)}(\lambda_t) \right) + \mathcal{O}(h^4) \\ &= y_t - \varsigma_s\left( h\phi_1(h)\varepsilon(y_t) + \frac{h}{k_2}\phi_2(h)\left( \varepsilon(\bar{y}_{r_2}) - \varepsilon(y_t) \right) + h^3\left( \phi_3(h) - \frac{k_2}{2}\phi_2(h) \right)\hat{\varepsilon}^{(2)}(\lambda_t) \right) + \mathcal{O}(h^4) \\ &= \bar{y}_t - \varsigma_s\left( h\phi_1(h)\varepsilon(\bar{y}_t) + \frac{h}{k_2}\phi_2(h)\left( \varepsilon(\bar{y}_{r_2}) - \varepsilon(\bar{y}_t) \right) + h^3\left( \phi_3(h) - \frac{k_2}{2}\phi_2(h) \right)\hat{\varepsilon}^{(2)}(\lambda_t) \right) + \mathcal{O}(h^4) \\ \end{align}

ここで、計算不可能な\(\hat{\varepsilon}^{(2)}\)の項は、\(k_2\)を調整して係数を\(\mathcal{O}(h^4)\)のオーダーにすることで式から抹消する。

\begin{align} h^3\left( \phi_3(h) - \frac{k_2}{2}\phi_2(h) \right) &= h^3\left( \frac{1}{6} + \mathcal{O}(h) - \frac{k_2}{2}\left( \frac{1}{2} + \mathcal{O}(h) \right) \right) \\ &= h^3\left( \frac{1}{6} - \frac{k_2}{4} \right) + \mathcal{O}(h^4) \\ &= \frac{h^3}{4}\left( \frac{2}{3} - k_2 \right) + \mathcal{O}(h^4) \\ \end{align}

\(k_2=2/3\)とすると良いことがわかる。
したがって、近似値\(\bar{y}_s\)を次のように定める。

\begin{align} \bar{y}_s &= \bar{y}_t - \varsigma_s\left( h\phi_1(h)\varepsilon(\bar{y}_t) + \frac{h}{k_2}\phi_2(h)\left( \varepsilon(\bar{y}_{r_2}) - \varepsilon(\bar{y}_t) \right) + h^3\left( \phi_3(h) - \frac{k_2}{2}\phi_2(h) \right)\hat{\varepsilon}^{(2)}(\lambda_t) \right) \\ &= y_t - \varsigma_s\left( h\phi_1(h)\varepsilon(\bar{y}_t) + \frac{h}{k_2}\phi_2(h)\left( \varepsilon(\bar{y}_{r_2}) - \varepsilon(\bar{y}_t) \right) \right) \\ \end{align}

DPM-Solver++

理論

データ予測モデル

DPM-Solver++では、予測したノイズ\(\varepsilon(y_t)\)を利用するのではなく、各タイムステップにおける生成データ\(x_0\)の予測値

\begin{align} x_\theta(x_t,t) &:= \frac{x_t - \sigma_t\varepsilon_\theta(x_t,t)}{\alpha_t} \\ &= y_t - \varsigma_t\varepsilon(y_t) \\ \end{align}

の形に変換して利用する。ノイズを利用するモデルをノイズ予測モデルと呼ぶのに対して、DPM-Solver++のようにデータを予測するモデルをデータ予測モデルと呼ぶ。

データ予測モデルでも\(\varepsilon\)のときと同様に\(x_\theta(y_t,t), x_\theta(y_t), \hat{x}_\theta(\lambda)\)といった表記を用いる。

積分方程式

ODEをデータ予測モデルの形式に書き換える。

\begin{align} dy_t &= \varepsilon(y_t)d\varsigma_t \\ &= \frac{x_t-\alpha_tx_\theta(y_t)}{\sigma_t}\frac{d\varsigma_t}{d\lambda_t}d\lambda_t \\ &= -\frac{\alpha_ty_t-\alpha_tx_\theta(y_t)}{\sigma_t}\varsigma_t d\lambda_t \\ &= -\frac{y_t-x_\theta(y_t)}{\varsigma_t}\varsigma d\lambda_t \\ &= \left(-y_t+x_\theta(y_t)\right)d\lambda_t \\ \end{align}

\(\frac{y_t}{\varsigma_t}\)の微分を考える。

\begin{align} d\frac{y_t}{\varsigma_t} &= d\left( y_te^{\lambda_t} \right) \\ &= y_te^{\lambda_t}d\lambda_t + dy_te^{\lambda_t} \\ &= e^{\lambda_t}\left( y_td\lambda_t + dy_t \right) \\ &= e^{\lambda_t}\left( y_t -y_t+x_\theta(y_t) \right)d\lambda_t \\ &= e^{\lambda_t}x_\theta(y_t)d\lambda_t \\ &= e^{\lambda_t}\hat{x}_\theta(\lambda_t)d\lambda_t \\ \end{align}

よってデータ予測モデルの積分方程式は以下のようになる。

\begin{align} \frac{y_s}{\varsigma_s} &= \frac{y_t}{\varsigma_t} + \int_{\lambda_s}^{\lambda_t} e^\lambda\hat{x}_\theta(\lambda)d\lambda \\ \end{align}

\begin{align} y_s &= \frac{\varsigma_s}{\varsigma_t}y_t + \varsigma_s\int_{\lambda_s}^{\lambda_t} e^\lambda\hat{x}_\theta(\lambda)d\lambda \\ \end{align}

Taylor展開

積分の中の\(\hat{x}_\theta(\lambda)\)をTaylor展開する。

\begin{align} y_s &= \frac{\varsigma_s}{\varsigma_t}y_t + \varsigma_s\int_{\lambda_s}^{\lambda_t} e^\lambda\hat{x}_\theta(\lambda)d\lambda \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + \varsigma_s\int_{\lambda_s}^{\lambda_t} e^\lambda\left( \sum_{n=0}^{p-1}\frac{(\lambda-\lambda_t)^n}{n!}\hat{x}_\theta^{(n)}(\lambda_t) + \mathcal{O}(|\lambda-\lambda_t|^p) \right)d\lambda \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + \varsigma_s\sum_{n=0}^{p-1}\hat{x}_\theta^{(n)}(\lambda_t)\int_{\lambda_s}^{\lambda_t} e^\lambda\frac{(\lambda-\lambda_t)^n}{n!}d\lambda + \varsigma_s\int_{\lambda_s}^{\lambda_t}e^\lambda\mathcal{O}(|\lambda-\lambda_t|^p)d\lambda \\ \end{align}

\(h:=\lambda_s-\lambda_t, \delta:=\frac{\lambda-\lambda_t}{\lambda_s-\lambda_t}\)として積分を計算。

\begin{align} \int_{\lambda_s}^{\lambda_t} e^\lambda\frac{(\lambda-\lambda_t)^n}{n!}d\lambda &= \int_0^1 e^{\lambda_t+h\delta}\frac{(h\delta)^n}{n!}hd\delta \\ &= e^{\lambda_s}h^{n+1}\int_0^1 e^{h(\delta-1)}\frac{\delta^n}{n!}d\delta \\ &= \frac{1}{\varsigma_s}h^{n+1}\int_0^1 e^{h(\delta-1)}\frac{\delta^n}{n!}d\delta \\ &=: \frac{1}{\varsigma_s}h^{n+1}\psi_{n+1}(h) \\ \end{align}

\(\psi(h)\)は逐次的に以下のように求めることができ、\(\psi_n(h)=\phi_n(-h)\)となる。

\begin{align} \psi_n(h) &= \int_0^1 e^{h(\delta-1)}\frac{\delta^{n-1}}{(n-1)!}d\delta \\ &= \left[\frac{1}{h}e^{h(\delta-1)}\frac{\delta^{n-1}}{(n-1)!}\right]_0^1 - \frac{1}{h}\int_0^1 e^{h(\delta-1)}\frac{\delta^{n-2}}{(n-2)!}d\delta \\ &= \frac{1}{h}\frac{1}{(n-1)!} - \frac{1}{h}\psi_{n-1}(h) \\ &= \frac{1}{h}\frac{1}{(n-1)!} - \frac{1}{h^2}\frac{1}{(n-2)!} + \frac{1}{h^2}\psi_{n-2}(h) \\ &\quad \vdots \\ &= \frac{1}{h}\frac{1}{(n-1)!} - \frac{1}{h^2}\frac{1}{(n-2)!} + \cdots - \frac{(-1)^{n-1}}{h^{n-1}}\frac{1}{1!} + \frac{(-1)^{n-1}}{h^{n-1}}\psi_1(h) \\ &= -\sum_{m=1}^{n-1} \frac{(-1)^{n-m}}{h^{n-m}}\frac{1}{m!} + \frac{(-1)^{n-1}}{h^{n-1}}\int_0^1 e^{h(\delta-1)}\frac{\delta^0}{0!} d\delta \\ &= -\sum_{m=1}^{n-1} \frac{(-1)^{n-m}}{h^{n-m}}\frac{1}{m!} + \frac{(-1)^{n-1}}{h^{n-1}}\frac{1}{h}\left(1-e^{-h}\right) \\ &= -\sum_{m=0}^{n-1} \frac{(-1)^{n-m}}{h^{n-m}}\frac{1}{m!} + \frac{(-1)^n}{h^n}e^{-h} \\ &= \frac{(-1)^n}{h^n} \left( e^{-h} - \sum_{m=0}^{n-1} \frac{(-h)^m}{m!} \right) \\ \end{align}

\(e^{-h}\)のTaylor展開と照らし合わせると、各\(\psi_n(h)\)は次のように表すことができ、全て\(\mathcal{O}(1)\)のオーダーであることがわかる。

\begin{align} \psi_1(h) &= \frac{-1}{h^1}\left( e^{-h} - \sum_{m=0}^{0}\frac{(-h)^m}{m!} \right) = \frac{1}{1!} - \frac{h}{2!} + \frac{h^2}{3!} - \frac{h^3}{4!} + \cdots \\ \psi_2(h) &= \frac{1}{h^2}\left( e^{-h} - \sum_{m=0}^{1}\frac{(-h)^m}{m!} \right) = \frac{1}{2!} - \frac{h}{3!} + \frac{h^2}{4!} - \frac{h^3}{5!} + \cdots \\ \psi_3(h) &= \frac{-1}{h^3}\left( e^{-h} - \sum_{m=0}^{2}\frac{(-h)^m}{m!} \right) = \frac{1}{3!} - \frac{h}{4!} + \frac{h^2}{5!} - \frac{h^3}{6!} + \cdots \\ \vdots \end{align}

積分方程式に戻ると以下を得る。

\begin{align} y_s &= \frac{\varsigma_s}{\varsigma_t}y_t + \varsigma_s\sum_{n=0}^{p-1}\hat{x}_\theta^{(n)}(\lambda_t)\int_{\lambda_s}^{\lambda_t} e^\lambda\frac{(\lambda-\lambda_t)^n}{n!}d\lambda + \varsigma_s\int_{\lambda_s}^{\lambda_t}e^\lambda\mathcal{O}(|\lambda-\lambda_t|^p)d\lambda \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + \varsigma_s\sum_{n=0}^{p-1}\hat{x}_\theta^{(n)}(\lambda_t)\frac{1}{\varsigma_s}h^{n+1}\psi_{n+1}(h) + \mathcal{O}(h^{p+1}) \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + \sum_{n=1}^ph^n\psi_n(h)\hat{x}_\theta^{(n-1)}(\lambda_t) + \mathcal{O}(h^{p+1}) \\ \end{align}

DPM-Solver++

DPM-Solver++ では\(p=1\)までの項を計算する。(収束次数は1)
\(\bar{y}_t-y_t=\mathcal{O}(h^2)\)とすると、\(y_s\)を次のように近似できる。

\begin{align} y_s &= \frac{\varsigma_s}{\varsigma_t}y_t + h^1\psi_1(h)\hat{x}_\theta(\lambda_t) + \mathcal{O}(h^2) \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + (1-e^{-h})x_\theta(y_t) + \mathcal{O}(h^2) \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + (1-\frac{\varsigma_s}{\varsigma_t})\frac{x_t - \sigma_t\varepsilon(y_t)}{\alpha_t} + \mathcal{O}(h^2) \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + (1-\frac{\varsigma_s}{\varsigma_t})\left(y_t-\varsigma_t\varepsilon(y_t)\right) + \mathcal{O}(h^2) \\ &= y_t + (\varsigma_s-\varsigma_t)\varepsilon(y_t) + \mathcal{O}(h^2) \\ &= \bar{y}_t + (\varsigma_s-\varsigma_t)\varepsilon(\bar{y}_t) + \mathcal{O}(h^2) \\ \end{align}

したがって、近似値\(\bar{y}_s\)を次のように定める。

\begin{align} \bar{y}_s &= \bar{y}_t + (\varsigma_s-\varsigma_t)\varepsilon(\bar{y}_t) \end{align}

これはEuler法と全く同じアルゴリズムである。

DPM-Solver++(2S)

DPM-Solver++(2S) では\(p=2\)までの項を計算する。(収束次数は2)

ステップ幅\(kh\)のDPM-Solver++で生成した値\(\bar{y}_r=\bar{y}_{\lambda^{-1}(\lambda_t+kh)}\)を用いて、\(\hat{x}_\theta^{(1)}(\lambda_t)\)を次のように表す。

\begin{align} kh\hat{x}_\theta^{(1)}({\lambda_t}) &= \hat{x}_\theta(\lambda_t+kh) - \hat{x}_\theta(\lambda_t)+ \mathcal{O}(h^2) \\ &= x_\theta(y_r) - x_\theta(y_t)+ \mathcal{O}(h^2) \\ &= x_\theta(\bar{y}_r) + \mathcal{O}(|\bar{y}_r-y_r|) - x_\theta(y_t)+ \mathcal{O}(h^2) \\ &= x_\theta(\bar{y}_r) - x_\theta(y_t) + \mathcal{O}(h^2) \\ \end{align}

\(\bar{y}_t-y_t=\mathcal{O}(h^3)\)とすると、\(y_s\)を以下のように近似できる。

\begin{align} y_s &= \frac{\varsigma_s}{\varsigma_t}y_t + \sum_{n=1}^2h^n\psi_n(h)\hat{x}_\theta^{(n-1)}(\hat{y}_{\lambda_t},{\lambda_t}) + \mathcal{O}(h^3) \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + h\psi_1(h)x_\theta(y_t) + h^2\psi_2(h)\hat{x}_\theta^{(1)}(\hat{y}_{\lambda_t},{\lambda_t}) + \mathcal{O}(h^3) \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + h\psi_1(h)x_\theta(y_t) + \frac{1}{k}\left(\frac{h\psi_1(h)}{2}+\mathcal{O}(h^2)\right)kh\hat{x}_\theta^{(1)}(\hat{y}_{\lambda_t},{\lambda_t}) + \mathcal{O}(h^3) \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + h\psi_1(h)x_\theta(y_t) + \frac{h}{2k}\psi_1(h)\left( x_\theta(\bar{y}_r) - x_\theta(y_t) \right) + \mathcal{O}(h^3) \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + h\psi_1(h)\left( x_\theta(y_t) + \frac{1}{2k}\left( x_\theta(\bar{y}_r) - x_\theta(y_t) \right) \right) + \mathcal{O}(h^3) \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + (1-e^{-h})\left( \left(1-\frac{1}{2k}\right)x_\theta(y_t) + \frac{1}{2k}x_\theta(\bar{y}_r) \right) + \mathcal{O}(h^3) \\ &= \frac{\varsigma_s}{\varsigma_t}\bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( \left(1-\frac{1}{2k}\right)x_\theta(\bar{y}_t) + \frac{1}{2k}x_\theta(\bar{y}_r) \right) + \mathcal{O}(h^3) \\ \end{align}

したがって、近似値\(\bar{y}_s\)を次のように定める。

\begin{align} \bar{y}_s &= \frac{\varsigma_s}{\varsigma_t}\bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( \left(1-\frac{1}{2k}\right)x_\theta(\bar{y}_t) + \frac{1}{2k}x_\theta(\bar{y}_r) \right) \end{align}

\(\varepsilon\)の表記に書き直すと以下のようになる。

\begin{align} \bar{y}_s &= \frac{\varsigma_s}{\varsigma_t}\bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( \left(1-\frac{1}{2k}\right)x_\theta(\bar{y}_t) + \frac{1}{2k}x_\theta(\bar{y}_r) \right) \\ &= \frac{\varsigma_s}{\varsigma_t}\bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( \left(1-\frac{1}{2k}\right)\left( \bar{y}_t-\varsigma_t\varepsilon(\bar{y}_t) \right) + \frac{1}{2k}\left( \bar{y}_r-\varsigma_r\varepsilon(\bar{y}_r) \right) \right) \\ &= \frac{\varsigma_s}{\varsigma_t}\bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( \left(1-\frac{1}{2k}\right)\left( \bar{y}_t-\varsigma_t\varepsilon(\bar{y}_t) \right) + \frac{1}{2k}\left( \bar{y}_t + (\varsigma_r-\varsigma_t)\varepsilon(\bar{y}_t) -\varsigma_r\varepsilon(\bar{y}_r) \right) \right) \\ &= \frac{\varsigma_s}{\varsigma_t}\bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( y_t-\varsigma_t\varepsilon(\bar{y}_t) + \frac{\varsigma_r}{2k}\left( \varepsilon(\bar{y}_t) - \varepsilon(\bar{y}_r) \right) \right) \\ &= \bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( -\varsigma_t\varepsilon(\bar{y}_t) + \frac{\varsigma_r}{2k}\left( \varepsilon(\bar{y}_t) - \varepsilon(\bar{y}_r) \right) \right) \\ &= \bar{y}_t + \left(\varsigma_s-\varsigma_t\right)\left( \varepsilon(\bar{y}_t) + \frac{\varsigma_r}{2k\varsigma_t}\left( \varepsilon(\bar{y}_r)-\varepsilon(\bar{y}_t) \right) \right) \\ &= \bar{y}_t + \left(\varsigma_s-\varsigma_t\right)\left( \varepsilon(\bar{y}_t) + \frac{e^{-kh}}{2k}\left( \varepsilon(\bar{y}_r)-\varepsilon(\bar{y}_t) \right) \right) \\ \end{align}

DPM-Solver-2とよく似ているが、\(r\)に対応する係数が\(\frac{1}{2k}\)から\(\frac{e^{-kh}}{2k}\)に変化しているという違いがある。

DPM-Solver++(2S)のSはSiglestep法を意味し、次に解説するMultistep法と区別するための表記である。
Siglestep法では1つのタイムステップに対して2回モデルを実行する必要がある。

DPM-Solver++(2M)

DPM-Solver++(2M) では、\(s<t<u\)としてタイムステップ\(u\)における既に生成済みの\(\varepsilon(y_u)\)を再利用する。このようにすることで、タイムステップ\(t\)から\(y_s\)を生成するのに\(\varepsilon(y_t)\)の1回分のモデル実行で2次の収束次数を達成できるようになる。このように過去の生成結果を保持しておいて再利用する方法をMultistep法と言う。

DPM-Solver++(2S)のアルゴリズムは以下のようなものだった。

\begin{align} \bar{y}_s &= \frac{\varsigma_s}{\varsigma_t}\bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( \left(1-\frac{1}{2k}\right)x_\theta(\bar{y}_t) + \frac{1}{2k}x_\theta(\bar{y}_r) \right) \\ \end{align}

\(s<t<u\)のとき、\(k\)に負の値を取ることで\(r\)を\(u\)に一致させる。つまり、

\begin{align} \lambda_u &= \lambda_r \\ &= \lambda_t + kh \end{align}

\begin{align} k &= -\frac{\lambda_t-\lambda_u}{h} \\ \end{align}

\(\bar{k}:=-k=\frac{\lambda_t-\lambda_u}{h}\)とする。

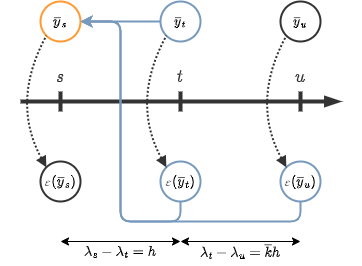
DPM-Solver++(2M)

DPM-Solver++(2S)は以下のように表せる。

\begin{align} \bar{y}_s &= \frac{\varsigma_s}{\varsigma_t}\bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( \left(1+\frac{1}{2\bar{k}}\right)x_\theta(\bar{y}_t) - \frac{1}{2\bar{k}}x_\theta(\bar{y}_u) \right) \\ \end{align}

DPM-Solver++(2M)では2Sのように都度Euler法で\(\bar{y}_u\)を生成するのではなく、既に生成済みの\(\bar{y}_u\)と計算済みの\(x_\theta(\bar{y}_u)\)を再利用する。
\(\bar{y}_u-y_u=\mathcal{O}(h^2)\)であり、\(\varepsilon\)がLipschitz条件を満たすならば、このアルゴリズムもDPM-Solver++(2S)と同様に2次収束する。

\(\varepsilon\)の表記に書き直すと、あまり綺麗にまとまらないが以下のようになる。(2Sとの違いがわかりやすいように項をまとめた)

\begin{align} \bar{y}_s &= \frac{\varsigma_s}{\varsigma_t}\bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( \left(1+\frac{1}{2\bar{k}}\right)x_\theta(\bar{y}_t) - \frac{1}{2\bar{k}}x_\theta(\bar{y}_u) \right) \\ &= \frac{\varsigma_s}{\varsigma_t}\bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( \left(1+\frac{1}{2\bar{k}}\right)(\bar{y}_t-\varsigma_t\varepsilon(\bar{y}_t)) - \frac{1}{2\bar{k}}(\bar{y}_u-\varsigma_u\varepsilon(\bar{y}_u)) \right) \\ &= \frac{\varsigma_s}{\varsigma_t}\bar{y}_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\left( \bar{y}_t + \frac{1}{2\bar{k}}\bar{y}_t - \varsigma_t\varepsilon(\bar{y}_t) - \frac{1}{2\bar{k}}\varsigma_t\varepsilon(\bar{y}_t) - \frac{1}{2\bar{k}}(\bar{y}_u-\varsigma_u\varepsilon(\bar{y}_u)) \right) \\ &= \bar{y}_t + \frac{\varsigma_s-\varsigma_t}{\varsigma_t}\left( \varsigma_t\varepsilon(\bar{y}_t) - \frac{1}{2\bar{k}}\left( \bar{y}_t - \varsigma_t\varepsilon(\bar{y}_t) - \bar{y}_u + \varsigma_u\varepsilon(\bar{y}_u) \right) \right) \\ &= \bar{y}_t + (\varsigma_s-\varsigma_t)\left( \varepsilon(\bar{y}_t) - \frac{1}{2\bar{k}}\left( \frac{\varsigma_u}{\varsigma_t}(\varepsilon(\bar{y}_u)-\varepsilon(\bar{y}_t)) + \frac{\bar{y}_t + (\varsigma_u-\varsigma_t)\varepsilon(\bar{y}_t) - \bar{y}_u}{\varsigma_t} \right) \right) \\ \end{align}

AUTOMATIC1111ではDPM++ 2Mという名前で実装されている。

SDE-DPM-Solver

理論

\(y_t\)に関するSDEは

\begin{align} dy_t &= \sqrt{\frac{d}{dt}\frac{\sigma^2}{\alpha^2}}dw_t \\ &= \sqrt{\frac{d\varsigma_t^2}{dt}}dw_t \\ \end{align}

と表されるので、reverse-time SDEは

\begin{align} dy_t &= \left( 0-\frac{d\varsigma_t^2}{dt} \nabla_{y_t}\log p_t(y_t) \right)dt + \sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &= -\frac{d\varsigma_t^2}{dt} \alpha_t\nabla_{x_t}\log p_t(y_t)dt + \sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &= \frac{d\varsigma_t^2}{dt} \frac{\alpha_t}{\sigma_t}\varepsilon(x_t)dt + \sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &= 2\frac{d\varsigma_t}{dt}\varepsilon(y_t)dt + \sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ \end{align}

となる。
このSDEを\(t\)から\(\lambda\)の表記に書き換える。

\(\lambda_t\)が単調減少であることを考慮して、\(w_\lambda\)を\(s<t\)に対して次のように定める。

\begin{align} w_{\lambda_s} - w_{\lambda_t} \sim \mathcal{N}\left(0, (\lambda_s-\lambda_t)I\right) \end{align}

つまり\(n\sim \mathcal{N}(0,I)\)に対して、

\begin{align} w_{\lambda_s} - w_{\lambda_t} = \sqrt{\lambda_s-\lambda_t}\cdot n \end{align}

が成り立つ。\(s\rightarrow t-dt\)とすると、以下の関係が成り立つことがわかる。

\begin{align} dw_{\lambda_t} &= w_{\lambda_{s-dt}} - w_{\lambda_t} \\ &= \sqrt{\lambda_{s-dt}-\lambda_t}\cdot n \\ &= \sqrt{-\frac{d\lambda_t}{dt}dt}\cdot n \\ &= \sqrt{-\frac{d\lambda_t}{dt}}d\bar{w}_t \\ \end{align}

したがって、reverse-time SDEを\(\lambda_t\)の変数で表すと、

\begin{align} dy_t &= 2\frac{d\varsigma_t}{dt}\varepsilon(y_t)dt + \sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &= 2\frac{d\varsigma_t}{d\lambda_t}\hat{\varepsilon}(\lambda_t)d\lambda_t + \sqrt{\frac{d\varsigma_t^2}{dt}}\frac{1}{\sqrt{-\frac{d\lambda_t}{dt}}}dw_{\lambda_t} \\ &= 2\frac{d\varsigma_t}{d\lambda_t}\hat{\varepsilon}(\lambda_t)d\lambda_t + \sqrt{-\frac{d\varsigma_t^2}{d\lambda_t}}dw_{\lambda_t} \\ &= 2\frac{de^{-\lambda_t}}{d\lambda_t}\hat{\varepsilon}(\lambda_t)d\lambda_t + \sqrt{-\frac{de^{-2\lambda_t}}{d\lambda_t}}dw_{\lambda_t} \\ &= -2e^{-\lambda_t}\hat{\varepsilon}(\lambda_t)d\lambda_t + \sqrt{2e^{-2\lambda_t}}dw_{\lambda_t} \\ &= -2e^{-\lambda_t}\hat{\varepsilon}(\lambda_t)d\lambda_t + \sqrt{2}e^{-\lambda_t}dw_{\lambda_t} \\ \end{align}

となる。
また、このSDEを積分の形で表すと、\(n\sim \mathcal{N}(0,I)\)を用いて以下のようになる。(伊藤積分)

\begin{align} y_s &= y_t - 2 \int_{\lambda_t}^{\lambda_s} e^{-\lambda}\hat{\varepsilon}(\lambda)d\lambda + \sqrt{2\int_{\lambda_t}^{\lambda_s} e^{-2\lambda}d\lambda}\cdot n \\ \end{align}

ここで、

\begin{align} \sqrt{ 2\int_{\lambda_t}^{\lambda_s} e^{-2\lambda} d\lambda } &= \sqrt{ -\left( e^{-2\lambda_s} - e^{-2\lambda_t} \right) } \\ &= \sqrt{ \left(e^{-\lambda_t}\right)^2 - \left( e^{-\lambda_s}\right)^2 } \\ &= \sqrt{\varsigma_t^2-\varsigma_s^2} \\ \end{align}

なので、積分方程式は最終的に以下のようになる。

\begin{align} y_s &= y_t - 2 \int_{\lambda_t}^{\lambda_s} e^{-\lambda}\hat{\varepsilon}(\lambda)d\lambda + \sqrt{\varsigma_t^2-\varsigma_s^2}\cdot n \\ \end{align}

SDE-DPM-Solver-1

\(\hat{\varepsilon}(\lambda)\)をTaylor展開すると、

\begin{align} \hat{\varepsilon}(\hat{y}_\lambda,\lambda) = \varepsilon(y_t) + \mathcal{O}(h) \end{align}

となるので、\(y_s\)は以下のように近似される。

\begin{align} y_s &= y_t - 2 \int_{\lambda_t}^{\lambda_s} e^{-\lambda}\hat{\varepsilon}(\hat{y}_\lambda,\lambda)d\lambda + \sqrt{\varsigma_t^2-\varsigma_s^2}\cdot n \\ &= y_t - 2 \int_{\lambda_t}^{\lambda_s} e^{-\lambda}\left( \varepsilon(y_t) + \mathcal{O}(h) \right)d\lambda + \sqrt{\varsigma_t^2-\varsigma_s^2}\cdot n \\ &= y_t - 2\varepsilon(y_t) \int_{\lambda_t}^{\lambda_s} e^{-\lambda}d\lambda + \sqrt{\varsigma_t^2-\varsigma_s^2}\cdot n + \mathcal{O}(h^2) \\ &= y_t + 2 \left(e^{-\lambda_s}-e^{-\lambda_t}\right)\varepsilon(y_t) + \sqrt{\varsigma_t^2-\varsigma_s^2}\cdot n + \mathcal{O}(h^2) \\ &= y_t + 2 \left(\varsigma_s-\varsigma_t\right)\varepsilon(y_t) + \sqrt{\varsigma_t^2-\varsigma_s^2}\cdot n + \mathcal{O}(h^2) \\ \end{align}

これは、reverse-time SDE

\begin{align} dy_t &= 2\frac{d\varsigma_t}{dt}\varepsilon(y_t)dt + \sqrt{\frac{d\varsigma_t^2}{dt}}d\bar{w}_t \\ &= 2\frac{d\varsigma_t}{dt}\varepsilon(y_t)dt + \sqrt{\frac{d\varsigma_t^2}{dt}dt}\cdot n \\ &= 2\varepsilon(y_t)d\varsigma_t + \sqrt{d\varsigma_t^2}\cdot n \\ &= 2\varepsilon(y_t)d\varsigma_t + \bar{w}_{\varsigma_t} \\ \end{align}

に対する1次近似と考えることも出来る。このような近似をEuler-丸山法と呼ぶ。

SDE-DPM-Solver-2M

SDE-DPM-Solver-2Mでは、\(s<t<u\)としてタイムステップ\(u\)における既に生成済みの\(\varepsilon(y_u)\)を再利用する。

\(s<t<u\)とし、

\begin{align} \begin{cases} h&:=\lambda_s-\lambda_u \\ k&:=\frac{\lambda_t-\lambda_u}{h} \\ \end{cases} \end{align}

と定める。

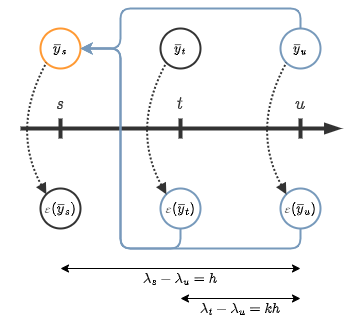
SDE-DPM-Solver++(2M)

\(\lambda\in(\lambda_t,\lambda_s)\)に対して、\(\hat{\varepsilon}(\lambda)\)を次のように近似する。

\begin{align} \hat{\varepsilon}(\lambda) &= \hat{\varepsilon}(\lambda_u) + (\lambda-\lambda_u)\hat{\varepsilon}^{(1)}(\lambda_u) + \mathcal{O}(h^2) \\ &= \hat{\varepsilon}(\lambda_u) + \frac{\lambda-\lambda_u}{\lambda_t-\lambda_u}(\lambda_t-\lambda_u)\hat{\varepsilon}^{(1)}(\lambda_u) + \mathcal{O}(h^2) \\ &= \hat{\varepsilon}(\lambda_u) + \frac{\lambda-\lambda_u}{\lambda_t-\lambda_u}\left( \hat{\varepsilon}(\lambda_t)-\hat{\varepsilon}(\lambda_u) + \mathcal{O}(h^2) \right) + \mathcal{O}(h^2) \\ &= \varepsilon(y_u) + \frac{\lambda-\lambda_u}{\lambda_t-\lambda_u}\left( \varepsilon(y_t)-\varepsilon(y_u) \right) + \mathcal{O}(h^2) \\ \end{align}

積分方程式の積分の部分を計算する。\(\varepsilon\)がLipschitz連続ならば、

\begin{align} -\int_{\lambda_u}^{\lambda_s} e^{-\lambda}\hat{\varepsilon}(\hat{y}_\lambda,\lambda)d\lambda &= -\int_{\lambda_u}^{\lambda_s} e^{-\lambda}\left( \varepsilon(y_u) + \frac{\lambda-\lambda_u}{\lambda_t-\lambda_u}\left( \varepsilon(y_t)-\varepsilon(y_u) \right) + \mathcal{O}(h^2) \right)d\lambda \\ &= \left[ e^{-\lambda}\left( \varepsilon(y_u) + \frac{\lambda-\lambda_u}{\lambda_t-\lambda_u}\left( \varepsilon(y_t)-\varepsilon(y_u) \right) \right) \right]_{\lambda_u}^{\lambda_s} - \int_{\lambda_u}^{\lambda_s} e^{-\lambda}\frac{1}{\lambda_t-\lambda_u}\left( \varepsilon(y_t)-\varepsilon(y_u) \right)d\lambda + \mathcal{O}(h^3) \\ &= \left(e^{-\lambda_s}-e^{-\lambda_u}\right)\varepsilon(y_u) + e^{-\lambda_s}\frac{\lambda_s-\lambda_u}{\lambda_t-\lambda_u}\left( \varepsilon(y_t)-\varepsilon(y_u) \right) + \frac{e^{-\lambda_s}-e^{-\lambda_u}}{\lambda_t-\lambda_u}\left( \varepsilon(y_t)-\varepsilon(y_u) \right) + \mathcal{O}(h^3) \\ &= e^{-\lambda_s} \left( \left(1-e^h\right)\varepsilon(y_u) + \frac{h}{kh}\left( \varepsilon(y_t)-\varepsilon(y_u) \right) + \frac{1-e^h}{kh}\left( \varepsilon(y_t)-\varepsilon(y_u) \right) \right) + \mathcal{O}(h^3) \\ &= e^{-\lambda_s} \left( \left(1-e^h\right)\varepsilon(y_u) + \frac{\varepsilon(y_t)-\varepsilon(y_u)}{k}\left( 1+\frac{1-e^h}{h} \right) \right) + \mathcal{O}(h^3) \\ &= e^{-\lambda_s} \left( \left(1-e^h\right)\varepsilon(y_u) + \frac{\varepsilon(y_t)-\varepsilon(y_u)}{k}\left( \frac{1-e^h}{2} + \mathcal{O}(h^2) \right) \right) + \mathcal{O}(h^3) \\ &= e^{-\lambda_s}\left(1-e^h\right) \left( \varepsilon(y_u) + \frac{1}{2k}\left( \varepsilon(y_t)-\varepsilon(y_u) \right) \right) + \mathcal{O}(|\varepsilon(y_t)-\varepsilon(y_u)|)\mathcal{O}(h^2) + \mathcal{O}(h^3) \\ &= \left(\varsigma_s-\varsigma_u\right) \left( \varepsilon(y_u) + \frac{1}{2k}\left( \varepsilon(y_t)-\varepsilon(y_u) \right) \right) + \mathcal{O}(h^3) \\ \end{align}

積分方程式に戻すと、

\begin{align} y_s &= y_u - 2 \int_{\lambda_u}^{\lambda_s} e^{-\lambda}\hat{\varepsilon}(\hat{y}_\lambda,\lambda)d\lambda + e^{-\lambda_u}\sqrt{ 1-e^{-2h} }\cdot n \\ &= y_u + 2\left(\varsigma_s-\varsigma_u\right) \left( \varepsilon(y_u) + \frac{1}{2k}\left( \varepsilon(y_t)-\varepsilon(y_u) \right) \right) + \sqrt{ \varsigma_u^2-\varsigma_s^2 }\cdot n + \mathcal{O}(h^3) \\ \end{align}

となる。

SDE-DPM-Solver++

理論

reverse-time SDEを\(x_\theta\)の表記に書き換える。

\begin{align} dy_t &= -2e^{-\lambda_t}\hat{\varepsilon}(\lambda_t)d\lambda_t + \sqrt{2}e^{-\lambda_t}dw_{\lambda_t} \\ &= -2e^{-\lambda_t}\frac{y_t-\hat{x}_\theta(\lambda_t)}{\varsigma_t}d\lambda_t + \sqrt{2}e^{-\lambda_t}dw_{\lambda_t} \\ &= -2\left( y_t-\hat{x}_\theta(\lambda_t) \right)d\lambda_t + \sqrt{2}e^{-\lambda_t}dw_{\lambda_t} \\ &= -2y_td\lambda_t +2\hat{x}_\theta(\lambda_t)d\lambda_t + \sqrt{2}e^{-\lambda_t}dw_{\lambda_t} \\ \end{align}

変数を置き換えることで、

\begin{align} d(y_te^{2\lambda_t}) &= 2y_te^{2\lambda_t}d\lambda_t + dy_te^{2\lambda_t} \\ &= e^{2\lambda_t}\left( 2y_td\lambda_t -2y_td\lambda_t +2\hat{x}_\theta(\lambda_t)d\lambda_t + \sqrt{2}e^{-\lambda_t}dw_{\lambda_t} \right) \\ &= 2e^{2\lambda_t}\hat{x}_\theta(\lambda_t)d\lambda_t + \sqrt{2}e^{\lambda_t}dw_{\lambda_t} \\ \end{align}

となり、積分で表すと以下のようになる。

\begin{align} y_se^{2\lambda_s} &= y_te^{2\lambda_t} + 2\int_{\lambda_t}^{\lambda_s}e^{2\lambda}\hat{x}_\theta(\hat{y}_\lambda)d\lambda + \sqrt{2\int_{\lambda_t}^{\lambda_s}e^{2\lambda}d\lambda}\cdot n \\ \end{align}

\begin{align} y_s &= y_te^{-2h} + 2e^{-2\lambda_s}\int_{\lambda_t}^{\lambda_s}e^{2\lambda}\hat{x}_\theta(\hat{y}_\lambda)d\lambda + e^{-2\lambda_s}\sqrt{2\int_{\lambda_t}^{\lambda_s}e^{2\lambda}d\lambda}\cdot n \\ \end{align}

ここで、

\begin{align} e^{-2\lambda_s}\sqrt{ 2\int_{\lambda_t}^{\lambda_s} e^{2\lambda} d\lambda } &= e^{-2\lambda_s}\sqrt{ e^{2\lambda_s} - e^{2\lambda_t} } \\ &= \left(e^{-\lambda_s}\right)^2\sqrt{ \left(e^{-\lambda_s}\right)^{-2} - \left(e^{-\lambda_t}\right)^{-2} } \\ &= \varsigma_s^2\sqrt{ \varsigma_s^{-2} - \varsigma_t^{-2} } \\ &= \sqrt{ \varsigma_s^4 \left(\varsigma_s^{-2} - \varsigma_t^{-2}\right) } \\ &= \sqrt{ \frac{\varsigma_s^2}{\varsigma_t^2}(\varsigma_t^2-\varsigma_s^2) } \\ \end{align}

なので、積分方程式は最終的に以下のようになる。

\begin{align} y_s &= y_te^{-2h} + 2e^{-2\lambda_s}\int_{\lambda_t}^{\lambda_s}e^{2\lambda}\hat{x}_\theta(\hat{y}_\lambda)d\lambda + e^{-\lambda_s}\sqrt{ 1-e^{-2h} }\cdot n \\ &= \frac{\varsigma_s^2}{\varsigma_t^2}y_t + 2\varsigma_s^2\int_{\lambda_t}^{\lambda_s}e^{2\lambda}\hat{x}_\theta(\hat{y}_\lambda)d\lambda + \sqrt{ \frac{\varsigma_s^2}{\varsigma_t^2}(\varsigma_t^2-\varsigma_s^2) }\cdot n \\ \end{align}

SDE-DPM-Solver++1

\(\hat{x}_\theta(\lambda)\)をTaylor展開すると、

\begin{align} \hat{x}_\theta(\lambda) = x_\theta(y_t) + \mathcal{O}(h) \end{align}

となるので、積分方程式は以下のように近似される。

\begin{align} y_s &= \frac{\varsigma_s^2}{\varsigma_t^2}y_t + 2\varsigma_s^2\int_{\lambda_t}^{\lambda_s}e^{2\lambda}\hat{x}_\theta(\lambda)d\lambda + \sqrt{ \frac{\varsigma_s^2}{\varsigma_t^2}(\varsigma_t^2-\varsigma_s^2) }\cdot n \\ &= \frac{\varsigma_s^2}{\varsigma_t^2}y_t + 2\varsigma_s^2\int_{\lambda_t}^{\lambda_s}e^{2\lambda}x_\theta(y_t)d\lambda + \sqrt{ \frac{\varsigma_s^2}{\varsigma_t^2}(\varsigma_t^2-\varsigma_s^2) }\cdot n + \mathcal{O}(h^2) \\ &= \frac{\varsigma_s^2}{\varsigma_t^2}y_t + \varsigma_s^2\left(e^{2\lambda_s}-e^{2\lambda_t}\right)x_\theta(y_t) + \sqrt{ \frac{\varsigma_s^2}{\varsigma_t^2}(\varsigma_t^2-\varsigma_s^2) }\cdot n + \mathcal{O}(h^2) \\ &= \frac{\varsigma_s^2}{\varsigma_t^2}y_t + \left(1-\frac{\varsigma_s^2}{\varsigma_t^2}\right)x_\theta(y_t) + \sqrt{ \frac{\varsigma_s^2}{\varsigma_t^2}(\varsigma_t^2-\varsigma_s^2) }\cdot n + \mathcal{O}(h^2) \\ \end{align}

\(\varepsilon\)の表記に書き換えると以下のようになる。

\begin{align} \bar{y}_s &= \frac{\varsigma_s^2}{\varsigma_t^2}\bar{y}_t + \left(1-\frac{\varsigma_s^2}{\varsigma_t^2}\right)x_\theta(\bar{y}_t) + \sqrt{ \frac{\varsigma_s^2}{\varsigma_t^2}(\varsigma_t^2-\varsigma_s^2) }\cdot n \\ &= \frac{\varsigma_s^2}{\varsigma_t^2}\bar{y}_t + \left(1-\frac{\varsigma_s^2}{\varsigma_t^2}\right)\left( \bar{y}_t-\varsigma_t\varepsilon(\bar{y}_t) \right) + \sqrt{ \frac{\varsigma_s^2}{\varsigma_t^2}(\varsigma_t^2-\varsigma_s^2) }\cdot n \\ &= \bar{y}_t + \frac{\varsigma_s^2-\varsigma_t^2}{\varsigma_t}\varepsilon(\bar{y}_t) + \sqrt{ \frac{\varsigma_s^2}{\varsigma_t^2}(\varsigma_t^2-\varsigma_s^2) }\cdot n \\ \end{align}

これはDDPMと同じアルゴリズムである。

SDE-DPM-Solver++(2M)

SDE-DPM-Solver++(2M) は、SDEにMultistep法を適用した2次精度のアルゴリズムである。

\(s<t<u\)とし、

\begin{align} \begin{cases} h&:=\lambda_s-\lambda_u \\ k&:=\frac{\lambda_t-\lambda_u}{h} \\ \end{cases} \end{align}

と定める。
\(\lambda\in(\lambda_t,\lambda_s)\)に対して、\(\hat{x}_\theta(\lambda)\)を次のように近似する。

\begin{align} \hat{x}_\theta(\hat{y}_\lambda) &= \hat{x}_\theta(\lambda_u) + (\lambda-\lambda_u)\hat{x}_\theta^{(1)}(\lambda_u) + \mathcal{O}(h^2) \\ &= \hat{x}_\theta(\lambda_u) + \frac{\lambda-\lambda_u}{\lambda_t-\lambda_u}(\lambda_t-\lambda_u)\hat{x}_\theta^{(1)}(\lambda_u) + \mathcal{O}(h^2) \\ &= \hat{x}_\theta(\lambda_u) + \frac{\lambda-\lambda_u}{\lambda_t-\lambda_u}\left( \hat{x}_\theta(\lambda_t)-\hat{x}_\theta(\lambda_u) + \mathcal{O}(h^2) \right) + \mathcal{O}(h^2) \\ &= x_\theta(y_u) + \frac{\lambda-\lambda_u}{\lambda_t-\lambda_u}\left( x_\theta(y_t)-x_\theta(y_u) \right) + \mathcal{O}(h^2) \\ \end{align}

積分方程式の積分の部分を計算する。\(\varepsilon\)がLipschitz連続ならば、

\begin{align} 2e^{-2\lambda_s}\int_{\lambda_u}^{\lambda_s}e^{2\lambda}\hat{x}_\theta(\hat{y}_\lambda)d\lambda &= 2e^{-2\lambda_s}\int_{\lambda_u}^{\lambda_s}e^{2\lambda}\left( x_\theta(y_u) + \frac{\lambda-\lambda_u}{\lambda_t-\lambda_u}\left( x_\theta(y_t)-x_\theta(y_u) \right) \right)d\lambda \\ &= e^{-2\lambda_s} \left[ e^{2\lambda}\left( x_\theta(y_u) + e^{2\lambda_s}\frac{\lambda-\lambda_u}{\lambda_t-\lambda_u}\left( x_\theta(y_t)-x_\theta(y_u) \right) \right) \right]_{\lambda_u}^{\lambda_s} - e^{-2\lambda_s}\int_{\lambda_u}^{\lambda_s} e^{2\lambda}\frac{1}{\lambda_t-\lambda_u}\left( x_\theta(y_t)-x_\theta(y_u) \right)d\lambda + \mathcal{O}(h^3) \\ &= e^{-2\lambda_s}\left(e^{2\lambda_s}-e^{2\lambda_u}\right)x_\theta(y_u) + \frac{\lambda_s-\lambda_u}{\lambda_t-\lambda_u}\left( x_\theta(y_t)-x_\theta(y_u) \right) - \frac{1}{2}e^{-2\lambda_s}\frac{e^{2\lambda_s}-e^{2\lambda_u}}{\lambda_t-\lambda_u}\left( x_\theta(y_t)-x_\theta(y_u) \right) + \mathcal{O}(h^3) \\ &= \left(1-e^{-2h}\right)x_\theta(y_u) + \frac{1}{k}\left( x_\theta(y_t)-x_\theta(y_u) \right) - \frac{1}{2}\frac{1-e^{-2h}}{kh}\left( x_\theta(y_t)-x_\theta(y_u) \right) + \mathcal{O}(h^3) \\ &= \left(1-e^{-2h}\right)x_\theta(y_u) + \frac{1}{k}\left( 1 - \frac{1-e^{-2h}}{2h} \right)\left( x_\theta(y_t)-x_\theta(y_u) \right) + \mathcal{O}(h^3) \\ &= \left(1-e^{-2h}\right)x_\theta(y_u) + \frac{1}{k}\left(\frac{1-e^{-2h}}{2}+\mathcal{O}(h^2)\right)\left( x_\theta(y_t)-x_\theta(y_u) \right) + \mathcal{O}(h^3) \\ &= \left(1-e^{-2h}\right)\left( x_\theta(y_u) + \frac{1}{2k}\left( x_\theta(y_t)-x_\theta(y_u) \right) \right) + \mathcal{O}(h^3) \\ &= - \frac{\varsigma_s^2-\varsigma_u^2}{\varsigma_u^2}\left( x_\theta(y_u) + \frac{1}{2k}\left( x_\theta(y_t)-x_\theta(y_u) \right) \right) + \mathcal{O}(h^3) \\ \end{align}

積分方程式に戻すと、

\begin{align} y_s &= \frac{\varsigma_s^2}{\varsigma_t^2}y_t + 2\varsigma_s^2\int_{\lambda_t}^{\lambda_s}e^{2\lambda}\hat{x}_\theta(\hat{y}_\lambda)d\lambda + \sqrt{ \frac{\varsigma_s^2}{\varsigma_t^2}(\varsigma_t^2-\varsigma_s^2) }\cdot n \\ &= \frac{\varsigma_s^2}{\varsigma_u^2}y_u - \frac{\varsigma_s^2-\varsigma_u^2}{\varsigma_u^2}\left( x_\theta(y_u) + \frac{1}{2k}\left( x_\theta(y_t)-x_\theta(y_u) \right) \right) + \sqrt{\frac{\varsigma_s^2}{\varsigma_u^2}\left( \varsigma_u^2-\varsigma_s^2 \right) }\cdot n + \mathcal{O}(h^2) \\ \end{align}

となる。
\(\varepsilon\)の表記に変換すると、こちらも綺麗な形にはまとまらないが、

\begin{align} \bar{y}_s &= \frac{\varsigma_s^2}{\varsigma_u^2}\bar{y}_u - \frac{\varsigma_s^2-\varsigma_u^2}{\varsigma_u^2}\left( x_\theta(y_u) + \frac{1}{2k}\left( x_\theta(\bar{y}_t)-x_\theta(\bar{y}_u) \right) \right) + \sqrt{\frac{\varsigma_s^2}{\varsigma_u^2}\left( \varsigma_u^2-\varsigma_s^2 \right) }\cdot n \\ &= \frac{\varsigma_s^2}{\varsigma_u^2}\bar{y}_u - \frac{\varsigma_s^2-\varsigma_u^2}{\varsigma_u^2}\left( \bar{y}_u-\varsigma_u\varepsilon(\bar{y}_u) + \frac{1}{2k}\left( y_t-\varsigma_t\varepsilon(\bar{y}_t)-\bar{y}_u+\varsigma_u\varepsilon(\bar{y}_u) \right) \right) + \sqrt{\frac{\varsigma_s^2}{\varsigma_u^2}\left( \varsigma_u^2-\varsigma_s^2 \right) }\cdot n \\ &= \bar{y}_u + \frac{\varsigma_s^2-\varsigma_u^2}{\varsigma_u}\varepsilon(\bar{y}_u) - \frac{\varsigma_s^2-\varsigma_u^2}{2k_1\varsigma_u^2}\left( \bar{y}_t-\varsigma_t\varepsilon(\bar{y}_t)-\bar{y}_u+\varsigma_u\varepsilon(\bar{y}_u) \right) + \sqrt{\frac{\varsigma_s^2}{\varsigma_u^2}\left( \varsigma_u^2-\varsigma_s^2 \right) }\cdot n \\ \end{align}

となって、SDE-DPM-Solver++1(=DDPM)に項が追加されたような形になっている。

AUTOMATIC1111ではDPM++ 2M SDEという名前で実装されている。

途中の式で、

\begin{align} 1 - \frac{1-e^{-2h}}{2h} = \frac{1-e^{-2h}}{2} + \mathcal{O}(h^2) \end{align}

という変形を用いた部分があるが、この部分は元の\(1 - \frac{1-e^{-2h}}{2h}\)のままでも実行できる。こちらはAUTOMATIC1111ではDPM++ 2M SDE Heunという名前で実装されている。

参考

• [2206.00927] DPM-Solver: A Fast ODE Solver for Diffusion Probabilistic Model Sampling in Around 10 Steps
• [2211.01095] DPM-Solver++: Fast Solver for Guided Sampling of Diffusion Probabilistic Models
• さんぷらーについて - 勾配降下党青年局