拡散モデルのサンプラー (3) - UniPC

この記事では拡散モデルの生成過程で使われるサンプラーの一種であるUniPCについて解説する。
これまでと同様に、SMLDの前提・表記を用いる。

関連記事

目次

UniPC

UniPCはDPM-Solverの考え方を拡張したアルゴリズム。

前提

以下の定義・表記を用いる。

  • \(s=t_{i+1}<t=t_i<t_{i-1}<\cdots<t_{i-p+1}\)
  • \(r_j := t_{i-j} \qquad (j\in\{1,2,\cdots,p-1\})\)
  • \(r_p := t_{i+1}\)
    • したがって、\(s=r_p<t<r_1<\cdots<r_{p-1}\)
  • \(h := \lambda_s-\lambda_t = \lambda_{t_{i+1}} - \lambda_{t_i}\)
  • \(k_j := \frac{\lambda_{r_j}-\lambda_t}{h} \qquad (j\in\{1,2,\cdots,p\})\)
    • したがって、\(k_p=1\)

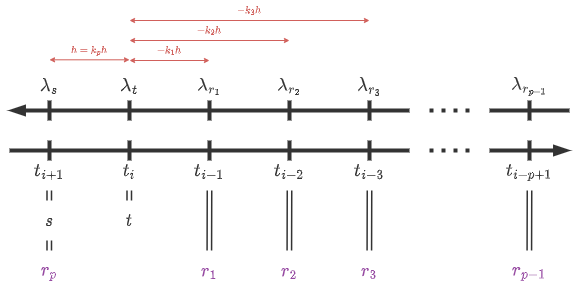
本投稿における表記

UniP

DPM-Solverによると、拡散モデルのODEは

\begin{align} dy_t &= \varepsilon(y_t)d\varsigma_t \\ &= -e^{\lambda_t}\hat{\varepsilon}(\lambda_t)d\lambda_t \\ \end{align}

であり、

\begin{align} y_s &= y_t - \int_{\lambda_t}^{\lambda_s}e^{-\lambda}\hat{\varepsilon}(\lambda)d\lambda \\ &= y_t - \int_{\lambda_t}^{\lambda_s}e^{-\lambda}\sum_{n=0}^{p-1} \frac{(\lambda-\lambda_t)^n}{n!}\hat{\varepsilon}^{(n)}(\lambda_t)d\lambda + \mathcal{O}(h^{p+1}) \\ &= y_t - \varsigma_s\sum_{n=0}^{p-1} h^{n+1}\phi_{n+1}(h)\hat{\varepsilon}^{(n)}(\lambda_t) + \mathcal{O}(h^{p+1}) \\ &= y_t - \varsigma_s(e^h-1)\hat{\varepsilon}(y_t) - \varsigma_s\sum_{n=1}^{p-1} h^{n+1}\phi_{n+1}(h)\hat{\varepsilon}^{(n)}(\lambda_t) + \mathcal{O}(h^{p+1}) \\ &= y_t + (\varsigma_s - \varsigma_t)\hat{\varepsilon}(y_t) - \varsigma_s\sum_{n=1}^{p-1} h^{n+1}\phi_{n+1}(h)\hat{\varepsilon}^{(n)}(\lambda_t) + \mathcal{O}(h^{p+1}) \\ \end{align}

が成り立つことを既に解説した。ただし、\(\phi_n(h)=\sum_{m=0}^\infty\frac{h^m}{(n+m)!}\)

既に計算済みの\(\{\varepsilon(y_{r_j})\}_{j=1}^{p-1}\)と\(\varepsilon(y_t)\)を用いて、

\begin{align} \sum_{n=1}^{p-1} h^{n+1}\phi_{n+1}(h)\hat{\varepsilon}^{(n)}(\lambda_t) = \sum_{j=1}^{p-1} u_j(h)\left(\varepsilon(y_{r_j})-\varepsilon(y_t)\right) + \mathcal{O}(h^{p+1}) \end{align}

と表すことを試みる。この条件を満たす関数の集合\(\{u_j\}_{j=1}^{p-1}\)を探す必要がある。

式を変形すると、

\begin{align} \sum_{n=1}^{p-1} h^{n+1}\phi_{n+1}(h)\hat{\varepsilon}^{(n)}(\lambda_t) &= \sum_{j=1}^{p-1} u_j(h)\left(\varepsilon(y_{r_j})-\varepsilon(y_t)\right) + \mathcal{O}(h^{p+1}) \\ &= \sum_{j=1}^{p-1} u_j(h)\left(\hat{\varepsilon}(\lambda_t+k_jh)-\hat{\varepsilon}(\lambda_t)\right) + \mathcal{O}(h^{p+1}) \\ &= \sum_{j=1}^{p-1} u_j(h)\sum_{n=1}^{p-1}\frac{(k_jh)^n}{n!}\hat{\epsilon}^{(n)}(\lambda_t) + \mathcal{O}(h^{p+1}) \\ &= \sum_{n=1}^{p-1}\frac{h^n}{n!}\left( \sum_{j=1}^{p-1} k_j^nu_j(h) \right)\hat{\epsilon}^{(n)}(\lambda_t) + \mathcal{O}(h^{p+1}) \\ \end{align}

なので、各\(n\in\{1,2,\cdots,p-1\}\)に対して、

\begin{align} h^{n+1}\phi_{n+1}(h) = \frac{h^n}{n!} \sum_{j=1}^{p-1} k_j^nu_j(h) + \mathcal{O}(h^{p+1}) \end{align}

\begin{align} n!h\phi_{n+1}(h) = \sum_{j=1}^{p-1} k_j^nu_j(h) + \mathcal{O}(h^{p+1-n}) \end{align}

となれば良い。これはつまり、

\begin{align} h \begin{pmatrix} 1!\phi_2(h) \\ 2!\phi_3(h) \\ \vdots \\ (p-1)!\phi_p(h) \\ \end{pmatrix} = \begin{pmatrix} 1 & 1 & \cdots & 1 \\ k_1 & k_2 & \cdots & k_{p-1} \\ \vdots & \vdots & \ddots & \vdots \\ k_1^{p-2} & k_2^{p-2} & \cdots & k_{p-1}^{p-2} \end{pmatrix} \begin{pmatrix} k_1u_1(h) \\ k_2u_2(h) \\ \vdots \\ k_{p-1}u_{p-1}(h) \\ \end{pmatrix} + \begin{pmatrix} \mathcal{O}(h^p) \\ \mathcal{O}(h^{p-1}) \\ \vdots \\ \mathcal{O}(h^2) \\ \end{pmatrix} \end{align}

となることを意味する。ここで、

\begin{align} V_{p-1} := \begin{pmatrix} 1 & 1 & \cdots & 1 \\ k_1 & k_2 & \cdots & k_{p-1} \\ \vdots & \vdots & \ddots & \vdots \\ k_1^{p-2} & k_2^{p-2} & \cdots & k_{p-1}^{p-2} \end{pmatrix} \end{align}

はVandermonde行列と呼ばれる行列である。

式を解くと、

\begin{align} \begin{pmatrix} k_1u_1(h) \\ k_2u_2(h) \\ \vdots \\ k_{p-1}u_{p-1}(h) \\ \end{pmatrix} = hV_{p-1}^{-1}\left( \begin{pmatrix} 1!\phi_2(h) \\ 2!\phi_3(h) \\ \vdots \\ (p-1)!\phi_p(h) \\ \end{pmatrix} + \begin{pmatrix} \mathcal{O}(h^{p-1}) \\ \mathcal{O}(h^{p-2}) \\ \vdots \\ \mathcal{O}(h) \\ \end{pmatrix} \right) \end{align}

となる。
この式から、各\(u_j(h)\)は\(u_j(h)=\mathcal{O}(h)\)となることがわかる。

各成分の\(\mathcal{O}(h^{p-n})\)の部分はそれぞれそのオーダー以上の任意の関数に置き換えることができるが、特に全て\(0\)とした場合を考え、

\begin{align} \begin{pmatrix} k_1u_1(h) \\ k_2u_2(h) \\ \vdots \\ k_{p-1}u_{p-1}(h) \\ \end{pmatrix} = hV_{p-1}^{-1} \begin{pmatrix} 1!\phi_2(h) \\ 2!\phi_3(h) \\ \vdots \\ (p-1)!\phi_p(h) \\ \end{pmatrix} \end{align}

とすれば良い。

このようにして求められたアルゴリズムをUniP(Unified Predictor)と言う。収束精度は\(p\)となる。


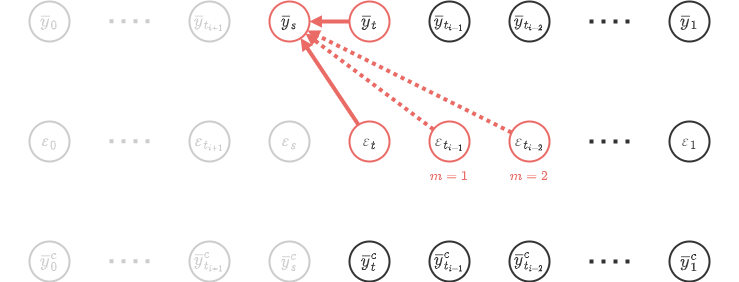
UniP
UniP
  • \(s = t_{i+1}<t = t_i<t_{i-1}<\cdots<t_{i-p+1}\)
  • \(r_j := t_{i-j} \qquad (j\in\{1,2,\cdots,p-1\})\)
  • \(h := \lambda_s - \lambda_t\)
  • \(k_j := \frac{\lambda_{r_j}-\lambda_t}{h} \qquad (j\in\{1,2,\cdots,p-1\})\)
  • \(\{\bar{y}_{r_j}\}_{j=1}^{p-1}\)が既に生成されていて、真の解\(y_{r_j}\)との差が\(\bar{y}_{r_j}-y_{r_j}=\mathcal{O}(h^p)\)
  • \(\bar{y}_t\)が既に生成されていて、真の解\(y_t\)との差が\(\bar{y}_t-y_t=\mathcal{O}(h^{p+1})\)
  • 既に計算済みの\(\{\varepsilon(\bar{y}_{r_j})\}_{j=1}^{p-1}\)と\(\varepsilon(\bar{y}_t)\)を保持している
  • \(\varepsilon_\theta(y_t,t)\)が\(y_t\)に対してLipschitz連続

とする。
このとき、\(\bar{y}_s\)を次のように生成する。

\begin{align} \bar{y}_s = \bar{y}_t + (\varsigma_s - \varsigma_t)\varepsilon(\bar{y}_t) - \varsigma_s\sum_{j=1}^{p-1} \frac{v_j(h)}{k_j}\left(\varepsilon(\bar{y}_{r_j})-\varepsilon(\bar{y}_t)\right) \end{align}

ただし、\(v_j(h)\)は以下から求められる値。

\begin{align} \begin{pmatrix} v_1(h) \\ v_2(h) \\ \vdots \\ v_{p-1}(h) \\ \end{pmatrix} &:= hV_{p-1}^{-1} \begin{pmatrix} 1!\phi_2(h) \\ 2!\phi_3(h) \\ \vdots \\ (p-1)!\phi_p(h) \\ \end{pmatrix} \end{align}

\begin{align} V_{p-1} &:= \begin{pmatrix} 1 & 1 & \cdots & 1 \\ k_1 & k_2 & \cdots & k_{p-1} \\ \vdots & \vdots & \ddots & \vdots \\ k_1^{p-2} & k_2^{p-2} & \cdots & k_{p-1}^{p-2} \end{pmatrix} \end{align}

\begin{align} \phi_n(h) &:= \sum_{m=0}^\infty\frac{h^m}{(n+m)!} \\ &= \frac{1}{h^n}\left( e^h-\sum_{m=0}^{n-1}\frac{h^m}{m!} \right) \end{align}

例 (p=1)

\(p=1\)の場合、総和の項がなくなりEuler法と完全に一致する。

\begin{align} \bar{y}_{t_s} = \bar{y}_t + (\varsigma_s - \varsigma_t)\varepsilon(\bar{y}_t) \end{align}

例 (p=2)

\(p=2\)の場合、行列やベクトルは全て1次元の値になる。

\begin{align} v_1(h) &:= h\cdot1\cdot 1!\phi_2(h) \\ &= \frac{e^h-h-1}{h} \\ \end{align}

となるので、UniPのアルゴリズムは次のようになる。

\begin{align} \bar{y}_{t_s} &= \bar{y}_t + (\varsigma_s - \varsigma_t)\varepsilon(\bar{y}_t) - \varsigma_{t_s}\frac{e^h-h-1}{k_1h}\left(\varepsilon(\bar{y}_{r_1})-\varepsilon(\bar{y}_t)\right) \\ &= \bar{y}_t + (\varsigma_s - \varsigma_t)\left( \varepsilon(\bar{y}_t) + \frac{1}{2k_1}\frac{2(e^h-h-1)}{h(e^h-1)}\left(\varepsilon(\bar{y}_{r_1})-\varepsilon(\bar{y}_t)\right) \right) \\ \end{align}

DPM-Solver-2の導出過程で\(e^h-h-1=\frac{h(e^h-1)}{2}+\mathcal{O}(h^3)\)と近似する場面があるが、その近似を実行しなかった場合に上の式と一致する。

例 (p=3)

\(p=3\)の場合、

\begin{align} \begin{pmatrix} v_1(h) \\ v_2(h) \\ \end{pmatrix} &:= h \begin{pmatrix} 1 & 1 \\ k_1 & k_2 \end{pmatrix}^{-1} \begin{pmatrix} 1!\phi_2(h) \\ 2!\phi_3(h) \\ \end{pmatrix} \\ &= \frac{h}{k_2-k_1} \begin{pmatrix} k_2 & -1 \\ -k_1 & 1 \end{pmatrix} \begin{pmatrix} \phi_2(h) \\ 2\phi_3(h) \\ \end{pmatrix} \\ &= \frac{h}{k_2-k_1} \begin{pmatrix} k_2\phi_2(h)-2\phi_3(h) \\ -k_1\phi_2(h)+2\phi_3(h) \\ \end{pmatrix} \\ \end{align}

となるので、UniPのアルゴリズムは次のようになる。

\begin{align} \bar{y}_{t_s} &= \bar{y}_t + (\varsigma_s - \varsigma_t)\varepsilon(\bar{y}_t) - \varsigma_{t_s}h\frac{k_2\phi_2(h)-2\phi_3(h)}{k_1(k_2-k_1)}\left(\epsilon(\bar{y}_{t_{i-1}})-\varepsilon(\bar{y}_t)\right) - \varsigma_{t_s}h\frac{-k_1\phi_2(h)+2\phi_3(h)}{k_2(k_2-k_1)}\left(\epsilon(\bar{y}_{t_{i-2}})-\varepsilon(\bar{y}_t)\right) \\ \end{align}

UniC

UniPCではUniPに加えて、UniC(Unified Corrector)というアルゴリズムを組み合わせて利用する。
UniCでは、UniPで一旦予測した\(y_s\)を利用して再び\(y_s\)を予測(補正)する。UniPの出力と区別するために、UniCの出力を\(y_s^c\)と表すことにする。

UniCのアルゴリズムの考え方はUniPと全く同じである。UniPでは\(p\)個の値

\begin{align} &\{\varepsilon(y_t), \varepsilon(y_{r_1}), \varepsilon(y_{r_2}), \cdots , \varepsilon(y_{r_{p-1}})\} \\ = &\{\varepsilon(y_t), \varepsilon(y_{t_{i-1}}), \varepsilon(y_{t_{i-2}}), \cdots , \varepsilon(y_{t_{i-p+1}})\} \end{align}

を利用していたが、UniCでは\(p+1\)個の値

\begin{align} &\{\varepsilon(y_t), \varepsilon(y_{r_1}), \varepsilon(y_{r_2}), \cdots , \varepsilon(y_{r_{p-1}}), \varepsilon(y_{r_p})\} \\ = &\{\varepsilon(y_t), \varepsilon(y_{t_{i-1}}), \varepsilon(y_{t_{i-2}}), \cdots , \varepsilon(y_{t_{i-p+1}}), \varepsilon(y_{t_{i+1}})\} \end{align}

を利用して\(p\)個の関数\(v_j(h)\)を求める。

総和の個数が1つ増えたことで、最終的な収束次数は\(p+1\)になる。


UniC
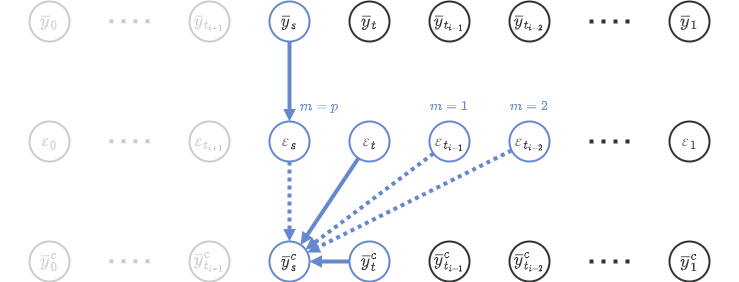
UniC
  • \(s = t_{i+1}<t = t_i<t_{i-1}<\cdots<t_{i-p+1}\)
  • \(r_j := t_{i-j} \qquad (j\in\{1,2,\cdots,p-1\})\)
  • \(r_p := t_{i+1}\)
  • \(h := \lambda_s - \lambda_t\)
  • \(k_j := \frac{\lambda_{r_j}-\lambda_t}{h} \qquad (j\in\{1,2,\cdots,p\})\)
  • \(\{\bar{y}_{r_j}\}_{j=-1}^p\)が既に生成されていて、真の解\(y_{r_j}\)との差が\(\bar{y}_{r_j}-y_{r_j}=\mathcal{O}(h^{p+1})\)
  • \(\bar{y}_t\)が既に生成されていて、真の解\(y_t\)との差が\(\bar{y}_t-y_t=\mathcal{O}(h^{p+1})\)
  • \(\bar{y}^c_t\)が既に生成されていて、真の解\(y_t\)との差が\(\bar{y}^c_t-y_t=\mathcal{O}(h^{p+2})\)
  • 既に計算済みの\(\{\varepsilon(\bar{y}_{r_j})\}_{j=1}^p\)と\(\varepsilon(\bar{y}_t)\)を保持している
  • \(\varepsilon_\theta(y_t,t)\)が\(y_t\)に対してLipschitz連続

とする。
このとき、\(\bar{y}^c_s\)を次のように生成する。

\begin{align} \bar{y}^c_s = \bar{y}^c_t + (\varsigma_s - \varsigma_t)\varepsilon(\bar{y}_t) - \varsigma_s\sum_{j=1}^p \frac{v_j(h)}{k_j}\left(\varepsilon(\bar{y}_{r_j})-\varepsilon(\bar{y}_t)\right) \end{align}

ただし、\(v_j(h)\)は以下から求められる値。

\begin{align} \begin{pmatrix} v_1(h) \\ v_2(h) \\ \vdots \\ v_p(h) \\ \end{pmatrix} &:= hV_p^{-1} \begin{pmatrix} 1!\phi_2(h) \\ 2!\phi_3(h) \\ \vdots \\ p!\phi_{p+1}(h) \\ \end{pmatrix} \end{align}

\begin{align} V_p &:= \begin{pmatrix} 1 & 1 & \cdots & 1 \\ k_1 & k_2 & \cdots & k_p \\ \vdots & \vdots & \ddots & \vdots \\ k_1^{p-1} & k_2^{p-1} & \cdots & k_p^{p-1} \end{pmatrix} \end{align}

\begin{align} \phi_n(h) &:= \sum_{m=0}^\infty\frac{h^m}{(n+m)!} \\ &= \frac{1}{h^n}\left( e^h-\sum_{m=0}^{n-1}\frac{h^m}{m!} \right) \end{align}

UniPとUniCを交互に実行することで\(y^c_t\)を生成していくアルゴリズムがUniPCである。

一方、\(y_t\)の予測には必ずしもUniPを使う必要はなく、DPM-Solverなど他のアルゴリズムとUniCを組み合わせることもできる。論文ではUniPCだけでなく、DDIM + UniCやDPM-Solver++(2M) + UniCなどについても実験が行われ、性能が比較されている。

データ予測モデルのUniPC

データ予測モデルのUniPも同様に導出できる。
DPM-Solver++によると、

\begin{align} y_s &= \frac{\varsigma_s}{\varsigma_t}y_t + \varsigma_s\int_{\lambda_s}^{\lambda_t} e^\lambda\hat{x}_\theta(\lambda)d\lambda \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + \sum_{n=0}^{p-1}h^{n+1}\psi_{n+1}(h)\hat{x}_\theta^{(n)}(\lambda_t) + \mathcal{O}(h^{p+1}) \\ &= \frac{\varsigma_s}{\varsigma_t}y_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\hat{x}_\theta(y_t) + \sum_{n=1}^{p-1}h^{n+1}\psi_{n+1}(h)\hat{x}_\theta^{(n)}(\lambda_t) + \mathcal{O}(h^{p+1}) \\ \end{align}

が成り立つ。ただし、\(\psi_n(h)\)は次のように定義される関数。

\begin{align} \psi_n(h) &= \phi_n(-h) \\ &= \sum_{m=0}^\infty\frac{(-h)^m}{(n+m)!} \end{align}

既に計算済みの\(\{x_\theta(y_{r_j})\}_{j=1}^{p-1}\)と\(x_\theta(y_t)\)を用いて、

\begin{align} \sum_{n=1}^{p-1} h^{n+1}\psi_{n+1}(h)\hat{x_\theta}^{(n)}(\lambda_t) = \sum_{j=1}^{p-1} u_j(h)\left(x_\theta(y_{r_j})-x_\theta(y_t)\right) + \mathcal{O}(h^{p+1}) \end{align}

と表すことを試みる。

ノイズ予測モデルの場合と記号が置き換わっただけなので、以降は同様に求めることができる。UniCの導出も同様。

UniP (for data prediction model)
  • \(s = t_{i+1}<t = t_i<t_{i-1}<\cdots<t_{i-p+1}\)
  • \(r_j := t_{i-j} \qquad (j\in\{1,2,\cdots,p-1\})\)
  • \(h := \lambda_s - \lambda_t\)
  • \(k_j := \frac{\lambda_{r_j}-\lambda_t}{h} \qquad (j\in\{1,2,\cdots,p-1\})\)
  • \(\{\bar{y}_{r_j}\}_{j=1}^{p-1}\)が既に生成されていて、真の解\(y_{r_j}\)との差が\(\bar{y}_{r_j}-y_{r_j}=\mathcal{O}(h^p)\)
  • \(\bar{y}_t\)が既に生成されていて、真の解\(y_t\)との差が\(\bar{y}_t-y_t=\mathcal{O}(h^{p+1})\)
  • 既に計算済みの\(\{x_\theta(\bar{y}_{r_j})\}_{j=1}^{p-1}\)と\(x_\theta(\bar{y}_t)\)を保持している
  • \(\varepsilon_\theta(y_t,t)\)が\(y_t\)に対してLipschitz連続

とする。
このとき、\(\bar{y}_s\)を次のように生成する。

\begin{align} \bar{y}_s = \frac{\varsigma_s}{\varsigma_t}y_t + \left(1-\frac{\varsigma_s}{\varsigma_t}\right)\hat{x}_\theta(y_t) + \sum_{j=1}^{p-1} \frac{v_j(h)}{k_j}\left(x_\theta(y_{r_j})-x_\theta(y_t)\right) \end{align}

ただし、\(v_j(h)\)は以下から求められる値。

\begin{align} \begin{pmatrix} v_1(h) \\ v_2(h) \\ \vdots \\ v_{p-1}(h) \\ \end{pmatrix} &:= hV_{p-1}^{-1} \begin{pmatrix} 1!\psi_2(h) \\ 2!\psi_3(h) \\ \vdots \\ (p-1)!\psi_p(h) \\ \end{pmatrix} \end{align}

\begin{align} V_{p-1} &:= \begin{pmatrix} 1 & 1 & \cdots & 1 \\ k_1 & k_2 & \cdots & k_{p-1} \\ \vdots & \vdots & \ddots & \vdots \\ k_1^{p-2} & k_2^{p-2} & \cdots & k_{p-1}^{p-2} \end{pmatrix} \end{align}

\begin{align} \psi_n(h) &:= \sum_{m=0}^\infty\frac{(-h)^m}{(n+m)!} \\ &= \frac{1}{(-h)^n}\left( e^{-h}-\sum_{m=0}^{n-1}\frac{(-h)^m}{m!} \right) \end{align}

参考