拡散モデルのパラメーター化と損失関数
目次
前提
拡散モデルのパラメーター化
拡散過程
\begin{align} x_0 \mapsto x_t = \alpha_t x_0 + \sigma_t \varepsilon \qquad (t\in[0,1]) \end{align}
に対して、既知の関数\(u_t\)から求められる値\(u_t(x_t,x_0)\)によって、
\begin{align} \underset{\theta}{\mathrm{minimize}} \mathbb{E}_{t,x_0,x_t}\left(w_t\left\| u_\theta(x_t,t)-u_t(x_t,x_0) \right\|^2\right) \end{align}
と学習されるニューラルネットワークモデル\(u_\theta(x_t,t)\)について考える。(\(w_t\)は時間ごとの学習の重みパラメーター)
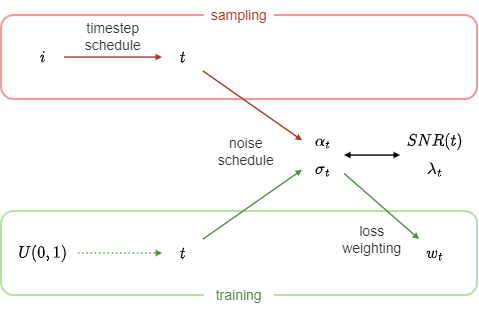
ここでは、\(t\in[0,1]\)は一様分布から取られているものとする。
もし\(t\)が一様分布以外ではなく確率密度\(p(t)\)で表される分布に従う場合、損失関数は\(t\)の一様分布によって次のように表すことができ、分布の差は重みパラメーター\(w_t\)に吸収されることがわかる。
\begin{align} \mathbb{E}_{t\sim p(t),x_0,x_t}\left(w_t\left\| u_\theta(x_t,t)-u_t(x_t,x_0) \right\|^2\right) &= \int_0^1 p(t)\mathbb{E}_{x_0,x_t}\left(w_t\left\| u_\theta(x_t,t)-u_t(x_t,x_0) \right\|^2\right) dt \\ &= \mathbb{E}_{t\sim\mathcal{U}(0,1),x_0,x_t}\left(p(t)w_t\left\| u_\theta(x_t,t)-u_t(x_t,x_0) \right\|^2\right) \end{align}
この問題は、\(u_\theta=\varepsilon_\theta, u_t(x_t,x_0)=\varepsilon=\frac{x_t-\alpha_tx_0}{\sigma_t}\)とすればDDPMやLDMと一致する。
(つまり、この問題はDDPMやLDMなどの既存の拡散モデルをより一般化したものとなっている)
モデルが近似する値
DDPMのときの考察と同様に、
\begin{align} \mathbb{E}_{t,x_0,x_t}\left(w_t\left\| u_\theta(x_t,t)-u_t(x_t,x_0) \right\|^2\right) &= \mathbb{E}_{t,x_0,x_t}\left(w_t \left( \left\|u_\theta(x_t,t)\right\|^2 - 2u_\theta(x_t,t)\cdot u_t(x_t,x_0) + \left\|u_t(x_t,x_0)\right\|^2 \right) \right) \\ &= \mathbb{E}_{t,x_0,x_t}\left(w_t \left( \left\|u_\theta(x_t,t)\right\|^2 - 2u_\theta(x_t,t)\cdot u_t(x_t,x_0) \right) \right) + C \\ &= \mathbb{E}_{t,x_t}\mathbb{E}_{x_0|x_t}\left(w_t \left( \left\|u_\theta(x_t,t)\right\|^2 - 2u_\theta(x_t,t)\cdot u_t(x_t,x_0) \right) \right) + C \\ &= \mathbb{E}_{t,x_t}\left(w_t \left( \left\|u_\theta(x_t,t)\right\|^2 - 2u_\theta(x_t,t)\cdot \mathbb{E}_{x_0|x_t}\left(u_t(x_t,x_0)\right) \right) \right) + C \\ &= \mathbb{E}_{t,x_t}\left(w_t \left\|u_\theta(x_t,t) - \mathbb{E}_{x_0|x_t}\left(u_t(x_t,x_0)\right)\right\|^2 \right) + C \\ \end{align}
となる。(\(C\)は\(\theta\)によらない定数)
したがって、十分学習されたモデルは各\(t,x_t\)ごとに
\begin{align} u_\theta(x_t,t) \sim \mathbb{E}_{x_0|x_t}\left(u_t(x_t,x_0)\right) \end{align}
を推測することになることがわかる。
逆に言えば、\(\mathbb{E}_{x_0|x_t}\left(u_t(x_t,x_0)\right)\)を推測するモデルを学習したいときに、上記の損失関数でその役割を果たせるということになる。本来ならば複雑な確率密度\(p(x_0|x_t)\)による期待値の計算を行って、その値に対する損失関数でモデルを学習する必要があるように思われるが、実は\(x_0\)と\(x_t\)から簡単に計算できる期待値の中身\(u_t(x_t,x_0)\)だけでモデルを学習できるということになる。
パラメーター化・損失の重みの種類
DDPM
DDPMの損失を再び調べる。
\(t=0,1,\cdots,T\)を\(t\in[0,1]\)にスケール変換して表し、\(\Delta t=\frac{1}{T}=\frac{1}{1000}\)とする。
このとき、以前の考察によると、DDPMの損失関数は次のように表される。
\begin{align} Loss &= T\mathbb{E}_{t,x_0,x_t}\left( D_{KL}\left(q(x_{t-\Delta t}|x_t,x_0)\middle\|p_\theta(x_{t-\Delta t}|x_t)\right) \right) \\ &= T\mathbb{E}_{t,x_0,x_t}\left( D_{KL}\left(p_\mathcal{N}(x_{t-\Delta t}|\tilde{\mu}_{t-\Delta t|t}(x_t,x_0),\tilde{\beta}_{t-\Delta t|t})\middle|p_\mathcal{N}(x_{t-\Delta t}|\mu_\theta(x_t,t),\tilde{\beta}_{t-\Delta t|t})\right) \right) \\ &= \mathbb{E}_{t,x_0,x_t}\left( \frac{T}{2\tilde{\beta}_{t-\Delta t|t}} \left\| \mu_\theta(x_t,t) - \tilde{\mu}_{t-\Delta t|t}(x_t,x_0) \right\|^2 \right) \\ \end{align}
ここで、
\begin{align} \tilde{\mu}_{s|t}(x_t,x_0) &= \frac{1}{\sigma_t^2}\left( \alpha_{t|s}\sigma_s^2x_t + \alpha_s\sigma_{t|s}^2x_0 \right) \\ &= \alpha_sx_0 + \sqrt{\sigma_s^2-\tilde{\beta}_{s|t}}\varepsilon \\ &= \frac{1}{\alpha_{t|s}}\left( x_t - \frac{\tilde{\beta}_{s|t}}{\sigma_s^2}\sigma_t\varepsilon \right) \\ \end{align}
\begin{align} \tilde{\beta}_{s|t} &= \frac{\sigma_{t|s}^2\sigma_s^2}{\sigma_t^2} \\ &= \frac{\sigma_s^2}{\sigma_t^2}\left(\sigma_t^2-\frac{\alpha_t^2}{\alpha_s^2}\sigma_s^2\right) \end{align}
である。
このとき、
\begin{align} \tilde{\mu}_{t-\Delta t|t}(x_t,x_0) &= \frac{1}{\alpha_{t|t-\Delta t}}\left( x_t - \frac{\tilde{\beta}_{t-\Delta t|t}}{\sigma_{t-\Delta t}^2}\sigma_t\varepsilon \right) \\ \end{align}
なので、同様に次の式が成立するように\(\varepsilon_\theta(x_t,t)\)を定義する。
\begin{align} \mu_\theta(x_t,x_0) &= \frac{1}{\alpha_{t|t-\Delta t}}\left( x_t - \frac{\tilde{\beta}_{t-\Delta t|t}}{\sigma_{t-\Delta t}^2}\sigma_t\varepsilon_\theta(x_t,t) \right) \\ \end{align}
損失関数を\(\varepsilon\)で表記すると、次のようになる。
\begin{align} Loss &= \mathbb{E}_{t,x_0,x_t}\left( \frac{T}{2\tilde{\beta}_{t-\Delta t|t}} \left\| \mu_\theta(x_t,t) - \tilde{\mu}_{t-\Delta t|t}(x_t,x_0) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{T}{2\tilde{\beta}_{t-\Delta t|t}} \left\| \frac{1}{\alpha_{t|t-\Delta t}}\left( x_t - \frac{\tilde{\beta}_{t-\Delta t|t}}{\sigma_{t-\Delta t}^2}\sigma_t\varepsilon_\theta(x_t,t) \right) - \frac{1}{\alpha_{t|t-\Delta t}}\left( x_t - \frac{\tilde{\beta}_{t-\Delta t|t}}{\sigma_{t-\Delta t}^2}\sigma_t\varepsilon \right) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{T}{2\tilde{\beta}_{t-\Delta t|t}} \left\| \frac{1}{\alpha_{t|t-\Delta t}}\frac{\tilde{\beta}_{t-\Delta t|t}}{\sigma_{t-\Delta t}^2}\sigma_t\left( \varepsilon_\theta(x_t,t) - \varepsilon \right) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{T}{2\tilde{\beta}_{t-\Delta t|t}} \left( \frac{1}{\alpha_{t|t-\Delta t}}\frac{\tilde{\beta}_{t-\Delta t|t}}{\sigma_{t-\Delta t}^2}\sigma_t \right)^2 \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{T}{2}\frac{\alpha_{t-\Delta t}^2}{\alpha_{t}^2}\frac{\sigma_t^2}{\sigma_{t-\Delta t}^2}\frac{\tilde{\beta}_{t-\Delta t|t}}{\sigma_{t-\Delta t}^2} \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{T}{2}\frac{\alpha_{t-\Delta t}^2}{\alpha_{t}^2}\frac{\sigma_t^2}{\sigma_{t-\Delta t}^2}\frac{\frac{\sigma_{t-\Delta t}^2}{\sigma_t^2}\left(\sigma_t^2-\frac{\alpha_t^2}{\alpha_{t-\Delta t}^2}\sigma_{t-\Delta t}^2\right)}{\sigma_{t-\Delta t}^2} \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{T}{2}\frac{\alpha_{t-\Delta t}^2}{\alpha_{t}^2}\frac{\sigma_t^2}{\sigma_{t-\Delta t}^2}\left(1-\frac{\alpha_t^2}{\alpha_{t-\Delta t}^2}\frac{\sigma_{t-\Delta t}^2}{\sigma_t^2}\right) \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{T}{2}\left(\frac{\alpha_{t-\Delta t}^2}{\alpha_t^2}\frac{\sigma_t^2}{\sigma_{t-\Delta t}^2}-1\right) \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
\(\mathrm{SNR}(t):=\alpha_t^2 / \sigma_t^2\)を用いて表すと、
\begin{align} Loss &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{T}{2}\left(\frac{\alpha_{t-\Delta t}^2}{\alpha_t^2}\frac{\sigma_t^2}{\sigma_{t-\Delta t}^2}-1\right) \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{T}{2}\left(\frac{\mathrm{SNR}(t-\Delta t)}{\mathrm{SNR}(t)}-1\right) \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( -\frac{1}{2\mathrm{SNR}(t)}\frac{\mathrm{SNR}(t) - \mathrm{SNR}(t-\Delta t)}{\Delta t} \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &\sim \mathbb{E}_{t,x_0,\varepsilon}\left( -\frac{1}{2\mathrm{SNR}(t)}\mathrm{SNR}'(t) \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( -\frac{1}{2}\left(\log\mathrm{SNR}(t)\right)' \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
となる。
\(\lambda_t:=\log\mathrm{SNR}(t)\)とすると、最終的に損失関数は次のように表される。(DPM-Solverの記事で定義した\(\lambda_t\)とは微妙に異なるので注意)
\begin{align} Loss &\sim \mathbb{E}_{t,x_0,\varepsilon}\left( -\frac{\lambda_t'}{2} \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
DDPMでは次の値を近似するモデルを考える。
\begin{align} \mu_\theta(x_t,t) &\sim \mathbb{E}_{x_0|x_t}\left( \tilde{\mu}_{t-\Delta t|t}(x_t,x_0) \right) \\ &= \mathbb{E}_{x_0|x_t}\left( \frac{1}{\sigma_t^2}\left( \alpha_{t|t-\Delta t}\sigma_{t-\Delta t}^2x_t + \alpha_{t-\Delta t}\sigma_{t|t-\Delta t}^2x_0 \right) \right) \\ &= \mathbb{E}_{x_0|x_t}\left( \alpha_{t-\Delta t}x_0 + \sqrt{\sigma_{t-\Delta t}^2-\tilde{\beta}_{t-\Delta t|t}}\varepsilon(x_t,x_0) \right) \\ \end{align}
損失関数は次のように定義される。
\begin{align} Loss &= \mathbb{E}_{t,x_0,x_t}\left( \frac{T}{2\tilde{\beta}_{t-\Delta t|t}} \left\| \mu_\theta(x_t,t) - \tilde{\mu}_{t-\Delta t|t}(x_t,x_0) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{T}{2}\left(\frac{\mathrm{SNR}(t-\Delta t)}{\mathrm{SNR}(t)}-1\right) \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &\sim \mathbb{E}_{t,x_0,\varepsilon}\left( -\frac{\lambda_t'}{2} \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
DDPM simple (L²-ε)
DDPMでは上記から更に、\(\left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2\)の係数を全て1に正規化した損失関数も提案されている。
\begin{align} Loss &= \mathbb{E}_{t,x_0,\varepsilon}\left( \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
DDPM simpleでは次の値を近似するモデルを考える。
\begin{align} \varepsilon_\theta(x_t,t) &\sim \mathbb{E}_{x_0|x_t}\left( \varepsilon_t(x_t,x_0) \right) \\ &= \mathbb{E}_{x_0|x_t}\left( \frac{x_t-\alpha_tx_0}{\sigma_t} \right) \\ \end{align}
損失関数は次のように定義される。
\begin{align} Loss &= \mathbb{E}_{t,x_0,\varepsilon}\left( \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
L²-μ
DDPM simpleでは損失関数が\(\varepsilon\)の差のL2ノルムで表現された。
それと同じように、\(\mu\)の差のL2ノルムで損失関数を定義した場合を考えてみる。
\begin{align} Loss &= \mathbb{E}_{t,x_0,x_t}\left( \left\| \mu_\theta(x_t,t) - \tilde{\mu}_{t-\Delta t|t}(x_t,x_0) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{2\tilde{\beta}_{t-\Delta t|t}}{T}\frac{T}{2}\left(\frac{\mathrm{SNR}(t-\Delta t)}{\mathrm{SNR}(t)}-1\right) \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \tilde{\beta}_{t-\Delta t|t}\left(\frac{\mathrm{SNR}(t-\Delta t)}{\mathrm{SNR}(t)}-1\right) \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{\sigma_{t-\Delta t}^2}{\sigma_t^2}\left(\sigma_t^2-\frac{\alpha_t^2}{\alpha_{t-\Delta t}^2}\sigma_{t-\Delta t}^2\right)\left(\frac{\mathrm{SNR}(t-\Delta t)}{\mathrm{SNR}(t)}-1\right) \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \sigma_{t-\Delta t}^2\left(1-\frac{\mathrm{SNR}(t)}{\mathrm{SNR}(t-\Delta t)}\right)\left(\frac{\mathrm{SNR}(t-\Delta t)}{\mathrm{SNR}(t)}-1\right) \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \sigma_{t-\Delta t}^2\frac{\left(\mathrm{SNR}(t-\Delta t) - \mathrm{SNR}(t)\right)^2}{\mathrm{SNR}(t)\mathrm{SNR}(t-\Delta t)} \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &\sim \mathbb{E}_{t,x_0,\varepsilon}\left( \left(\Delta t \sigma_t \lambda_t'\right)^2 \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
次の値を近似するモデルを考える。
\begin{align} \mu_\theta(x_t,t) &\sim \mathbb{E}_{x_0|x_t}\left( \tilde{\mu}_{t-\Delta t|t}(x_t,x_0) \right) \\ &= \mathbb{E}_{x_0|x_t}\left( \frac{1}{\sigma_t^2}\left( \alpha_{t|t-\Delta t}\sigma_{t-\Delta t}^2x_t + \alpha_{t-\Delta t}\sigma_{t|t-\Delta t}^2x_0 \right) \right) \\ &= \mathbb{E}_{x_0|x_t}\left( \alpha_{t-\Delta t}x_0 + \sqrt{\sigma_{t-\Delta t}^2-\tilde{\beta}_{t-\Delta t|t}}\varepsilon(x_t,x_0) \right) \\ \end{align}
L²-μの損失関数は次のように定義される。
\begin{align} Loss &= \mathbb{E}_{t,x_0,\varepsilon}\left( \left\| \mu_\theta(x_t,t) - \mu \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \sigma_{t-\Delta t}^2\frac{\left(\mathrm{SNR}(t-\Delta t) - \mathrm{SNR}(t)\right)^2}{\mathrm{SNR}(t)\mathrm{SNR}(t-\Delta t)} \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &\sim \mathbb{E}_{t,x_0,\varepsilon}\left( \left(\Delta t \sigma_t \lambda_t'\right)^2 \left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
DDIM
DDIMの損失関数は次の式で表される。
\begin{align} Loss &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{I}{2}\frac{(\alpha_s-\alpha_tr_t)^2}{s_t^2}\frac{\sigma_t^2}{\alpha_t^2}\|\varepsilon-\varepsilon_\theta(x_t,t)\|^2 \right) \\ \end{align}
ここで、
\begin{align} r_t &= \frac{\sqrt{\sigma_s^2-s_t^2}}{\sigma_t} \\ s_t^2 &= \eta^2\tilde{\beta}_{s|t} \\ \tilde{\beta}_{s|t} &= \frac{\sigma_s^2}{\sigma_t^2}\left(\sigma_t^2-\frac{\alpha_t^2}{\alpha_s^2}\sigma_s^2\right) \\ &= \frac{\sigma_s^2}{\mathrm{SNR}(s)}\left(\mathrm{SNR}(s)-\mathrm{SNR}(t)\right) \end{align}
なので損失関数の重みは、
\begin{align} \frac{I}{2}\frac{(\alpha_s-\alpha_tr_t)^2}{s_t^2}\frac{\sigma_t^2}{\alpha_t^2} &= \frac{I}{2}\frac{\left(\alpha_s-\frac{\alpha_t}{\sigma_t}\sqrt{\sigma_s^2-\eta^2\frac{\sigma_s^2}{\mathrm{SNR}(s)}\left(\mathrm{SNR}(s)-\mathrm{SNR}(t)\right)}\right)^2}{\eta^2\frac{\sigma_s^2}{\mathrm{SNR}(s)}\left(\mathrm{SNR}(s)-\mathrm{SNR}(t)\right)}\frac{1}{\mathrm{SNR}(t)} \\ &= \frac{I}{2\eta^2}\frac{\mathrm{SNR}(s)}{\mathrm{SNR}(t)}\frac{\left(\frac{\alpha_s}{\sigma_s}-\frac{\alpha_t}{\sigma_t}\sqrt{1-\eta^2\frac{\mathrm{SNR}(s)-\mathrm{SNR}(t)}{\mathrm{SNR}(s)}}\right)^2}{\mathrm{SNR}(s)-\mathrm{SNR}(t)} \\ &= \frac{I}{2\eta^2}\frac{\mathrm{SNR}(s)}{\mathrm{SNR}(t)}\frac{\left(\sqrt{\mathrm{SNR}(s)}-\sqrt{\mathrm{SNR}(t)\left( 1-\eta^2\frac{\mathrm{SNR}(s)-\mathrm{SNR}(t)}{\mathrm{SNR}(s)} \right)}\right)^2}{\mathrm{SNR}(s)-\mathrm{SNR}(t)} \\ \end{align}
となる。
ここで、\(x=\mathrm{SNR}(s),a=\mathrm{SNR}(t)\)として、
\begin{align} f(x) &:= \sqrt{x} - \sqrt{a\left(1-\eta^2\frac{x-a}{x}\right)} \\ &= \sqrt{x} - \sqrt{a\left(1-\eta^2\right) + \frac{\eta^2a^2}{x}} \\ g(x) &:= x-a \end{align}
とすると、損失関数の重みは、
\begin{align} \frac{I}{2}\frac{(\alpha_s-\alpha_tr_t)^2}{s_t^2}\frac{\sigma_t^2}{\alpha_t^2} &= \frac{I}{2\eta^2}\frac{\mathrm{SNR}(s)}{\mathrm{SNR}(t)}\frac{\left(\sqrt{\mathrm{SNR}(s)}-\sqrt{\mathrm{SNR}(t)\left( 1-\eta^2\frac{\mathrm{SNR}(s)-\mathrm{SNR}(t)}{\mathrm{SNR}(s)} \right)}\right)^2}{\mathrm{SNR}(s)-\mathrm{SNR}(t)} \\ &= \frac{I}{2\eta^2}\frac{x}{a}\frac{f(x)^2}{g(x)} \\ &= \frac{I}{2\eta^2}\frac{x}{a}\left(\frac{f(x)}{g(x)}\right)^2g(x) \\ \end{align}
と表すことができる。
\(I\rightarrow\infty\)としてこの損失関数を連続化する。
\(\{\tau_i\}_{i=0}^{I}\)が\([0,1]\)から等間隔に選ばれている場合を考える。つまり、\(s=t-\frac{1}{I}\)となるので、\(\Delta t=\frac{1}{I}\)と表すことにする。
このとき、\(x=\mathrm{SNR}(s)=\mathrm{SNR}(t-\Delta t)\rightarrow\mathrm{SNR}(t)=a\)なので、\(f(x)\rightarrow0, g(x)\rightarrow0\)となる。
したがってL'Hôpitalの定理より、
\begin{align} \lim_{x\rightarrow a}\frac{f(x)}{g(x)} &= \lim_{x\rightarrow a}\frac{f'(x)}{g'(x)} \\ &= \lim_{x\rightarrow a}\frac{\frac{1}{2\sqrt{x}}-\frac{-\frac{\eta^2a^2}{x^2}}{2\sqrt{a(1-\eta^2)+\frac{\eta^2a^2}{x}}}}{1} \\ &= \frac{1}{2\sqrt{a}}+\frac{\eta^2}{2\sqrt{a}} \\ &= \frac{1+\eta^2}{2\sqrt{a}} \\ \end{align}
となる。
損失関数の重みは、
\begin{align} \frac{I}{2}\frac{(\alpha_s-\alpha_tr_t)^2}{s_t^2}\frac{\sigma_t^2}{\alpha_t^2} &= \frac{I}{2\eta^2}\frac{x}{a}\left(\frac{f(x)}{g(x)}\right)^2g(x) \\ &\sim \frac{I}{2\eta^2}\frac{x}{a}\left(\frac{1+\eta^2}{2\sqrt{a}}\right)^2g(x) \\ &\sim \frac{(1+\eta^2)^2}{8\eta^2}\frac{1}{a}\frac{g(x)}{\Delta t} \\ &= \frac{(1+\eta^2)^2}{8\eta^2}\frac{1}{\mathrm{SNR}(t)}\frac{\mathrm{SNR}(t-\Delta t)-\mathrm{SNR}(t)}{\Delta t} \\ &\sim \frac{(1+\eta^2)^2}{8\eta^2}\left(-\log\mathrm{SNR}(t)\right)' \\ &= -\frac{(1+\eta^2)^2}{8\eta^2}\lambda_t' \\ \end{align}
となり、\(\eta\)がどんな値を取っても(近似的に)DDPMの損失関数の定数倍になることがわかる。
次の値を近似するモデルを考える。
\begin{align} \varepsilon_\theta(x_t,t) &\sim \mathbb{E}_{x_0|x_t}\left( \varepsilon_t(x_t,x_0) \right) \\ &= \mathbb{E}_{x_0|x_t}\left( \frac{x_t-\alpha_tx_0}{\sigma_t} \right) \\ \end{align}
DDIMの損失関数は次のように定義される。
\begin{align} Loss &= \frac{I}{2\eta^2}\frac{\mathrm{SNR}(s)}{\mathrm{SNR}(t)}\frac{\left(\sqrt{\mathrm{SNR}(s)}-\sqrt{\mathrm{SNR}(t)\left( 1-\eta^2\frac{\mathrm{SNR}(s)-\mathrm{SNR}(t)}{\mathrm{SNR}(s)} \right)}\right)^2}{\mathrm{SNR}(s)-\mathrm{SNR}(t)} \\ &\sim -\frac{(1+\eta^2)^2}{8\eta^2}\lambda_t' \\ \end{align}
L²-x₀
\(x_0=\frac{x_t-\sigma_t\varepsilon}{\alpha_t}\)なので、
\begin{align} x_\theta(x_t,t) := \frac{x_t-\sigma_t\varepsilon_\theta(x_t,t)}{\alpha_t} \end{align}
と定義するモデルは\(x_0\)の近似になることがわかる。
\(x_\theta-x_0\)のL2ノルムを損失関数とすると、次のようになる。
\begin{align} Loss &= \mathbb{E}_{t,x_0,x_t}\left( \left\| x_\theta(x_t,t)-x_0 \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \left\| \frac{x_t-\sigma_t\varepsilon_\theta(x_t,t)}{\alpha_t}-\frac{x_t-\sigma_t\varepsilon}{\alpha_t} \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{\sigma_t^2}{\alpha_t^2}\left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{1}{\mathrm{SNR}(t)}\left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
次の値を近似するモデルを考える。
\begin{align} x_\theta(x_t,t) &\sim \mathbb{E}_{x_0|x_t}\left( x_0 \right) \\ &= \mathbb{E}_{x_0|x_t}\left( \frac{x_t-\sigma_t\varepsilon_t(x_t,x_0)}{\alpha_t} \right) \\ \end{align}
L²-x₀の損失関数は次のように定義される。
\begin{align} Loss &= \mathbb{E}_{t,x_0,x_t}\left( \left\| x_\theta(x_t,t)-x_0 \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{1}{\mathrm{SNR}(t)}\left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
v-prediction
2022年2月にGoogleが発表した論文では、v-predictionと呼ばれる次のようなパラメーター化が提案されている。
\begin{align} v_t(x_t,x_0) &:= \alpha_t\varepsilon - \sigma_tx_0 \\ &= \alpha_t\varepsilon - \sigma_t\frac{x_t-\sigma_t\varepsilon}{\alpha_t} \\ &= -\frac{\sigma_t}{\alpha_t}x_t + \frac{\alpha_t^2+\sigma_t^2}{\alpha_t}\varepsilon \\ v_\theta(x_t,t) &:= -\frac{\sigma_t}{\alpha_t}x_t + \frac{\alpha_t^2+\sigma_t^2}{\alpha_t}\varepsilon_\theta(x_t,t) \\ \end{align}
これは、DDPMでは\(\alpha_t^2+\sigma_t^2=1\)となることから、
\begin{align} \begin{cases} \alpha_t &= \cos(\phi) \\ \sigma_t &= \sin(\phi) \end{cases} \end{align}
と見立て、
\begin{align} x_t&=\alpha_tx_0+\sigma_t\varepsilon \\ &=\cos(\phi)x_0+\sin(\phi)\varepsilon \end{align}
の\(\phi\)による微分を\(v\)と表したものである。
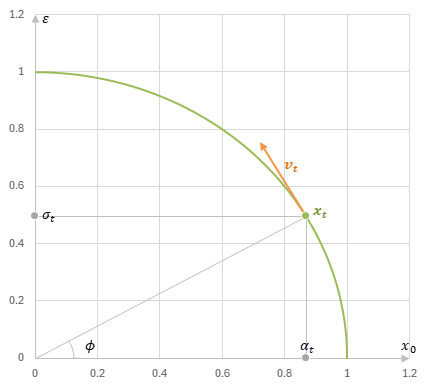
\(v_\theta-v_0\)のL2ノルムを損失関数とすると、次のようになる。
\begin{align} Loss &= \mathbb{E}_{t,x_0,x_t}\left( \left\| v_\theta(x_t,t)-v_t(x_t,x_0) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \left\| (\alpha_t\varepsilon_\theta(x_t,t) - \sigma_tx_0) - (\alpha_t\varepsilon - \sigma_tx_0) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \left\| \left(-\frac{\sigma_t}{\alpha_t}x_t + \frac{\alpha_t^2+\sigma_t^2}{\alpha_t}\varepsilon_\theta(x_t,t)\right) - \left(-\frac{\sigma_t}{\alpha_t}x_t + \frac{\alpha_t^2+\sigma_t^2}{\alpha_t}\varepsilon\right) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{(\alpha_t^2+\sigma_t^2)^2}{\alpha_t^2}\left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
なお、v-predictionでは特に\(\alpha_t=cos\left(\frac{\pi}{2}t\right), \sigma_t=\sqrt{1-\alpha_t^2}\)とするcosineスケジュールが使われる。
次の値を近似するモデルを考える。
\begin{align} v_\theta(x_t,t) &\sim \mathbb{E}_{x_0|x_t}\left( v_t(x_t,x_0) \right) \\ &= \mathbb{E}_{x_0|x_t}\left( \alpha_t\varepsilon_t(x_t,x_0) - \sigma_tx_0 \right) \\ &= \mathbb{E}_{x_0|x_t}\left( \frac{1}{\sigma_t}\left( \alpha_tx_t-(\alpha_t^2+\sigma_t^2)x_0 \right) \right) \\ \end{align}
v-predictionの損失関数は次のように定義される。
\begin{align} Loss &= \mathbb{E}_{t,x_0,x_t}\left( \left\| v_\theta(x_t,t)-v_t(x_t,x_0) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{(\alpha_t^2+\sigma_t^2)^2}{\alpha_t^2}\left\| \varepsilon_\theta(x_t,t) - \varepsilon \right\|^2 \right) \\ \end{align}
NCSN
2019年7月に発表されたNCSN (Noise Conditional Score Network)もこの枠組みの中で考えることができる。
DDPMとは異なり\(\alpha_t=1,\sigma_t=\sigma_\min^{1-t}\sigma_\max^t\)を前提とし、スコアネットワーク\(s_\theta(x_t,t)\)を次の損失関数で学習する。
\begin{align} Loss &= \mathbb{E}_{t,x_0,x_t}\left( \frac{\sigma_t^2}{2}\left\| s_\theta(x_t,t)-\nabla_{x_t}\log p(x_t|x_0) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,x_t}\left( \frac{\sigma_t^2}{2}\left\| s_\theta(x_t,t)-\nabla_{x_t}\log p_\mathcal{N}(x_t|\alpha_tx_0,\sigma_t^2I) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,x_t}\left( \frac{\sigma_t^2}{2}\left\| s_\theta(x_t,t)+\frac{x_t-\alpha_tx_0}{\sigma_t^2} \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{\sigma_t^2}{2}\left\| s_\theta(x_t,t)+\frac{\varepsilon_t(x_t,x_0)}{\sigma_t} \right\|^2 \right) \\ \end{align}
\(s_\theta(x_t,t)=-\frac{\varepsilon_\theta(x_t,t)}{\sigma_t}\)となるように\(\varepsilon_\theta\)を定義することで、損失関数は次のようにも表せる。
\begin{align} Loss &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{\sigma_t^2}{2}\left\| s_\theta(x_t,t)+\frac{\varepsilon_t(x_t,x_0)}{\sigma_t} \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{1}{2}\left\| \varepsilon_\theta(x_t,t)-\varepsilon \right\|^2 \right) \\ \end{align}
これはDDPM simple (L²-ε)の定数倍であり、その差異は学習率によって吸収されるので本質的には同じ損失と言える。
次の値を近似するモデルを考える。
\begin{align} s_\theta(x_t,t) &\sim \nabla_{x_t}\log p(x_t) \\ &= \frac{1}{p(x_t)}\nabla_{x_t} p(x_t) \\ &= \frac{1}{p(x_t)}\nabla_{x_t} \int p(x_0)p(x_t|x_0) dx_0 \\ &= \frac{1}{p(x_t)} \int p(x_0)\nabla_{x_t}p(x_t|x_0) dx_0 \\ &= \frac{1}{p(x_t)} \int p(x_0)p(x_t|x_0)\left( -\frac{x_t-\alpha_tx_0}{\sigma_t^2} \right) dx_0 \\ &= \int p(x_0|x_t)\left( -\frac{x_t-\alpha_tx_0}{\sigma_t^2} \right) dx_0 \\ &= \mathbb{E}_{x_0|x_t}\left( -\frac{x_t-\alpha_tx_0}{\sigma_t^2} \right) \\ &= \mathbb{E}_{x_0|x_t}\left( -\frac{\varepsilon_t(x_t,x_0)}{\sigma_t} \right) \\ \end{align}
NCSNの損失関数は次のように定義される。
\begin{align} Loss &= \mathbb{E}_{t,x_0,x_t}\left( \frac{\sigma_t^2}{2}\left\| s_\theta(x_t,t)-\nabla_x\log p(x_t|x_0) \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left( \frac{1}{2}\left\| \varepsilon_\theta(x_t,t)-\varepsilon \right\|^2 \right) \\ \end{align}
CFM
2022年9月のRectified Flow(RF)や、2022年10月のConditional Flow Matching(CFM)では、次の値を近似するように学習されるモデル\(v_\theta\)が提案された。
\begin{align} v_\theta(x_t,t) \sim \mathbb{E}_{x_0|x_t}\left(\frac{dx_t}{dt}\right) \end{align}
この式は拡散過程と生成過程の2通りの考え方で紐解くことができる。
- 拡散過程として考えたとき
\begin{align} v_\theta(x_t,t) &\sim \mathbb{E}_{x_0|x_t}\left(\frac{dx_t}{dt}\right) \\ &= \mathbb{E}_{x_0|x_t}\left(\frac{d}{dt}(\alpha_tx_0+\sigma_t\epsilon)\right) \\ &= \alpha_t'x_0+\sigma_t'\mathbb{E}_{x_0|x_t}\left(\epsilon\right) \\ &= \alpha_t'\frac{x_t-\sigma_t\varepsilon}{\alpha_t}+\sigma_t'\mathbb{E}_{x_0|x_t}\left(\epsilon\right) \\ &= \frac{\alpha_t'}{\alpha_t}x_t - \sigma_t\left(\frac{\alpha_t'}{\alpha_t}-\frac{\sigma_t'}{\sigma_t}\right)\mathbb{E}_{x_0|x_t}\left(\epsilon\right) \\ &= \frac{\alpha_t'}{\alpha_t}x_t - \sigma_t\frac{d}{dt}\log\frac{\alpha_t}{\sigma_t}\mathbb{E}_{x_0|x_t}\left(\epsilon\right) \\ &= \frac{\alpha_t'}{\alpha_t}x_t - \frac{\sigma_t\lambda_t'}{2}\mathbb{E}_{x_0|x_t}\left(\epsilon\right) \\ \end{align}
- 生成過程として考えたとき、以前の考察から次のようになる。
\begin{align} \frac{dx_t}{dt} &= \frac{\alpha_t'}{\alpha_t}x_t - \frac{1}{2}\alpha_t^2\frac{d}{dt}\left(\frac{\sigma_t^2}{\alpha_t^2}\right)\nabla_x p_t(x_t) \\ &= \frac{\alpha_t'}{\alpha_t}x_t + \frac{1}{2}\alpha_t^2\frac{de^{-\lambda_t}}{dt}\frac{1}{\sigma_t}\mathbb{E}_{x_0|x_t}(\varepsilon_t(x_t,x_0)) \\ &= \frac{\alpha_t'}{\alpha_t}x_t - \frac{1}{2}\frac{\alpha_t^2}{\sigma_t}\lambda_t'e^{-\lambda_t}\mathbb{E}_{x_0|x_t}(\varepsilon_t(x_t,x_0)) \\ &= \frac{\alpha_t'}{\alpha_t}x_t - \frac{\sigma_t\lambda_t'}{2}\mathbb{E}_{x_0|x_t}(\varepsilon_t(x_t,x_0)) \\ \end{align}
したがって、どちらの方法で考えても同じ結果になることがわかる。
\(v_\theta\)はL2ノルムで学習される。
\begin{align} Loss = \mathbb{E}_{t,x_0,\varepsilon}\left(\| v_\theta(x_t,x_0) - \left(\frac{\alpha_t'}{\alpha_t}x_t - \frac{\sigma_t\lambda_t'}{2}\varepsilon\right) \|^2\right) \end{align}
\(v_\theta(x_t,t)=\frac{\alpha_t'}{\alpha_t}x_t - \sigma_t\frac{\lambda_t'}{2}\varepsilon_\theta(x_t,t)\)となるように\(\varepsilon_\theta\)を定義することで、損失関数は次のようにも表せる。
\begin{align} Loss &= \mathbb{E}_{t,x_0,\varepsilon}\left(\| v_\theta(x_t,x_0) - \left(\frac{\alpha_t'}{\alpha_t}x_t - \frac{\sigma_t\lambda_t'}{2}\varepsilon\right) \|^2\right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left(\left(\frac{\sigma_t\lambda_t'}{2}\right)^2\| \varepsilon_\theta(x_t,x_0) - \varepsilon \|^2\right) \\ \end{align}
この損失関数はL²-μで\(\Delta t\sim0\)とした場合の損失の定数倍になっている。
Rectified Flowでは、特に\(\alpha_t,\sigma_t\)は\(\alpha_t=1-t,\sigma_t=t\)と定義される。
このとき、\(\alpha_t'=-1,\sigma_t'=1\)なので、
\begin{align} v_\theta(x_t,t) &\sim \alpha_t'x_0 + \sigma_t'\varepsilon \\ &= \varepsilon-x_0 \\ &= 0\cdot x_0+1\cdot\varepsilon-x_0 \\ &= \alpha_1x_0+\sigma_1\varepsilon-x_0 \\ &= x_1-x_0 \\ \end{align}
となって、損失関数は\(x_0\sim p_{data}\)と\(x_1\sim p_\mathcal{N}(0,I)\)の単純な差で表せることがわかる。
\begin{align} Loss = \mathbb{E}_{t,x_0,\varepsilon}\left(\| v_\theta(x_t,x_0) - (x_1-x_0)) \|^2\right) \\ \end{align}
次の値を近似するモデルを考える。
\begin{align} v_\theta(x_t,t) &\sim \mathbb{E}_{x_0|x_t}\left( \frac{dx_t}{dt} \right) \\ &= \mathbb{E}_{x_0|x_t}\left( \alpha_t'x_0+\sigma_t'\varepsilon_t(x_t,x_0) \right) \\ &= \mathbb{E}_{x_0|x_t}\left( \frac{\sigma_t'}{\sigma_t}x_t - \frac{\alpha_t\lambda_t'}{2}x_0 \right) \\ \end{align}
Rectified Flowの損失関数は次のように定義される。
\begin{align} Loss &= \mathbb{E}_{t,x_0,x_t}\left( \frac{\sigma_t^2}{2}\left\| v_\theta(x_t,t)-\frac{dx_t}{dt} \right\|^2 \right) \\ &= \mathbb{E}_{t,x_0,\varepsilon}\left(\left(\frac{\sigma_t\lambda_t'}{2}\right)^2\| \varepsilon_\theta(x_t,x_0) - \varepsilon \|^2\right) \\ \end{align}
比較
これまでの考察を次の表にまとめる。
損失の重みとはL²-εの形に変形した場合の係数のことであり、定数倍によって表記を揃えてある。
| 名称 | パラメーター化 | 損失の重み |
|---|---|---|
| DDPM | \(\mu_\theta\sim\frac{1}{\sigma_t^2}\left( \alpha_{t|t-\Delta t}\sigma_{t-\Delta t}^2x_t + \alpha_{t-\Delta t}\sigma_{t|t-\Delta t}^2x_0 \right)\) | \(w_t\sim-\lambda_t'\) |
| DDIM | \(\epsilon_\theta\sim\frac{x_t-\alpha_tx_0}{\sigma_t}\) | \(w_t\sim-\lambda_t'\) |
| L²-μ | \(\mu_\theta\sim\frac{1}{\sigma_t^2}\left( \alpha_{t|t-\Delta t}\sigma_{t-\Delta t}^2x_t + \alpha_{t-\Delta t}\sigma_{t|t-\Delta t}^2x_0 \right)\) | \(w_t\sim(\sigma_t\lambda_t')^2\) |
| CFM | \(v_\theta\sim\frac{\sigma_t'}{\sigma_t}x_t - \frac{\alpha_t\lambda_t'}{2}x_0\) | \(w_t=(\sigma_t\lambda_t')^2\) |
| L²-ε | \(\epsilon_\theta\sim\frac{x_t-\alpha_tx_0}{\sigma_t}\) | \(w_t=1\) |
| NCSN | \(s_\theta\sim-\frac{x_t-\alpha_tx_0}{\sigma_t^2}\) | \(w_t=1\) |
| L²-x₀ | \(x_\theta\sim x_0\) | \(w_t=\frac{\sigma_t^2}{\alpha_t^2}\) |
| v-prediction | \(v_\theta\sim\frac{1}{\sigma_t}\left( \alpha_tx_t-(\alpha_t^2+\sigma_t^2)x_0 \right)\) | \(w_t=\frac{(\alpha_t^2+\sigma_t^2)^2}{\alpha_t^2}\) |
noise schedule
これまで確認してきたように、\(\alpha_t,\sigma_t\)の具体的な取り方(=noise schedule=beta schedule)には種類がある。
ここでは、以前紹介した3つ(linear, quadratic linear, cosine)と、NCSN、RFのnoise scheduleを考えることにする。
これらのnoise scheduleからSDEを導出するとき、\(\alpha_t^2+\sigma_t^2=1\)となる最初の3つはVP SDE(分散保存型SDE, Variance Preserving SDE)と呼ばれ、NCSNはVE SDE(分散発散型SDE, Variance Exploding SDE)と呼ばれる。
また、VP-SDEから着想を得て考案されたsub-VP SDEと呼ばれるSDEも存在する。
上に挙げた3つのVP Scheduleそれぞれに対して、それぞれ対応するsub-VP Scheduleについても考えることにする。
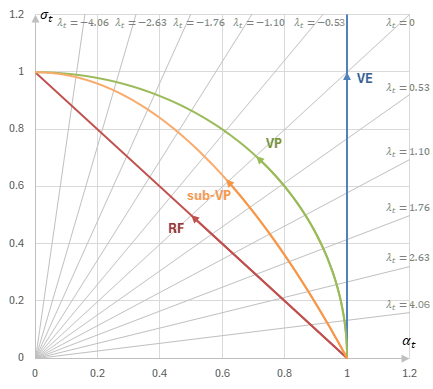
\(\alpha-\sigma\)平面上のnoise schedulerの軌跡
次の表に、それぞれのnoise scheduleの(連続化した)\(\alpha_t,\sigma_t\)の式を示す。
| 名称 | \(\alpha_t\) | \(\sigma_t\) | 備考 |
|---|---|---|---|
| linear | \(\exp\left(-\frac{1}{4a}\left((at+b)^2-b^2\right)\right)\) | \(\sqrt{1-\alpha_t^2}\) | \(a=\frac{1000}{999}(20-0.1)\) \(b=0.1-\frac{20-0.1}{999}\) |
| quadratic linear | \(\exp\left(-\frac{1}{6a}\left((at+b)^3-b^3\right)\right)\) | \(\sqrt{1-\alpha_t^2}\) | \(a=\frac{1000}{999}(\sqrt{12}-\sqrt{0.85})\) \(b=\sqrt{0.85}-\frac{\sqrt{12}-\sqrt{0.85}}{999}\) |
| cosine | \(\cos\left(\frac{\pi}{2}t\right)\) | \(\sqrt{1-\alpha_t^2}=\sin\left(\frac{\pi}{2}t\right)\) | |
| linear (sub-VP) | \(\exp\left(-\frac{1}{4a}\left((at+b)^2-b^2\right)\right)\) | \(1-\alpha_t^2\) | linearと同じ |
| quadratic linear (sub-VP) | \(\exp\left(-\frac{1}{6a}\left((at+b)^3-b^3\right)\right)\) | \(1-\alpha_t^2\) | quadratic linearと同じ |
| cosine (sub-VP) | \(\cos\left(\frac{\pi}{2}t\right)\) | \(1-\alpha_t^2=\sin\left(\frac{\pi}{2}t\right)^2\) | |
| NCSN | \(1\) | \(\sigma_{\min}^{1-t}\sigma_{\max}^t\) | \(\sigma_{\min}=0.1,\sigma_{\max}=10\)など |
| RF | \(1-t\) | \(t\) |
これら8つのnoise scheduleを以下のグラフに示す。
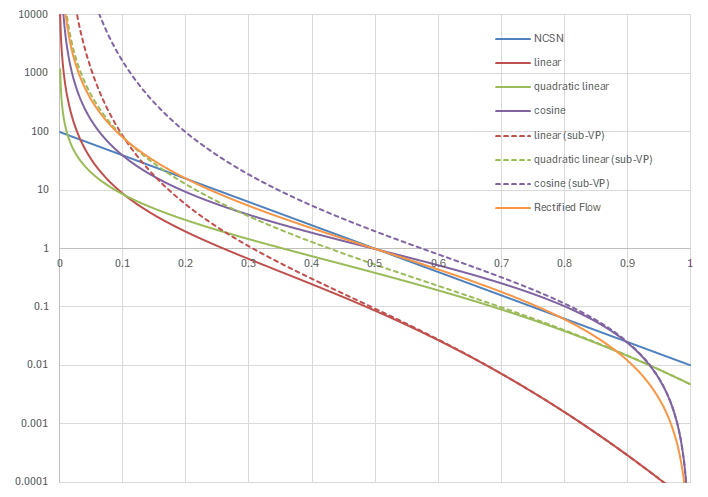
各noise schedulerのSNR (横軸は\(t\), 縦軸は\(\mathrm{SNR}(t)\))
損失の重みの比較
上記の5つのnoise scheduleに対して、それぞれ損失の重みがどのように振る舞うかを見ていく。
以下では\(w_t\)そのものではなく、\(w_t/\lambda_t'\)を計算し最大値が1になるよう正規化した値をグラフに示す。
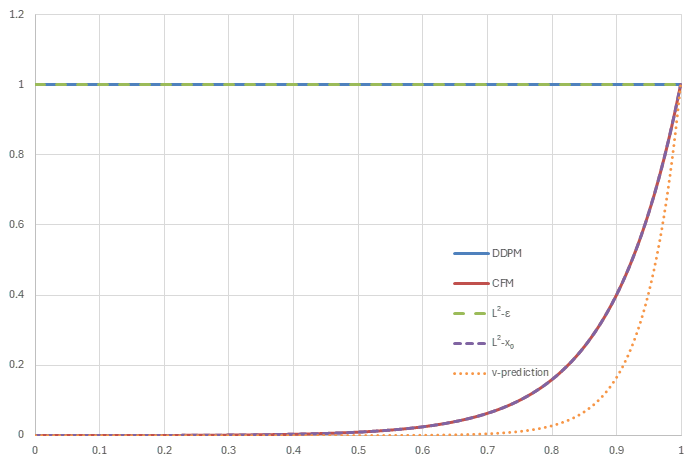
noise schedule=NCSN (横軸はt, 縦軸は正規化された\(w_t/\lambda_t'\))
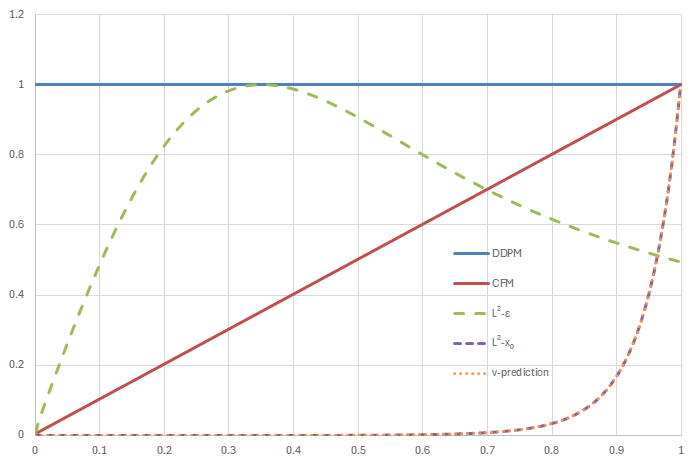
noise schedule=linear (横軸はt, 縦軸は正規化された\(w_t/\lambda_t'\))
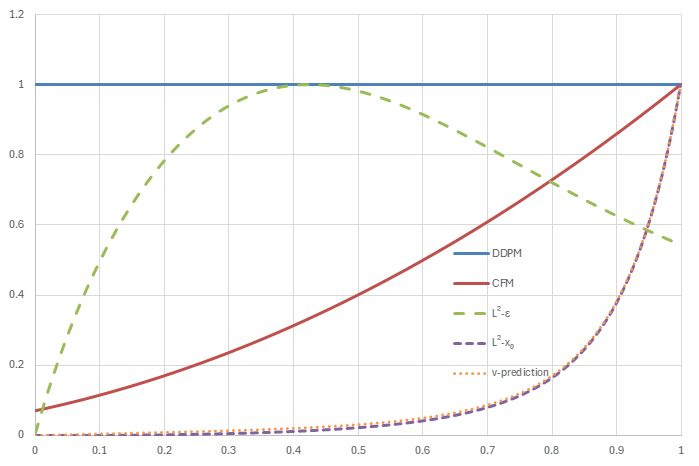
noise schedule=quadratic linear (横軸はt, 縦軸は正規化された\(w_t/\lambda_t'\))
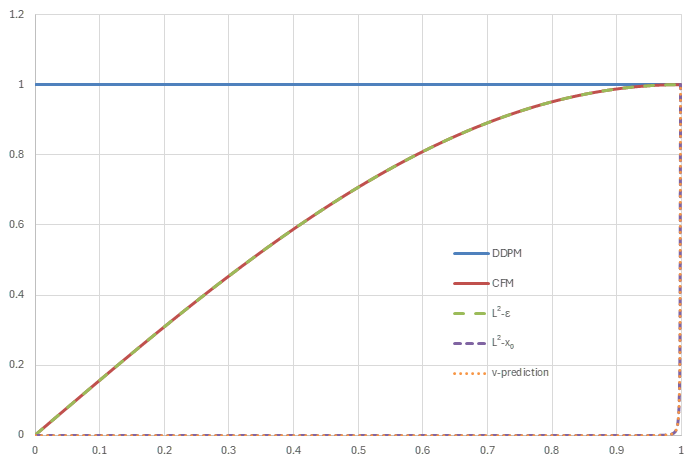
noise schedule=cosine (横軸はt, 縦軸は正規化された\(w_t/\lambda_t'\))
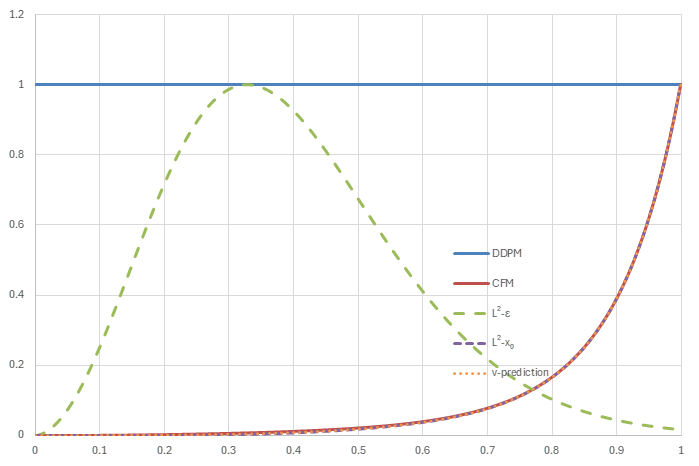
noise schedule=linear (sub-VP) (横軸はt, 縦軸は正規化された\(w_t/\lambda_t'\))
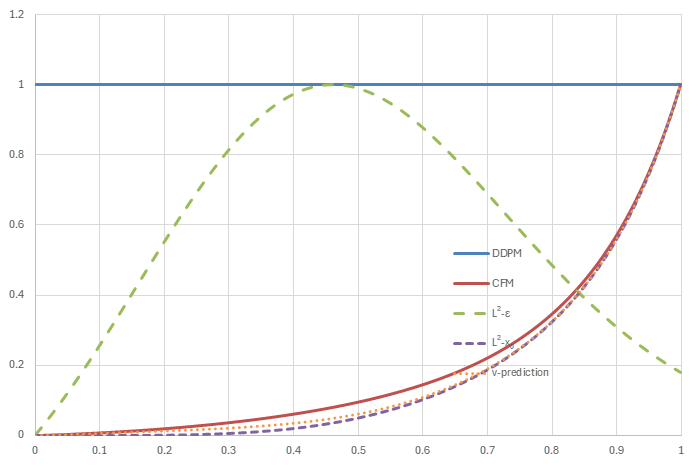
noise schedule=quadratic linear (sub-VP) (横軸はt, 縦軸は正規化された\(w_t/\lambda_t'\))
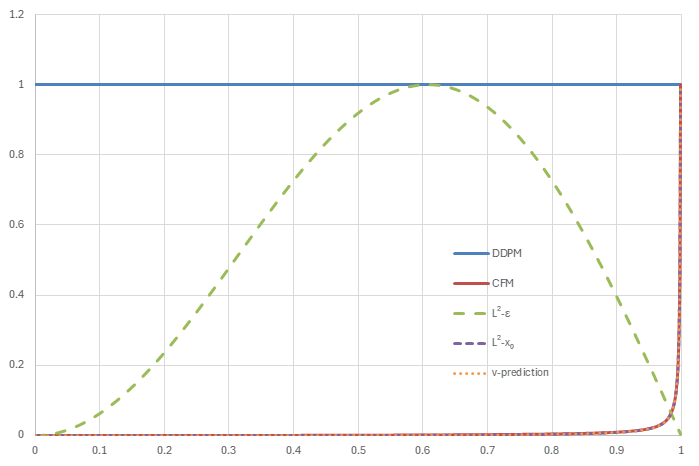
noise schedule=cosine (sub-VP) (横軸はt, 縦軸は正規化された\(w_t/\lambda_t'\))
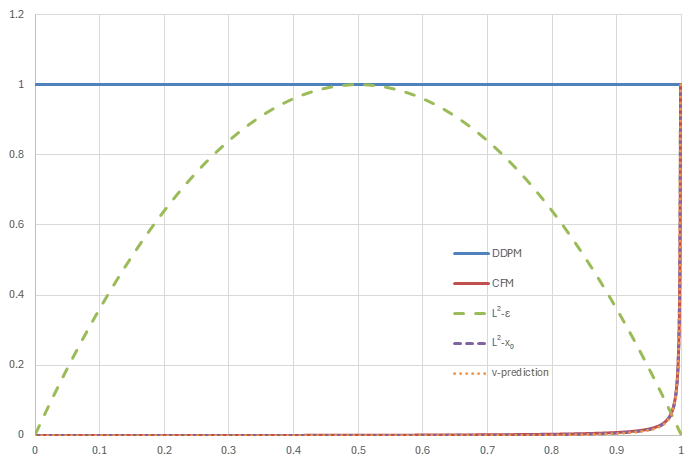
noise schedule=Rectified Flow (横軸はt, 縦軸は正規化された\(w_t/\lambda_t'\))
参考
- [2303.00848] Understanding Diffusion Objectives as the ELBO with Simple Data Augmentation
- [2202.00512] Progressive Distillation for Fast Sampling of Diffusion Models (v-prediction)
- [1907.05600] Generative Modeling by Estimating Gradients of the Data Distribution (NCSN)
- [2209.03003] Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow (Rectified Flow)
- [2302.00482] Improving and generalizing flow-based generative models with minibatch optimal transport (CFM)