Consistency Models

この記事では拡散モデルを高速に実行することのできる技術Consistency Modelsについて解説する。

関連記事

目次

Consistency Models

拡散モデルの生成過程で実行されるサンプラーアルゴリズムの多くは、Probability Flow (PF)に沿ってノイズ\(x_T\)からデータ\(x_0\)を生成する。そのためには、複数回のタイムステップでモデルを実行し、サンプラーの探索軌道を少しずつ修正しながら生成過程を実行しなければならない。

DDPMやLDMで本来1000回必要とされたタイムステップ数は、様々な種類のサンプラーの工夫によって十分な品質を保ちながら数十回程度にまで削減することができるようになったが、それでも依然として拡散モデルの実行の遅さは課題となっていた。


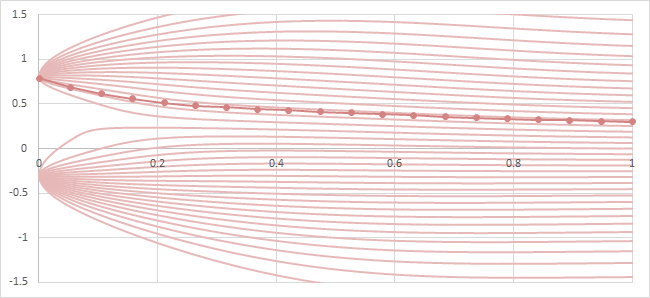
Probability Flowとサンプラーの探索経路の例

2023年3月に発表されたConsistency Models(CM)では拡散モデルをFine-tuneすることで生成過程のステップ数を減らすことを試みた。この研究ではProbability Flow上の一貫性(Consistency)に着目することで、1ステップで直接画像を予測するような学習方法が提案されている。
1ステップ(あるいは4ステップ程度の低ステップ数)でも高品質なデータ(画像)が生成できるようになったことで、拡散モデルを用いた画像のリアルタイム生成も現実的になった。

モデル構造

この理論の目標は任意のタイムステップの入力\(x_t\)に対して、PFに沿った末端の値\(x_0\)を予測するモデル\(f_\theta(x_t,t)\) を構築・学習することである。Consistency Modelsでは、数値的な不安定性を避けるため、\(x_0\)ではなく\(x_\epsilon\)を予測することにする。(\(\epsilon\)は\(0.001\)などの微小な値)

このとき、特にタイムステップ\(\epsilon\)では\(x_\epsilon = f_\theta(x_\epsilon,\epsilon)\)とならなければならず、\(f_\theta(\cdot,\epsilon)\)は恒等写像となる。
この要件を満たすため、\(f_\theta\)を以下のように2つの項で表すことにする。

\begin{align} f_\theta(x,t) = c_{skip}(t)x + c_{out}(t)F_\theta(x,t) \end{align}

ただし、\(c_{skip}(\epsilon)=1, c_{out}(\epsilon)=0\)。\(F_\theta(x,t)\)はニューラルネットワーク。
このようにすることで、\(t=\epsilon\)のときにニューラルネットワークの出力によらず\(x_\epsilon = f_\theta(x_\epsilon,\epsilon)\)が自動的に満たされることになる。


Consistency Modelsの構造

例えばdiffusersの実装では、本論文でも紹介されているKarras氏の研究に従って以下のように定義されている模様。
(\(t\in[0,1]\)とする)

\begin{align} \begin{cases} \sigma_{data} &= 0.5 \\ s &= 10 \\ c_{skip}(t) &= \frac{\sigma_{data}^2}{(sTt)^2+\sigma_{data}^2} \\ c_{out}(t) &= \frac{sTt}{\sqrt{(sTt)^2+\sigma_{data}^2}} \\ F_\theta(x,t) &= x_\theta(x,t) = \frac{x-\sigma_t\varepsilon(x,t)}{\alpha_t} \end{cases} \end{align}

学習

学習は蒸留(Distillation)とFine-tuneの2段階で行われる。

蒸留とは既存の学習済みモデルの入出力を用いて、構造が異なる別のモデルを学習するテクニックである。
本来、蒸留はその名が示すようにモデルを軽量化するための技術であるが、この理論では軽量化ではなく低ステップ数で値を生成するモデルを学習するために既存のモデル(例えばStable DiffusionやSDXL)の入出力を利用する。

Consistency Distillation

Consistency Modelsの蒸留は、同じPFに属する2つの値\(x_t, x_s\)からは同じデータ\(x_0\)が予測されるという前提に基づいて行われる。この前提はself-consistencyと呼ばれ、Consistency Modelsの名前の由来になっている。

同じPFに属する2つの値\(x_t, x_s\)をサンプリングするために教師モデルを用いる。
教師モデルのパラメーターを\(\phi\)と表し、教師モデルを使ったサンプラーを\(Solver_\phi\)と表すことにする。

Consistency Distillationでは、教師データからサンプリングされた\(x_0\)から拡散過程によって\(x_t = \alpha_tx_0+\sigma_t\varepsilon\)を生成し、教師モデルのサンプラーを用いて\(x_t\)から\(x_s\)の近似値\(\bar{x}_s=Solver_\phi(x_t,t\rightarrow s)\)をサンプリングする。


Consistency Distillation (図中の\(y\)は\(x\)に相当し、\(\varsigma\)は\(t\)に相当する)

このようにして得られた\(x_t, \bar{x}_s\)に対して予測されるデータ\(f_\theta(x_t,t), f_\theta(\bar{x}_s,s)\)は、self-consistencyの制約によりほぼ同一の値になっていなければならないので、損失関数を以下のように設計する。

\begin{align} Loss_{x_0,\varepsilon,t,s} = d\left((f_\theta(x_t,t),f_{\theta^-}(\bar{x}_s,s)\right)) \end{align}

ここで、\(d\)は任意の距離関数。論文では\(l^2\)距離・\(l^1\)距離・LPIPSでの性能が比較されている。
また、学習を安定させるために\(\bar{x}_s\)側のモデルのパラメーターにはExponential Moving Average(EMA) \(\theta^-\)が用いられる。EMAは計算グラフからは切断される。(\(\theta\)だけが学習され、\(\theta^-\)側には逆伝播しないということ)

このように学習することで、ノイズが少ないタイムステップ\(s\)とノイズが多いタイムステップ\(t\)で予測される\(x_0\)が一致するようになる。これを様々な\(s,t\)の組み合わせで学習することで、ノイズが多いタイムステップからでも、ノイズが少ないタイムステップからの出力に近い画像\(x_0\)を生成できるようになり、1ステップでの生成が可能となる。

元のConsistency Modelsでは\(s\)は\(t\)の直前のタイムステップとしていたが、それでは学習が遅すぎることがわかり、後述のLCMではより一般に離れたタイムステップ\(s\)も選択することができるSKIPPING-STEPが提案された。

Consistency Distillation
  1. \(x_0\sim p_{data}\)をサンプル。
  2. t,sを選択。
  3. \(x_t\sim\mathcal{N}(\alpha_tx_0,\sigma_t^2I)\)をサンプル。
  4. 教師モデルのサンプラーを用いて、\(\bar{x}_s=Solver_\phi(x_t,t\rightarrow s)\)をサンプル。
  5. \(Loss = d\left(f_\theta(x_t,t),f_{\theta^-}(\bar{x}_s,s)\right)\)を計算。
  6. 損失を逆伝播させてパラメーター\(\theta\)を更新。
    \(\theta\leftarrow\theta-lr\nabla_\theta Loss\)
  7. EMAモデルを更新。
    \(\theta^-\leftarrow\mu\theta^-+(1-\mu)\theta\)

Consistency Training

Fine-tuneでは教師データ\(x_0\)に対して、標準正規分布からサンプリングした同一のノイズ\(\varepsilon\sim\mathcal{N}(0,I)\)を用いて、拡散過程によって\(x_t=\alpha_tx_0+\sigma_t\varepsilon, x_s=\alpha_sx_0+\sigma_s\varepsilon\)をサンプリングする。


Consistency Training

そして、この2つの値を用いてConsistency Distillationと同じように損失を取る。

\begin{align} Loss_{x_0,\varepsilon,t,s} = d\left((f_\theta(x_t,t),f_{\theta^-}(x_s,s)\right)) \end{align}

標準正規ノイズから生成された2つの値\(x_t,x_s\)は同一のPFに属するとは言えないことに注意が必要。

Consistency Training
  1. \(x_0\sim p_{data}\)をサンプル。
  2. t,sを選択。
  3. \(\varepsilon\sim\mathcal{N}(0,I)\)をサンプル。
  4. \(x_t,x_s\)を求める。
    \(x_t:=\alpha_tx_0+\sigma_t\varepsilon\)
    \(x_s:=\alpha_sx_0+\sigma_s\varepsilon\)
  5. \(Loss = d\left(f_\theta(x_t,t),f_{\theta^-}(x_s,s)\right)\)を計算。
  6. 損失を逆伝播させてパラメーター\(\theta\)を更新。
    \(\theta\leftarrow\theta-lr\nabla_\theta Loss\)
  7. EMAモデルを更新。
    \(\theta^-\leftarrow\mu\theta^-+(1-\mu)\theta\)

サンプリング

Consistency Modelsは1ステップでデータ\(x_0\)を予測することを目的としているが、複数ステップで予測することでこれまでの拡散モデルと同様により高品質なサンプリングができることが期待される。
しかし、Consistency Modelsは通常の拡散モデルとは損失関数が全く異なり、これまでのサンプラーで動作するように設計されていない。そのため、後述するLCMでは複数ステップで画像を生成できるように以下のような専用のサンプラーが提案された。

LCM sampler (Multistep Consistency Sampling)

単調増加列\(\tau=\{\tau_0, \tau_1, \tau_2, \cdots , \tau_I\}\subset[0, T]\)を取る。
ただし、\(\tau_I=T, \tau_0=0\)。

  1. \(x_T\in\mathcal{N}(0,I)\)
  2. 以下の手順を\((t,s)=(\tau_I,\tau_{I-1}),(\tau_{I-1},\tau_{I-2}),\cdots,(\tau_2,\tau_1),(\tau_1,\tau_0)\)に対して繰り返し行う。
    1. \(n\sim\mathcal{N}(0,I)\)
    2. \(x_s := \alpha_sf_\theta(x_t,t)+\sigma_sn\)
  3. \(x_0=x_{\tau_0}\)を予測データとして出力。

Multistep Consistency Sampling

サンプラーで大幅にタイムステップを進め、進みすぎたタイムステップ分をノイズによって補正するというこの仕組みはAncestral Samplingによく似ている。上記のサンプラーでは\(t=0\)にまでタイムステップを進めてから戻すので、Ancestral Samplingを最大限に極端にしたものと解釈することができる。

diffusersではこのサンプラーはLCMSchedulerという名前で利用できる。

応用

Latent Consistency Models (LCM)

2023年10月に発表されたLCMは、Consistency ModelsをStable Diffusionのような潜在値の拡散モデルに適用する技術である。前述のSKIPPING-STEPが提案された他、文章入力やCFG Scaleを入力として受け取る構造のモデルが提案された。

教師モデルのサンプラーは\([3, 15]\)の範囲からランダムに選ばれたCFG Scale (\(=\omega+1\))を用いて\(\bar{x}_s\)を生成し、学習対象のLCMモデルは引数としてCFG Scaleを受け取って推論に活用する。

LCMの論文では、Consitency Distillationに相当する学習はLCD(Latent Consistency Distillation)、Consistency Trainingに相当する学習はLCF(Latent Consitency Fine-tuning)と名付けられている。

Dreamshaper v7というSD1.5系のモデルから蒸留されたLCMが論文著者によって公開されている。

LCM-LoRA

2023年11月に発表されたLCM-LoRAは、LCMを「教師モデル」+「LoRA」で学習したものである。
元のモデルからのLoRAによるFine-tuneなので学習が高速・省メモリ・安定である。また、LCM-LoRAと通常のLoRAを組み合わせて活用することができるという利点がある。

LCM-LoRAの学習ではLCDのみを行い、LCFは行っていない模様。
また、教師モデルのサンプラーのCFG Scale (\(=\omega+1\))には8.5などの固定値を用いて学習している。

Stable Diffusion 1.5、SDXL、SSD-1B (SDXLの軽量版)で学習を行ったLoRAが公開されている。

Trajectory Consistency Distillation (TCD)

Consitency Distillationでは\(x_0\)の予測同士で損失関数を取っていたが、2024年2月に発表されたTCDでは\(x_0\)ではなく\(x_r\quad(r<s<t)\)の予測同士で損失関数を取る方法が提案された。

Consistency Modelsでは、\(x_0\)を予測するニューラルネットワーク\(f_\theta\)を、\(c_{skip}(t), c_{out}(t)\)という関数を使って表現していたが、TCDでは拡散モデルからのより自然な定義として次の\(f_\theta\)を用いる。

\begin{align} f_\theta(x_t,t) = x_\theta(x_t,t) = \frac{x_t - \sigma_t\varepsilon_\theta(x_t,t)}{\alpha_t} \end{align}

ニューラルネットワークの出力\(f_\theta(x_t), f_\theta(x_s)\)から\(x_r\)を予測するためにはサンプラーを用いる必要がある。サンプラーには様々な種類があるが、例えばEuler法の場合\(x_r\)の予測値\(f_\theta(x_t,t\rightarrow r)\)は1ステップで次のように求められる。

\begin{align} f_\theta(x_t,t\rightarrow r) &= \frac{\sigma_r}{\sigma_t}x_t - \alpha_r\left(\frac{\sigma_r/\alpha_r}{\sigma_t/\alpha_t}-1\right)x_\theta(x_t,t) \\ &= \frac{\alpha_r}{\alpha_t}x_t - \alpha_r\left(\frac{\sigma_r}{\alpha_r}-\frac{\sigma_t}{\alpha_t}\right)\varepsilon_\theta(x_t,t) \\ \end{align}

また、TCDでは損失関数にL2ノルムを使うので損失関数は次のように表される。

\begin{align} Loss &= \mathbb{E}\left( \| f_\theta(x_t,t\rightarrow r) - f_{\theta^-}(x_s,s\rightarrow r) \|^2 \right) \end{align}

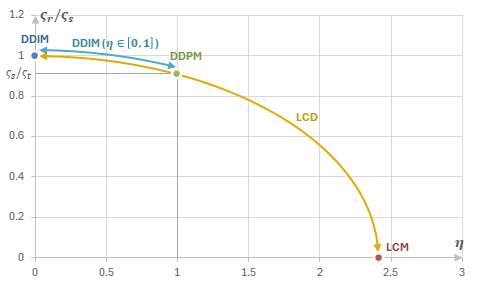
TCDでは\(x_0\)だけでなく中間時刻の\(x_s\)を生成できるので、LCMサンプラーのような特殊な工夫を必要とせずに複数ステップでのサンプリングができる。そこで、新たなサンプラーとして、LCM samplerやAncestral Samplingをパラメーター\(\gamma\)で統一的に表すTCD sampler(γ-sampler)が導入された。
TCD samplerではAncestral Samplingと同様に、「\(x_t\rightarrow x_r\)の予測」・「\(x_r\rightarrow x_s\)のノイズ付与」の2段階で\(x_s\)の生成が実行される。\(r\)はパラメーター\(\gamma\in[0,1]\)で制御され、\(r=(1-\gamma)s\)となる。


Ancestral Sampling

\(\gamma=0\)のときは\(r=s\)なのでDDIM (=Euler)と一致する。
\(\gamma=1\)のときは\(r=0\)なのでLCM samplerと一致する。

TCD sampler (γ-sampler)

単調増加列\(\tau=\{\tau_0, \tau_1, \tau_2, \cdots , \tau_I\}\subset[0, T]\)を取る。
ただし、\(\tau_I=T, \tau_0=0\)。

  1. \(x_T\in\mathcal{N}(0,I)\)
  2. 以下の手順を\((t,s)=(\tau_I,\tau_{I-1}),(\tau_{I-1},\tau_{I-2}),\cdots,(\tau_2,\tau_1),(\tau_1,\tau_0)\)に対して繰り返し行う。
    1. \(r = (1-\gamma)s\)
    2. \(n\sim\mathcal{N}(0,I)\)
    3. \(x_s := \frac{\alpha_s}{\alpha_r}f_\theta(x_t,t\rightarrow r)+\alpha_s\sqrt{\frac{\sigma_s^2}{\alpha_s^2}-\frac{\sigma_r^2}{\alpha_r^2}}\cdot n\)
  3. \(x_0=x_{\tau_0}\)を予測データとして出力。

参考